12.2 Testing a Null Hypothesis with an Exact Approach or Bootstrapping

Exact approaches calculate probabilities for discrete outcomes. In the candy example, the number of yellow candies in a sample bag of ten candies is a discrete outcome. With the binomial formula, the exact probability of zero yellow candies can be calculated, the probability of one yellow candy, two yellow candies, and so on (see Figure 12.2).

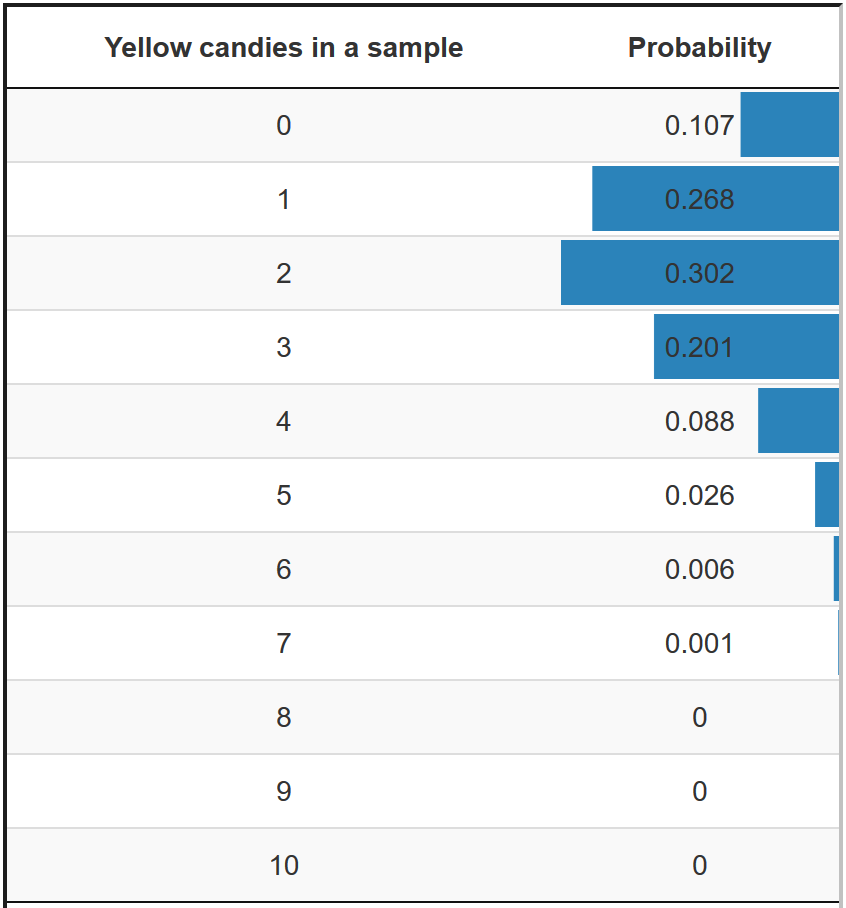
Figure 12.2: Probabilities of a sample with a particular number of yellow candies if 20 per cent of the candies are yellow in the population.

Let us imagine that our sample bag of ten candies contains six yellow candies and we hypothesize that twenty per cent of the candies are yellow in the population. The p value of our sample outcome (six yellow candies) sums the probabilities of drawing a sample bag with six, seven, eight, nine, or ten yellow candies from a population in which twenty per cent of the candies are yellow (our null hypothesis). The p value happens to be (around) .007 (.006 + .001 + 0 + 0 + 0). This is the right-sided p value if we assume that our hypothesis is true.

With the p value, we perform the significance test as usual. The p value is well below the significance level of .05, so we reject the null hypothesis that twenty per cent of all candies in the population are yellow.

The situation is slightly more complicated if we want to execute a significance test with a sampling distribution created with bootstrapping. To understand the testing procedure with bootstrapping, we first have to discuss the relation between null-hypothesis testing and confidence intervals.