10.3 Two Types of Confounders
Figure 10.4: When is a regression effect too large and when is it too small due to a confounder? Numbers represent correlations (lines) or standardized regression coefficients (arrows).
In the preceding section, we learned that a partial effect expressed by a regression coefficient may change if a new predictor is added to the regression model. The partial effect of a predictor changes if the added variable is a confounder: It is correlated both with the predictor and dependent variable. In other words, there is an indirect correlation between the predictor and dependent variable due to the confounding variable.
The partial effect of a predictor can become stronger, weaker, or even change direction if we add a confounder to the regression model. The following sections describe the two types of confounders that are responsible for these changes: suppressors and reinforcers.
10.3.1 Suppression
A predictor’s effect becomes stronger (more strongly positive or more strongly negative) if we include a confounding variable that is responsible for an indirect correlation that points in the opposite direction of the effect of the predictor in the model without the confounder. Here, the indirect correlation contradicts the effect of the predictor and as a result, the effect of the predictor is underestimated (suppressed) if the confounder is not included in the model. The confounder is a suppressor variable. If we add it to the model, it no longer suppresses the effect of the predictor, so this effect becomes stronger.
There are two situations in which an indirect correlation can have the opposite sign of the effect of a predictor:
The indirect correlation is negative but the effect of the predictor is positive.
The indirect correlation is positive but the effect of the predictor is negative.
We start with the first situation and discuss the second situation later on in this section.
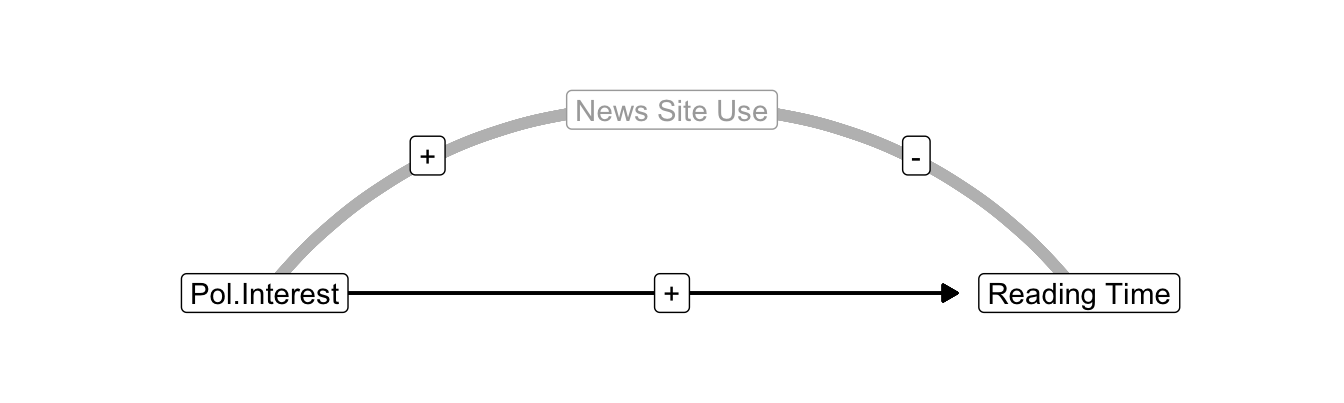
Figure 10.5: News site use as a confounder of the effect of interest in politics on newspaper reading time.
Let us assume that political interest has a positive effect on reading newspapers. People who are more interested in politics tend to spend more time on reading newspapers than people who are less interested in politics. The use of news sites confounds this effect if it is correlated with both political interest and newspaper reading time. What happens if people interested in politics use news sites more often (positive correlation) because they offer the latest political news but using news sites decreases newspaper reading time (negative correlation) because most of the political information has already been provided by the news sites?
In this situation, the indirect correlation between political interest and newspaper reading time due to news site use is negative: Positive times negative yields a negative. The indirect correlation tells us that people interested in politics use news sites more frequently but people who frequently use news sites read newspapers less often. The indirect correlation clearly contradicts the regression effect of political interest on newspaper reading time, which is positive: People who are more interested in politics spend more time on reading newspapers.
If news site use is not included in the regression model, the standardized regression effect of political interest more or less adds the indirect correlation to the effect of political interest. Adding a negative amount (indirect correlation), however, is equal to subtracting this amount from the standardized regression coefficient. The positive effect of political interest on reading time is underestimated. In this example, the effect of political interest is suppressed (masked) by the confounder news site use. News site use is a suppressor variable.
If we include this suppressor variable (news site use) in our regression model, we eliminate its suppression of the effect of political interest on newspaper reading time. The negative effect of news site use on reading time is now captured by the regression coefficient for the news site use predictor. The effect of political interest on newspaper reading time is now controlled for the effect of news site use; it no longer includes the indirect correlation due to news site use. In this example, the effect of political interest on newspaper reading time becomes more strongly positive.
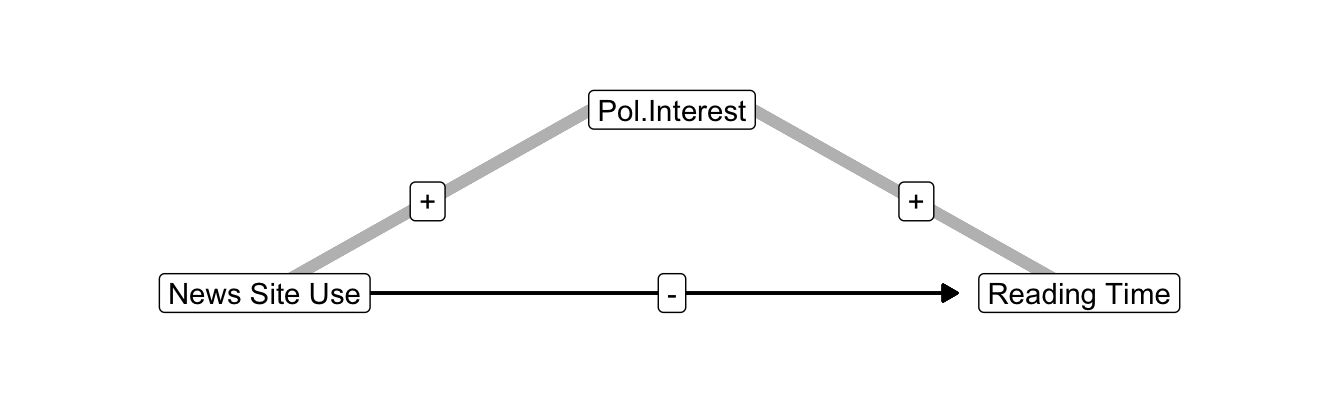
Figure 10.6: Interest in politics as a confounder of the effect of news site use on newspaper reading time.
Now, let us have a look at the situation in which the indirect correlation is positive but the regression effect of the predictor is negative. Just reverse the example and make news site use the predictor and political interest the confounder. The regression effect of news site use on newspaper reading time is negative if people tend to use news sites instead of newspapers as sources of information. The indirect correlation due to political interest, however, is positive if politically interested people use news sites more and spend more time on reading newspapers. In this scenario, the negative effect of news site use on newspaper reading is underestimated if we do not control for political interest.
Suppression can have surprising effects. If the predictor’s original effect was close to zero, adding a suppressor variable to the model will strengthen the effect. An effect that we initially believed to be absent may turn out to be substantial and statistically significant. If our regression model tells us that our predictor does not have an effect, we cannot rule out that it does have an effect that is suppressed by a suppressor variable.
In addition, indirect correlations due to other predictors can add so much to the original partial effect of a predictor that the standardized regression coefficient becomes higher than 1 or lower than -1. This illustrates that standardized regression coefficients are not correlations in multiple regression models because correlations can never be higher than 1 or lower than -1. In contrast, the standardized regression coefficient in a simple regression model is equal to the correlation between predictor and outcome. This is an important difference between simple and multiple regression models.
10.3.2 Reinforcement and spuriousness
Adding a new predictor to a regression model may weaken the effects of other predictors or even change the direction of effects. This happens if the indirect correlation due to a confounder has the same direction (sign) as the regression effect of the predictor in the model without the confounder. Either the indirect correlation and regression effect are both positive or they are both negative.
In both situations, regression effects are initially overestimated because the predictors cover part of the effect of an important variable that has not yet been added to the regression model. The part of the effect that is due to the confounding variable is called spurious. The confounding variable is called a reinforcer because it makes an effect appear more strongly positive or more strongly negative than it really is as long as the confounder has not been added to the regression model.
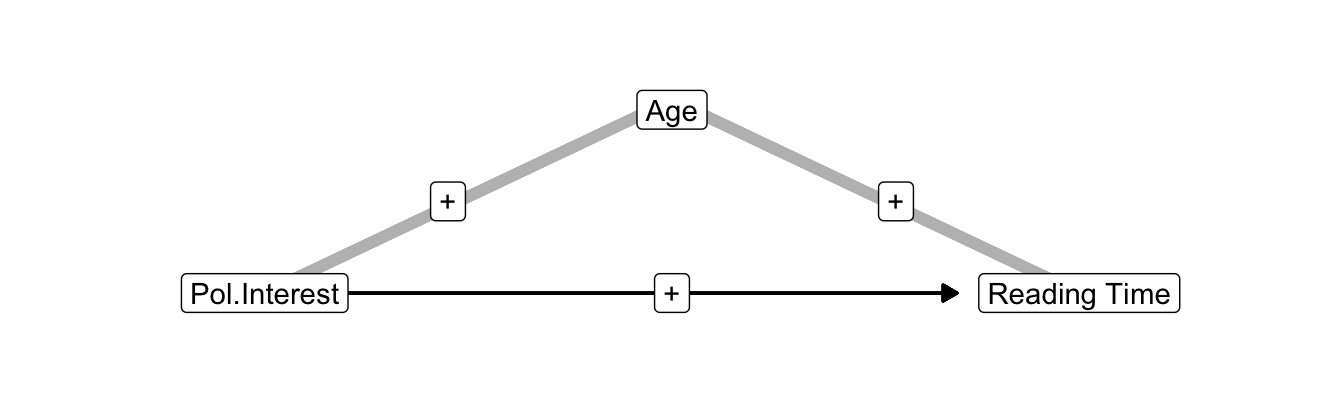
Figure 10.7: Age as a confounder of the effect of interest in politics on newspaper reading time.
As an example, the effect of political interest on newspaper reading time may include the effect of age on newspaper reading when age is not (yet) included in the regression model. If older people are more interested in politics and do more newspaper reading, age creates a positive indirect correlation between political interest and newspaper reading.
If age is not included as a predictor in the regression model, the indirect correlation is attributed to the effect of interest in politics. The estimated effect is too strong. Once we include age as a predictor, the effect of political interest is cleansed of the age effect, so the effect size decreases.
In Figure 10.7, age is positively correlated with both political interest and newspaper reading. But a confounder that is negatively correlated with predictor and outcome has the same impact as a confounder that is positively correlated with predictor and outcome. Political cynicism, for instance, can be negatively correlated with both interest in politics and newspaper reading time (Figure 10.8). People who are less cynical about politics are more interested in politics and spend more time on reading newspapers. As a result, it looks like political interest strongly increases newspaper reading time but higher newspaper reading time is at least partly due to less political cynicism. Similar scenarios are available if the regression effect and the indirect correlation are negative.
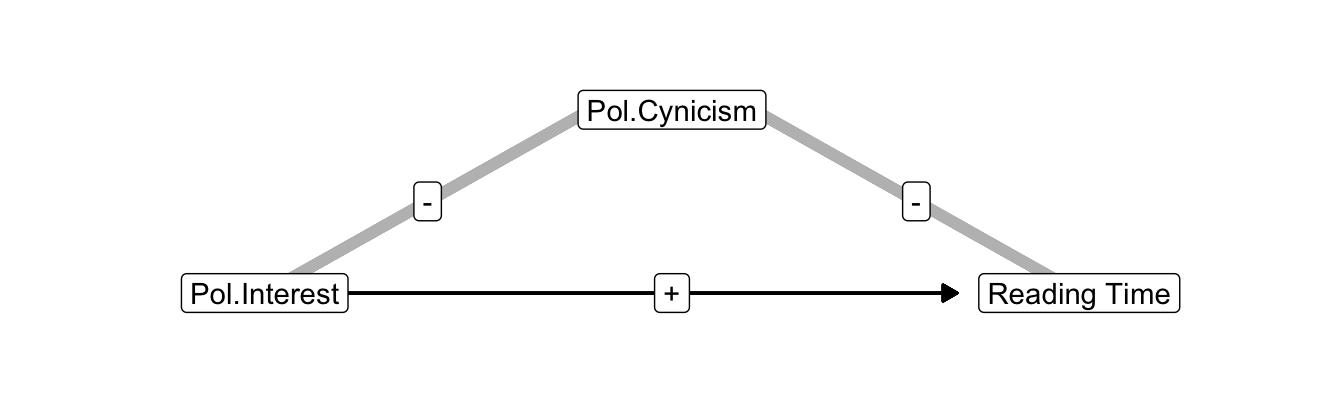
Figure 10.8: Political cynicism as a confounder of the effect of interest in politics on newspaper reading time.
As with suppression, spuriousness can have surprising results. It may happen that the entire estimated effect of a predictor is spurious. Adding a reinforcer variable to the regression model may make the entire effect of a predictor disappear. In other words, an effect that we initially thought was substantial may turn out to be too weak to be of interest.
Actually, the indirect correlation between a predictor and dependent variable due to a confounding variable can be so strong that a positive effect in a model without the confounder changes into a negative effect in a model that includes the variable. Adding the reinforcer to the model, the effect of the predictor not only moves towards zero (becoming weaker), but it moves beyond zero into a negative effect. It may even move so far beyond zero that the new negative effect is stronger than the reinforced positive effect.
The opposite may happen as well: An initially negative effect may become positive if a strong reinforcer variable is added to the model. This would be the case if the indirect correlation between political interest and newspaper reading time via news site use is strongly negative, resulting in a negative effect of political interest on reading time if news site use is left out of the model. Adding news site use to the model may then result in a positive effect of political interest.
To summarize the two types of confounders:
If we add a suppressor to the model, the suppressed effect moves away from zero because suppression disappears. A positive effect becomes more strongly positive, a negative effect becomes more strongly negative.
If we add a reinforcer to the model, the reinforced effect moves towards the opposite side because reinforcement disappears. A positive effect becomes less strongly positive or even negative and a negative effect becomes less strongly negative or even positive.