4.1 Null Hypothesis Significance Testing

Null Hypothesis Significance Testing (NHST) is the most widely used method for statistical inference in the social sciences and beyond. The logic underlying NHST is called the Neyman Pearson approach (Lehmann, 1993). Though these names are not widely known, the work of Jerzy Neyman (1894–1981) and Egon Pearson (1895–1980) still has a profound impact on the way current research is conducted, reviews are considered, and papers are published.

Our habit of formulating a null hypothesis and an alternative hypothesis for all situations not covered by the null hypothesis is generally attributed to the statistician R.A. Fisher. This, however, is not entirely correct (see, e.g., Halpin & Stam, 2006). Fisher introduced the concept of a null hypothesis (Ronald Aylmer Fisher, 1935: 18) but not the concept of an alternative hypothesis. The statisticians Jerzy Neyman and Egon Pearson introduced the idea of working with two or more hypotheses. But the two hypotheses do not cover all possible population values and they were usually not called a null and alternative hypothesis. They specify two or more different population values. A statistical test is used to determine which of the hypotheses fits the sample best. (J. Neyman & Pearson, 1933)

Egon Pearson. Photo by Grasso Luigi, Wikimedia Commons, CC BY-SA 4.0

The Neyman Pearson approach ensures tight control on the probability of making correct and incorrect decisions. It is a decision framework that gives you a clear criteria and also an indication of what the probability is that your decision is wrong. The decision in this regard, is either the acceptance or rejection of the \(H_0\) hypothesis.

The Neyman Pearson approach is about choosing your desired probability of making correct and incorrect decisions, setting up the right conditions for this, and making a decision. It considers the following:

Alpha - Determine your desired risk of drawing the wrong conclusion.
Power - Determine your desired probability of drawing the correct conclusion.
- Determine the sample size needed to achieve this.
Conduct your research with this sample size.
Determine the test statistic.
Determine if \(p\)-value \(\leq \alpha\). If so, reject \(H_0\).

The two decisions can be visualized in a \(2 \times 2\) table where in reality \(H_0\) can be true or false (\(H_A\) is true), and the decision can either be to reject \(H_0\) or not. Figure 4.1 illustrates the correct and incorrect decisions that can be made. The green squares obviously indicate that it is a good decision to reject \(H_0\) when it is infact false, and not to reject \(H_0\) if it is in reality true. And the red squares indicate that it is a wrong decision to reject \(H_0\) when it is actually true (Type I error), or not reject \(H_0\) if it is in reality false (Type II error).

Figure 4.1: NHST decision table.

Intuitively it is easy to understand that you would want the probability of an incorrect decision to be low, and the probability of a correct decision to be high. But how do we actually set these probabilities? Lets consider the amount of yellow candies from the candy factory again. In chapter 1.2 we learned that the factory produces candy bags where one fifth of the candies are supposed to be yellow. Now suppose we don’t know this and our null hypothesis would be that half or the candies would be yellow. In figure 1.4 you can set the parameter values to .5 and .2 and see what the discreet probability distributions look like.

As the candy factory produces bags with ten candies, we can look at both probability distributions. Figure 4.2 shows both distributions.

\(H_0\) Distribution
- Half of the candies in the bag are yellow
- The parameter of the candy machine is .5
- With expected value 5 out of 10

\(H_A\) Distribution
- One fifth of the candies in the bag are yellow
- The parameter of the candy machine is .2
- With expected value 2 out of 10

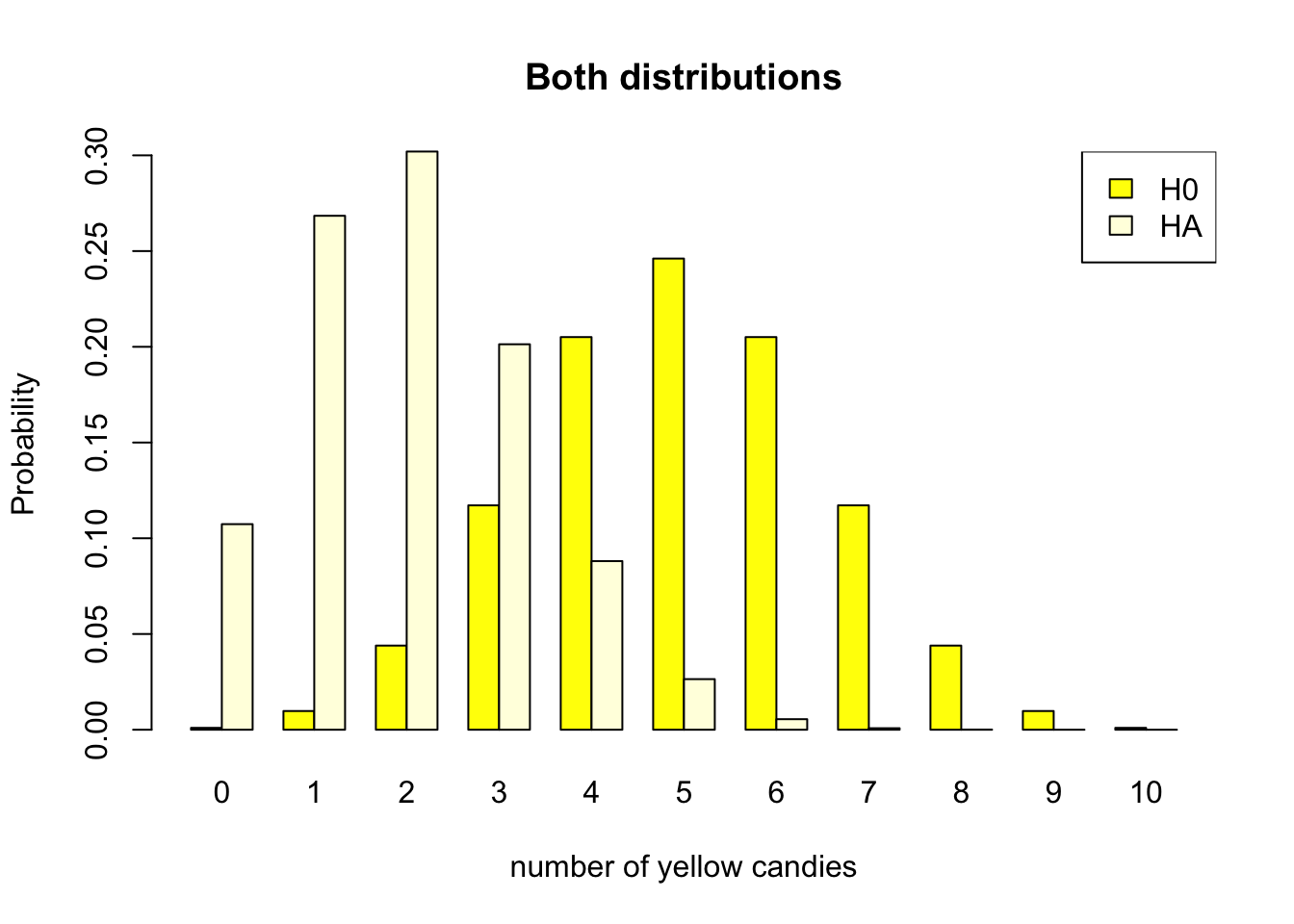
Figure 4.2: Discrete binomial distributions

We will use both distributions in figure 4.2 to clarify the different components within the Neyman Pearson approach later in this chapter. For now, take a good look at both probability distributions, and consider a bag of candy containing 4 yellow candies. Are you able to determine if this bag is the result of a manufacturing process that produces bags with 20% or 50% yellow candies.

Doing research is essentially the same. You collect one sample, and have to determine if the effect of your study is non existent (\(H_0 = \text{true}\)) or that there is something going on (\(H_0 \neq \text{true}\)).

Statistical hypotheses come in pairs: a null hypothesis (H₀) and an alternative hypothesis (H₁ / H_A). We met the null hypothesis in the preceding sections. We use it to create a (hypothetical) sampling distribution. To this end, a null hypothesis must specify one value for the population statistic that we are interested in, for example, .5 or .2 as the proportion of yellow candies.

4.1.1 Null hypothesis

The null hypothesis reflects the skeptical stance in research. It assumes that there is nothing going on. There is no difference between experimental condition, there is no correlation between variables, there is no predictive value to your regression model, a coin is fair, and so forth. Though a null hypothesis can be expressed as a single value, that does not mean that we always get that specific value when we take a random sample.

If our null assumption of our candy factory machine is that it produces bags with 5 out of 10 yellow candies, then there is still a chance that some bags will contain just one yellow candy of even 0 yellow candies. As can be seen in figure 4.3.

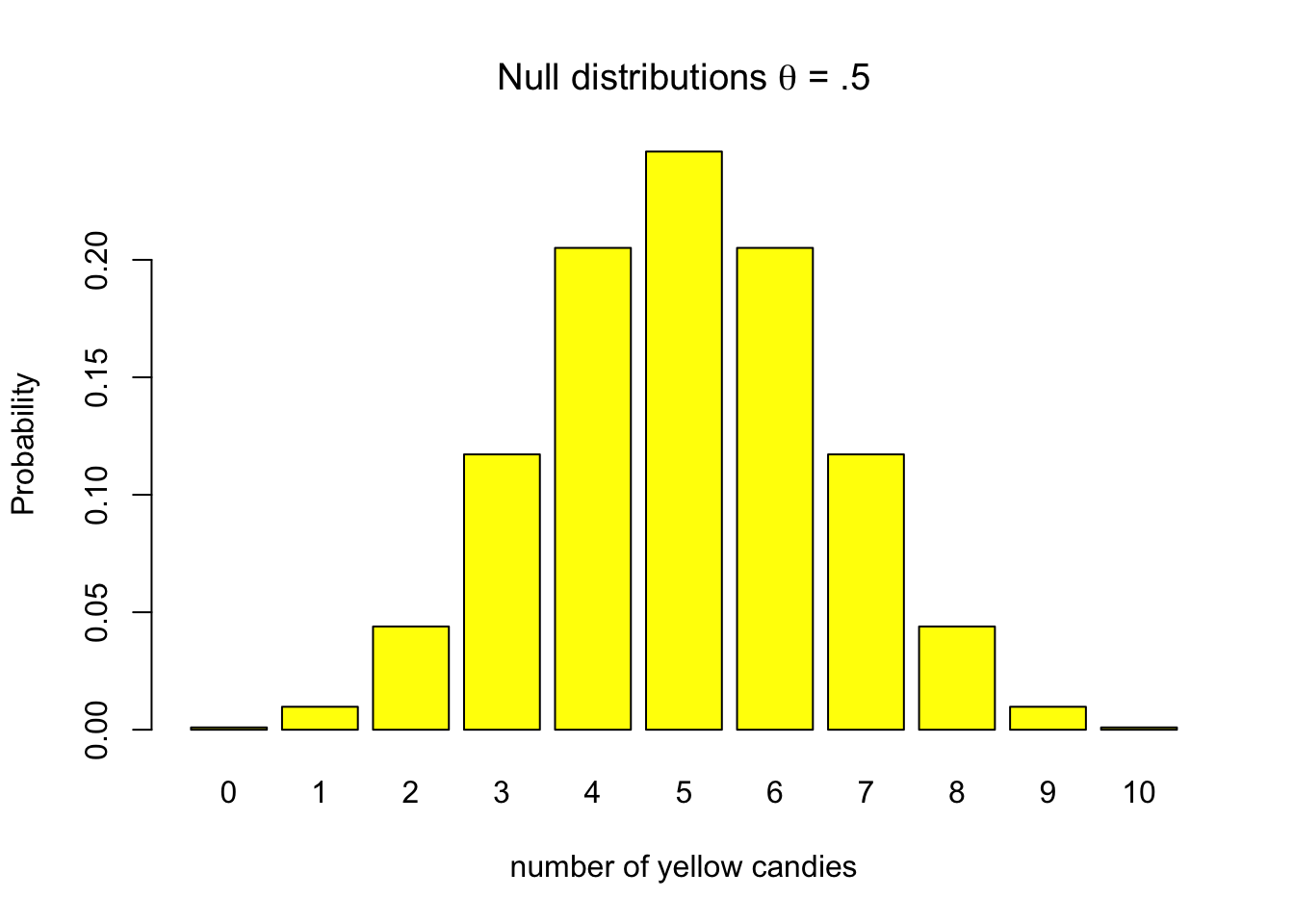
Figure 4.3: Discrete binomial distributions

4.1.2 Alternative hypotesis

The assumption that a researcher wants to test is called a research hypothesis. It is a statement about the empirical world that can be tested against data. Communication scientists, for instance, may hypothesize that:

a television station reaches half of all households in a country,
media literacy is below a particular standard (for instance, 5.5 on a 10-point scale) among children,
opinions about immigrants are not equally polarized among young and old voters,
the celebrity endorsing a fundraising campaign makes a difference to adult’s willingness to donate,
more exposure to brand advertisements increases brand awareness among consumers,
and so on.

These are statements about populations: all households in a country, children, voters, adults, and consumers. As these examples illustrate, research hypotheses seldom refer to statistics such as means, proportions, variances, or correlations. Still, we need a statistic to test a hypothesis. The researcher must translate the research hypothesis into a new hypothesis that refers to a statistic in the population, for example, the population mean. The alternative hypothesis therefore indicates what the researcher expects in terms of effects, differences, deviation from null. It is the operationalisation of what you expect to find if your theory would be accurate.

In case of our candy factory example, the alternative hypothesis would be that the machine produces bags with 2 out of 10 yellow candies and that the machines parameter is .2, one in five yellow candies per bag. Assuming this parameter, does not ensure that every bag will contain exactly 2 yellow candies. Some bags will contain 0, 1, 3, 4, 5, 6, 7, 8, 9, or even 10 yellow candies. The probabilities for each can again be visualized using the exact discrete binomial probability distribution (figure 4.4) as we did for the null hypothesis.

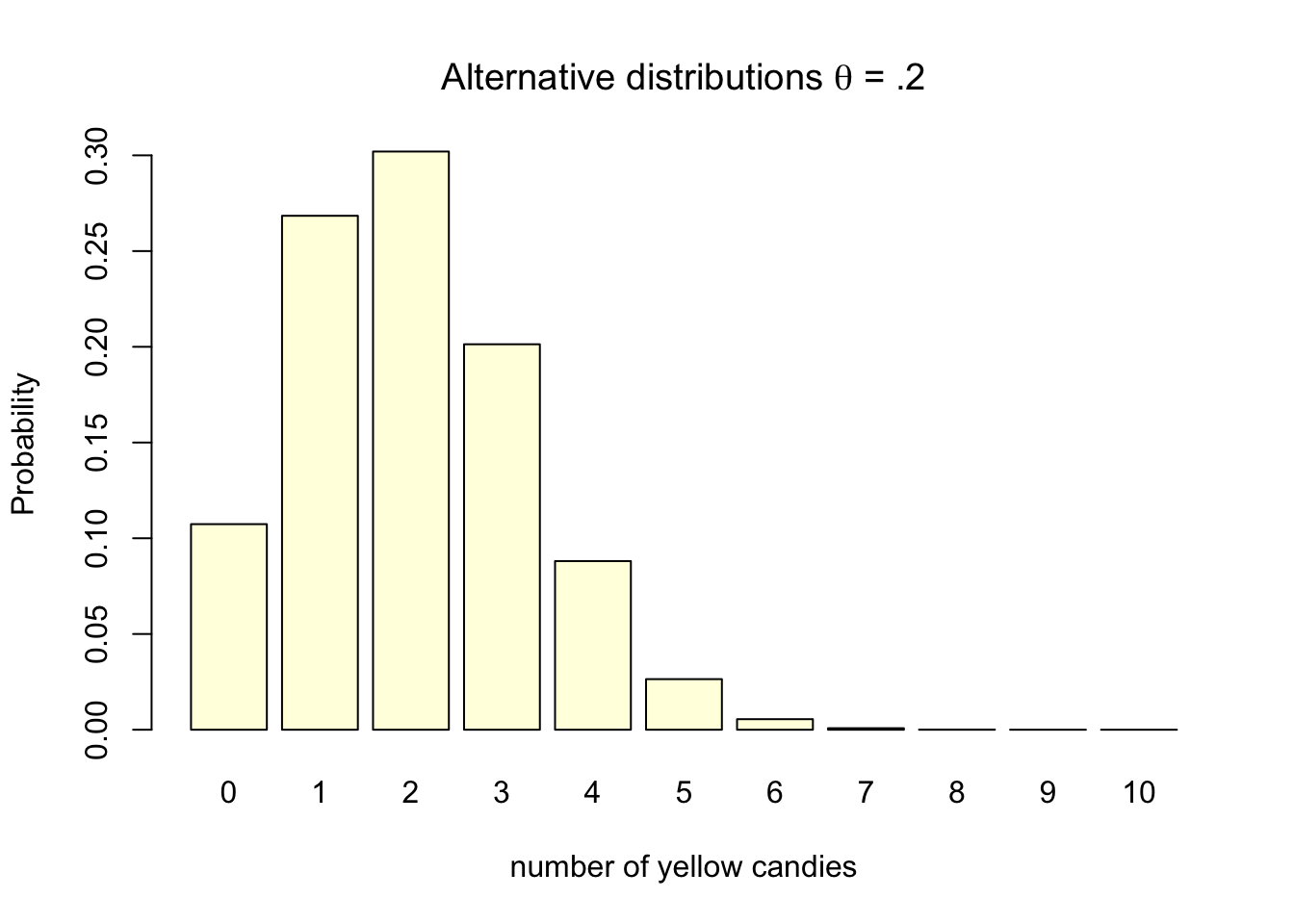
Figure 4.4: Discrete binomial distributions

Note that both the probability distribution for \(H_0\) and for \(H_A\) contain the results of assumptions about reality, and that at this stage only the sample size, the amount of candies in a bag (10) has been used to determine the distribution. No data has been gathered yet in determining these distributions. It is all based on assumptions.

4.1.3 True effect size

The true effect size is the difference between the null hypothesis and the true alternative hypothesis. In the candy factory example, the true effect size is .5 - .2 = .3. This is the difference in the proportion of yellow candies in the bags. In figure 4.5 you can see the difference in the two distributions. The true effect size is the difference in the expected value of the two distributions. In absolute terms, it it the 5 - 3, though, in terms of the parameter it is the proportion .5 - .2.

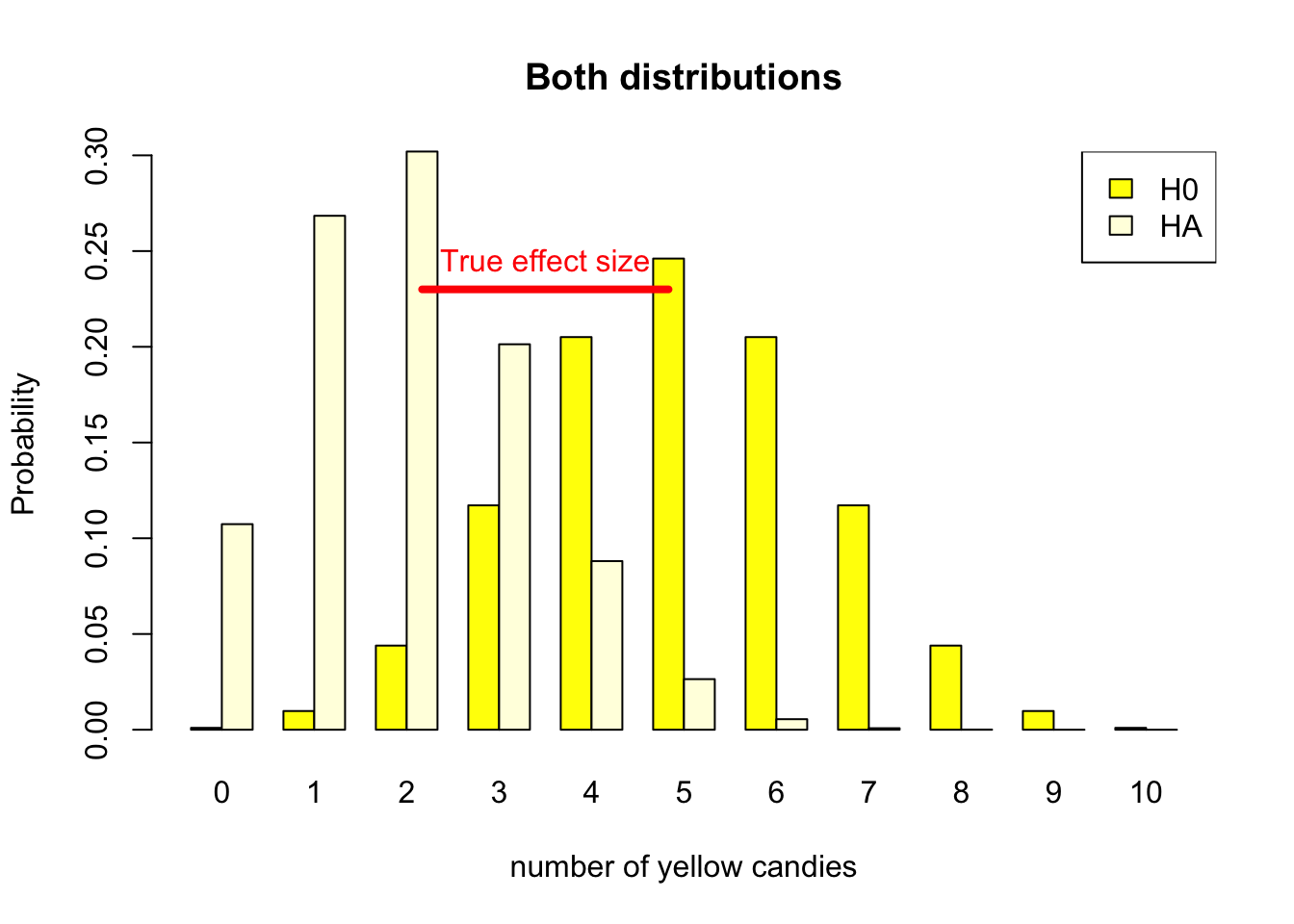
Figure 4.5: Discrete binomial distributions

True refers to the actual difference in the population. The problem is that we do not know this difference. In our candy factory example, we can only observe the specific candy bag. Have an assumption about the null hypothesis and the alternative hypothesis. Though the true effect size refers only to the actual effect in the population, the actual difference, the actual correlation, the actual parameter value.

Understanding the null and alternative hypothesis and their associated probability distributions is crucial for grasping the logic of the Neyman Pearson approach. In the following chapters, we will use these distributions to explain the different components of the Neyman Pearson approach.

4.1.4 Alpha

The first step in the Neyman Pearson approach is to set the desired Type I error rate, also known as the significance level, \(\alpha\). This is the probability of rejecting the null hypothesis when it is in reality true. In the \(2 \times 2\) descision table in figure 4.6, this corresponds to the top left quadrant.

As a researcher, you decide how much risk you are willing to take to make a Type I error. As the Neyman Pearson approach is a decision framework, you have to set this probability before you start collecting data. The most common value for \(\alpha\) is .05, which means that you accept a 5% chance of making a Type I error.

Figure 4.6: NHST decision table.

In our yellow candy example, assuming the null hypothesis to be true, relates to the parameter value of .5 and the associated probability distribution shown in figure 4.3. We have already determined that if \(H_0\) is true, it is still possible we could get a bag with 0 or 10 yellow candies. Deciding to reject the null hypothesis in any of these cases, would be wrong, because the null hypothesis is assumed to be true. The exact probabilities can be found on the y-axis of figure 4.3, and are also shown in the table 4.1 below. Looking at the probability of getting 0 or 10 candies in table 4.1, we see that together this amounts to .002 or 0.2%. If we would decide to only reject the null hypothesis if we would get 0 or 10 candies, this would be a wrong decision, but we would also know that the chance of such a decision is pretty low. Our Type I error, alpha, significance level, would be .002.

Table 4.1: Probabilities of drawing a certain amount of yellow candies from a bag of 10 candies, assuming the null hypothesis to be true.
Yellow	0	1	2	3	4	5	6	7	8	9	10
Prob	0.001	0.010	0.044	0.117	0.205	0.246	0.205	0.117	0.044	0.010	0.001

Choosing such an alpha level would result in a threshold between 0 and 2 and 9 and 10. We call this the critical value associated with the chosen alpha level. Where on the outside of the threshold we would reject the null hypothesis, and inside the threshold we would not reject the null hypothesis. So, if that is our decision criteria, we would reject the null hypothesis if we would draw a bag with 0 or 10 yellow candies, and not reject the null hypothesis if we would draw a bag with 1, 2, 3, 4, 5, 6, 7, 8, or 9 yellow candies. Amounting to a Type I error rate of .002 or 0.2%. Figure 4.7 shows the critical values for the null hypothesis distribution, and indicate what de decision would be for values on the outside and inside of the decision boundary.

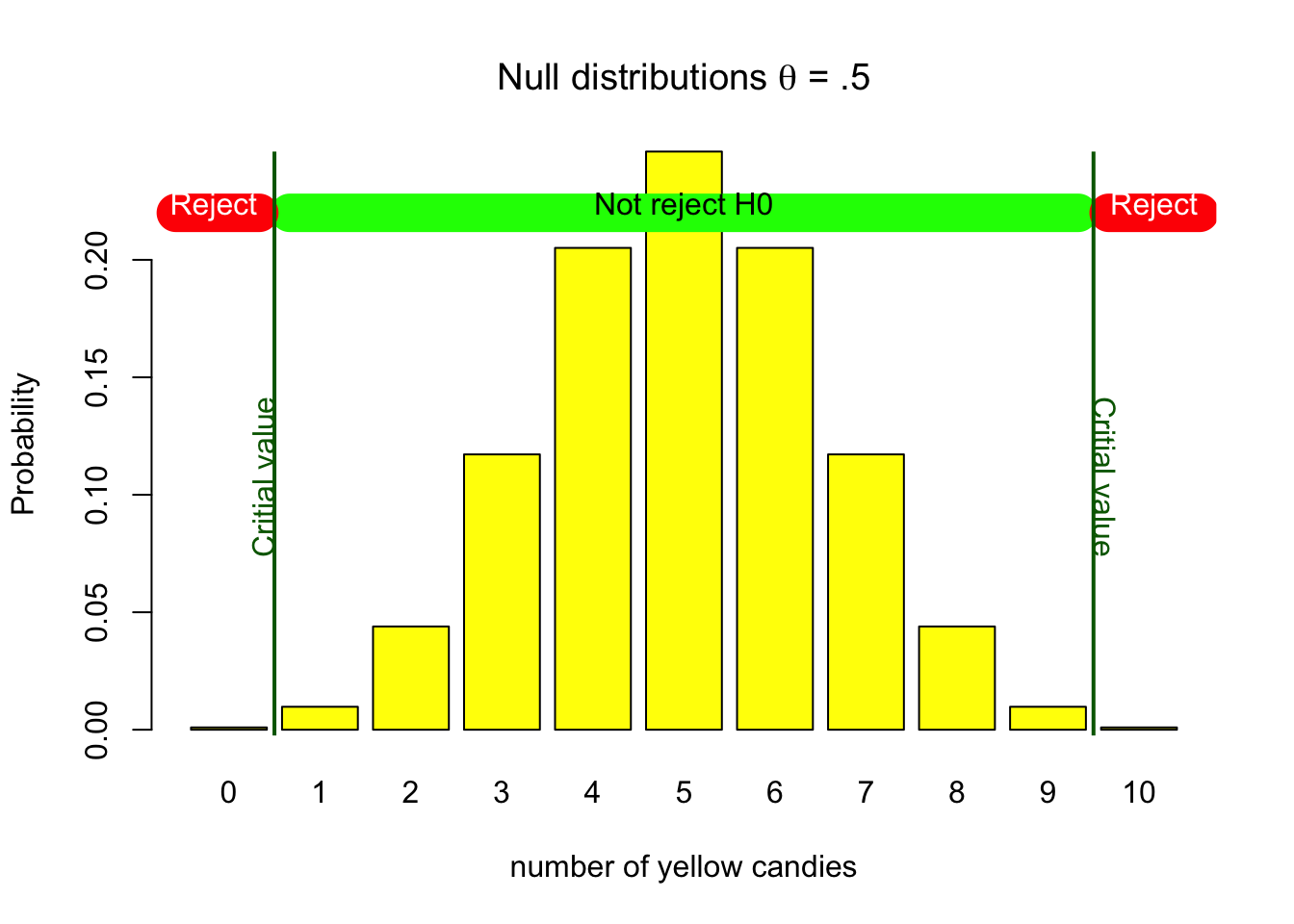
Figure 4.7: H0 binomial distributions with critical values

In the social sciences, we allow ourselves to make a wrong descision more often. We usually set the alpha level to .05. For our discreet example setting the alpha level to .05 is not really possible. Looking at table 4.1, we could raise the significance level to .044 if we would reject the null hypothesis if we would draw 0, 1, 2,, 8, 9 or 10 yellow candies. This would result in a Type I error rate of 4.4%. Though if we would also reject the null hypothesis with 3 or 7 yellow candies, we would have a Type I error rate of 5.7%. For a discrete probability distribution with a limited number of outcomes, it is not always possible to set the alpha level exactly to .05.

For continuous probability distributions, such as the normal distribution, it is possible to set the alpha level exactly to .05. For example the null hypothesis that average media literacy in the population of children equals 5.5 on a scale from one to ten.

We can construct a sampling distribution around the hypothesized population value. Remember (Section 1.2.4) that the population value is the expected value of the sampling distribution, that is, its mean (if the estimator is unbiased). The sampling distribution, then, is centered around the population value specified in the null hypothesis. This sampling distribution tells us the probabilities of all possible sample outcomes if the null hypothesis is true. It allows us to identify the most unlikely samples. In step two in figure 4.8, we set the alpha level to .05. This means that we cut off 2.5% of the area in each tail of the sampling distribution. The critical values are the values that separate the 2.5% of the area in each tail from the 95% of the area in the middle. If we assume the population parameter to be 5.5, rejecting the null hypothesis would again be a wrong decision. Thus setting the boundary by using an alpha level of .05, would yield a wrong decision in 5% of the samples we take. Just like the discrete candy color case, we decide to reject \(H_0\) on the outside of the critical value and not reject \(H_0\) on the inside of the critical value.

Figure 4.8: Sampling distribution of average media literacy according to the null hypothesis.

Note that the reasoning for the discrete case and the continuous case is the same. The only difference is that for the continuous case we can set the alpha level exactly to .05.

4.1.5 1 - Alpha

The decision to not reject the null hypothesis when it is in reality true is indicated by \(1 - \alpha\). It does not go by any other name, but in terms of probability, it is directly dependent on your desired type I error rate, your chosen alpha level. It therefore corresponds to probability of 1, 2, 3, 4, 5, 6, 7, 8, or 9 yellow candies in the candy factory example, a 99.8% (1 - .002) chance of making the correct decision. The inside of the critical value in figure 4.7 is the area where we do not reject the null hypothesis. In the \(2 \times 2\) decision table in figure 4.1, this corresponds to the bottom left green quadrant.

Now that we have determined our critical value based on our desired alpha, significance level, we can use this to look at the power.

4.1.6 Power

The power refers to the probability of making the correct decision when the null hypothesis is false. In the \(2 \times 2\) decision table in figure 4.1, this corresponds to the top right quadrant. As we have already set our decision criteria by choosing our alpha level in the previous step, we already know when we decide to reject the null. In figure (fig:nulldistributionalpha) we determined our type I error could be 0.2%, if we would reject the null hypothesis if we would draw 0 or 10 yellow candies. The critical value would in that case be between 0 and 1 and 9 and 10. This critical value carries over when determining the power.

Though, as we assume the null hypothesis to be false, we need to specify what alternative distribution to use. We already established that this would be the distribution with a parameter value of .2. In figure 4.9, we see that our descision criteria is still the same. That we decide to reject the null when we sample 0 or 10 yellow candies. But the distribution has now changed.

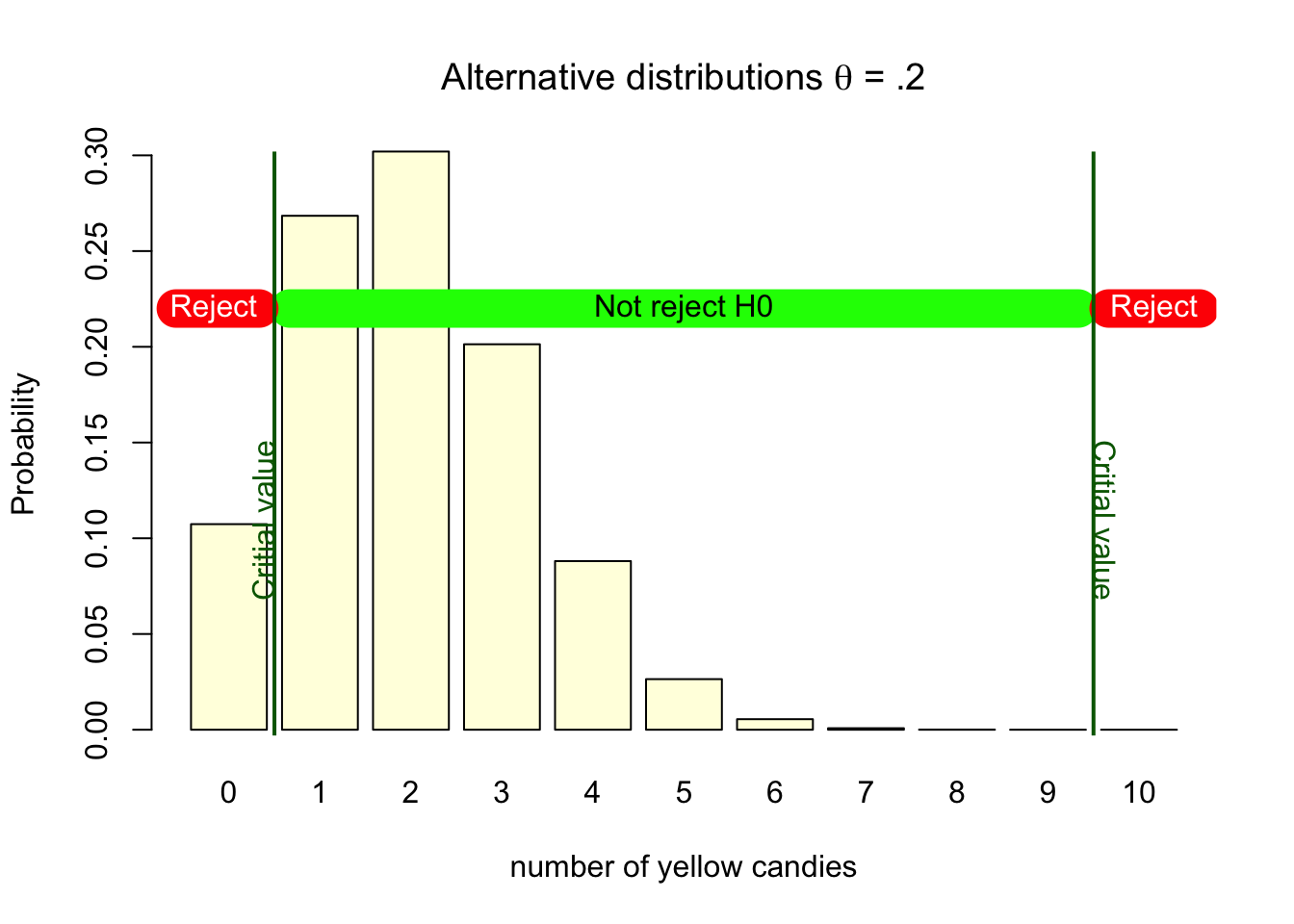
Figure 4.9: H0 binomial distributions with critical values

If this alternative distribution would actually be true, deciding to reject the null would be a good decision. Though, we can also see that if this alternative is true, if the parameter turly is .2, getting a bag with 0 or 10 yellow candies does not happen that often. The probabilities for 10 yellow candies is almost none, and the probability for getting 0 yellow candies is about 11%. This means that if the alternative hypothesis is true, if our sample originates from the alternative hypothesis, we would only make the decision to reject the null hypothesis in 11% of the samples we get out of it. So, the power of the test, correctly rejecting the null when this specific alternative is true is only 11%.

The only way to increase the power is to increase the sample size of the study.

As stated earlier we would rather have a high probability of making the correct decision. In the social sciences we are striving for a power of .80. This means that we want to make the correct decision in 80% of the cases when the null hypothesis is false. In our candy factory example, this would mean that we would want to reject the null hypothesis in 80% of the replications. With our machine producing bags with 10 candies, this is just not possible. The only way to increase the power is to increase the sample size of the study. In the candy factory example, this would mean that we would have to increase the number of candies in the candy bags. We will come back to this in the chapter 3.3.1 on sample size.

One more thing to note, is that the true power of the test is only known when the alternative hypothesis is true. In practice, we do not know if the null or the alternative hypothesis is true. We can only calculate the power of the test when we assume some alternative hypothesis. It is good practice to base your assumptions about the alternative hypothesis on previous research, theory, or other empirical evidence. This is mostly expressed as the expected effect size, the expected difference between the null and the alternative hypothesis.

In all statistical software, the power of the test is not calculated based on the true effect size, but on the found effect size in your sample. This is called the observed power and will be covered in chapter 4.1.10.

4.1.7 Beta

The probability of making a Type II error is indicated by \(\beta\). It is the probability of not rejecting the null hypothesis when it is in reality false. In the \(2 \times 2\) decision table in figure 4.1, this corresponds to the bottom right quadrant. The power of the test is \(1 - \beta\). In our candy factory example, the power of the test is .11, so the probability of making a Type II error is .89. It is the probability of getting a bag with 1, 2, 3, 4, 5, 6, 7, 8, or 9 yellow candies, when the machine actually produces bags with 2 yellow candies, the addition of the height of the bars in figure 4.9 for these values.

4.1.8 Test statistic

In chapter 1.2.1 we discussed the sample statistic, and defined it as any value describing a characteristic of the sample. This could be the mean, or the proportion, or the correlation, or the regression coefficient. It is a value that is calculated from the sample. Note that also conversions of the sample statistic, such as the difference between two sample means, or the ratio of two sample variances, \(t\)-values, \(F\)-values, and \(\chi^2\)-values are also sample statistics.

The test statistic is a sample statistic that is used to test the null hypothesis. In our candy factory example, the test statistic would be the number of yellow candies in the bag we sample. If we would draw a bag with 4 yellow candies, the test statistic would be 4.

In the previous sections, we have determined our decision criteria, the critical value, based on our desired alpha level. We have also determined the power of the test, based on the alternative hypothesis. The test statistic is used to determine if we reject the null hypothesis or not. If the test statistic is outside the critical value, we reject the null hypothesis. If the test statistic is inside the critical value, we do not reject the null hypothesis.

Looking at figure 4.7, we see that the critical value is between 0 and 1 and 9 and 10. If we would draw a bag with 4 yellow candies, we can check if the value 4 is inside or outside the critical value. As 4 is inside the critical value, we would not reject the null hypothesis.

The test statistic is the value that is used to decide if we reject the null hypothesis or not.

In the continuous case, as described in figure 4.8, the test statistic is the sample mean. If the sample mean is outside the critical value, we reject the null hypothesis. If the sample mean is inside the critical value, we do not reject the null hypothesis. If you select Step 4 in figure 4.8, and draw a few samples, you can see if the test statistic, the sample mean, is inside or outside the critical value. Again, the reasoning for the continuous case is the same as for the discrete case.

4.1.9 P-value

How do we know that the test statistic that we have drawn is among the five percent most unlikely samples if the null hypothesis is true? In other words, how do we know that our sample statistic outcome is in the rejection region?

The p-value is the probability of obtaining a test statistic at least as extreme as the result actually observed, under the assumption that the null hypothesis is true.

We have learned that a test is statistically significant if the test statistic is in the rejection region. Statistical software, however, usually does not report the rejection region for the sample statistic. Instead, it reports the p value of the test, which is sometimes referred to as significance or Sig. in SPSS.

In the previous section we considered a sample with 4 yellow candies. The p-value considers the probability of such a sample, but also ads the probability of getting a sample with less yellow candies. This is what is meant with “at least as extreme”. this is not really intuitive, but it refers to the less likely test statistics, in our case 0, 1, 2 and 3, are even less probable than 4. The assumption that the null hypothesis is true indicates that we need to look at the probabilities from the null distribution. Looking at table 4.1, we see that the probability of getting 0, 1, 2, 3 or 4 yellow candies under the null distribution is 0.001 + 0.010 + 0.044 + 0.117 + 0.205 = 0.377. This is the p-value. The conditional probability of getting a sample that is as or less likely than the test statistic that we have. The conditional probability is referring to our assumption that the null hypothesis is true.

The reasoning applied when comparing our test statistic to the critical value is the same as when comparing the p-value to the alpha level. If the p-value is smaller or equal to than the alpha level, we reject the null hypothesis. If the p-value is larger than the alpha level, we do not reject the null hypothesis.

If the test statistic is within the critical values, the p-value is always larger than the alpha level. If the test statistic lies outside the critical value, the p-value is always smaller than the alpha level. In the case that the test statistic is exactly the same as the critical value, the p-value is exactly equal to the alpha level, we still decide to reject the null hypothesis.

Reject \(H_0\) when \(p\)-value \(\leq \alpha\)

As both the p-value and the alpha level assume the null to be true, you can find both probabilities under the null distribution. In the continuous case, the p-value is the area under the curve of the probability distribution that is more extreme than the sample mean. The significance level is chosen by you as a researcher and is fixed.

It is important to remember that a p value is a probability under the assumption that the null hypothesis is true. Therefore, it is a conditional probability.

Compare it to the probability that we throw sixes with a dice. This probability is one out of six under the assumption that the dice is fair. Probabilities rest on assumptions. If the assumptions are violated, we cannot calculate probabilities.

If the dice is not fair, we don’t know the probability of throwing sixes. In the same way, we have no clue whatsoever of the probability of drawing a sample like the one we have if the null hypothesis is not true in the population.

Figure 4.10 shows a t-distribution for a null assumption with an alpha level of 5% (red area) and the p-value (blue area) for a random sample with a t-value of 2. For a two sided test (left) and a one sided test (right). We will cover one and two sided testing in chapter 4.1.14.

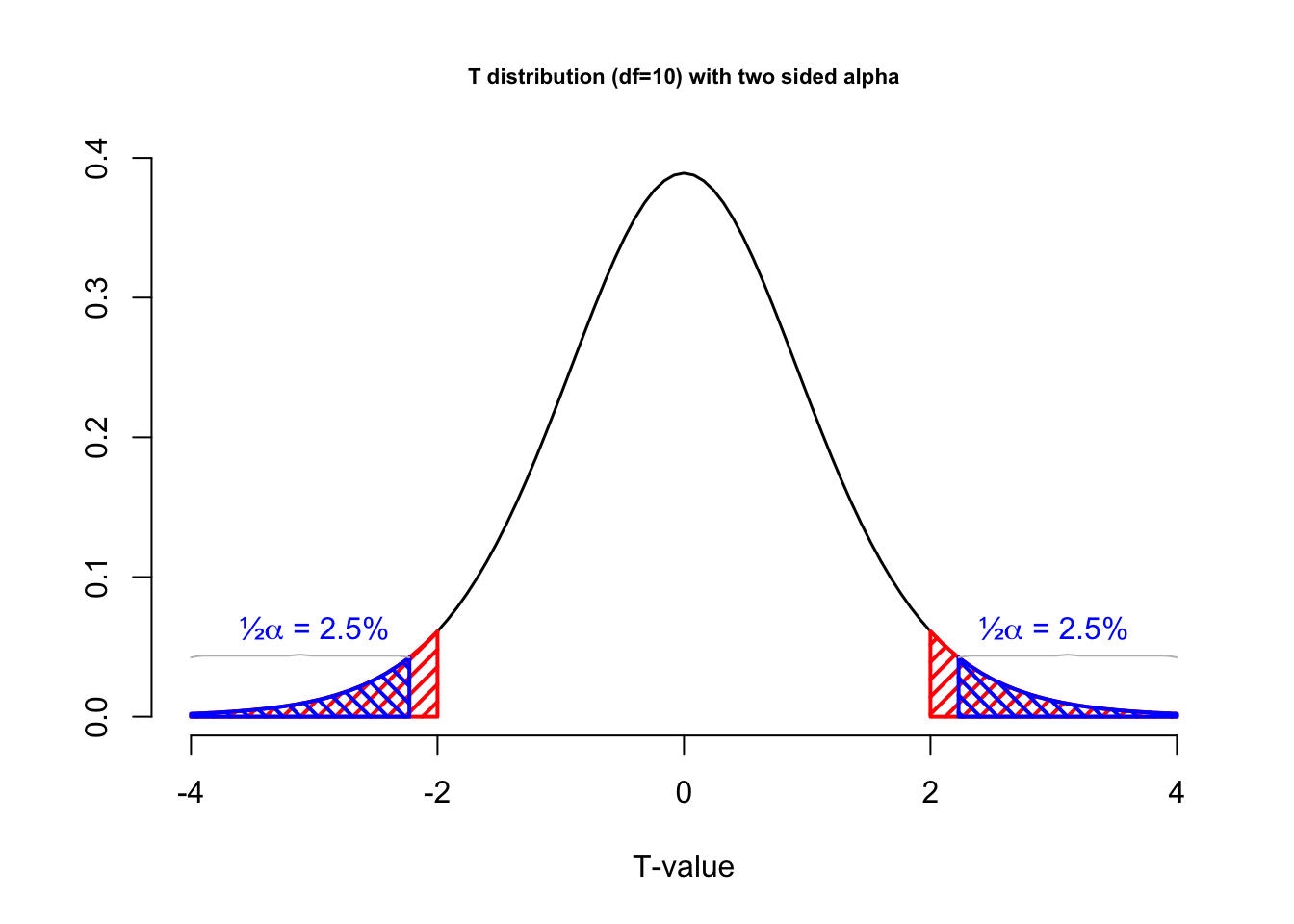
Figure 4.10: T-distributions with alpha level and p-value

In figure 4.10, the red vertical boundaries represent the critical value associated with a chosen alpha level of 5%, the red area under the curve. The blue vertical line represents the t-value from the sample, which in this example was 2. The blue area under the curve represents the p-value, the probability of getting this t-value or more extreme.

Figure 4.11 representing the sampling distribution of average media literacy. You can take a sample and play around with the population mean according to some null hypothesis. If the mean in the sample is outside the critical value, it falls in the alpha rejection region.

Figure 4.11: Sampling distribution of average media literacy according to the null hypothesis.

The reasoning is again the same as in the discrete case. If the p-value is smaller or equal to the alpha level, we reject the null hypothesis. If the p-value is larger than the alpha level, we do not reject the null hypothesis.

4.1.10 Observed effect size

In chapter 4.1.3 we discussed the true effect, the difference between the null hypothesis and the alternative hypothesis. The problem is that we do not know the true effect, we do not know wich of the two hypothesis is actually true. In some cases we don’t even know if our expected alternative hypothesis is correct.

We can only estimate the true effect using the sample statistic. The difference between the sample statistic and the null hypothesis is called the observed effect size. In the candy factory example, the observed effect size is the difference between the number of yellow candies in the sample and the number of yellow candies in the null hypothesis. If the null hypothesis is that the machine produces bags with 5 yellow candies, and the sample contains 4 yellow candies, the observed effect size is 1.

The same defenition holds for the continuous case. If the null hypothesis is that the average media literacy in the population is 5.5, and the sample mean is 3.9, the observed effect size is 1.6. Or if we hypothesize that average candy weight in the population is 2.8 grams and we find an average candy weight in our sample bag of 2.75 grams, the effect size is -0.05 grams. If a difference of 0.05 grams is a great deal to us, the effect is practically relevant.

Note that the effect sizes depend on the scale on which we measure the sample outcome. The unstandardized effect size of average candy weight changes if we measure candy weight in grams, micro grams, kilograms, or ounces. Of course, changing the scale does not affect the meaning of the effect size but the number that we are looking at is very different: 0.05 grams, 50 milligrams, 0.00005 kilos, or 0.00176 ounces. For this reason, we do not have rules of thumb for interpreting these unstandardized effect sizes in terms of small, medium, or large effects. But we do have rules of thumb for standardized effect sizes.

You can imagine that estimating the true effect size on just one sample is not very reliable. The observed effect size could be the result of our sample being the result of the null being true, or the alternative being true. The way researchers try to get a notion of the true effect size is by replicating the study. If the observed effect size is consistent over multiple replications, we can be more confident that the average observed effect size is the true effect size. This is what we will cover in chapter 4.1.12 about meta analysis.

4.1.10.1 Standardized effect size: Cohen’s d for one or two means

In scientific research, we rarely have precise norms for raw differences (unstandardized effects) that are practically relevant or substantial. For example, what would be a practically relevant attitude change among people exposed to a health campaign?

To avoid answering this difficult question, we can take the variation in scores (standard deviation) into account. In the context of the candies example, we will not be impressed by a small difference between observed and expected (hypothesized) average candy weight if candy weights vary a lot. In contrast, if candy weight is quite constant, a small average difference can be important.

For this reason, standardized effect sizes for sample means divide the difference between the sample mean and the hypothesized population mean by the standard deviation in the sample. Thus, we take into account the variation in scores. This standardized observed effect size for tests on one or two means is known as Cohen’s d.

These are the formulas for Cohen’s d for a one-sample t test, a paired-samples t test, and an independent-samples t test (they will be provided if needed):

\[\begin{equation} d_{one_-sample} = \frac{M - \mu_0}{SD} \end{equation}\] \[\begin{equation} d_{paired_-samples} = \frac{M_{diff} - \mu_{0_-diff}}{SD_{diff}} \end{equation}\] \[\begin{equation} d_{independent_-samples} = \frac{2*t}{\sqrt(df)} \end{equation}\]

Where:

\(M\) is the sample mean, \(\mu_0\) is the hypothesized population mean, and \(SD\) is the standard deviation in the sample,
\(M_{diff}\) is the difference between the two means in the sample, \(\mu_{0_-diff}\) is the hypothesized difference between the two means in the population mean, which is zero in case of a nil hypothesis, and \(SD_{diff}\) is the standard deviation of the difference in the sample,
\(t\) is the test statistic value and \(df\) is the number of degrees of freedom of the t test.

The sample outcome can be a single mean, for instance the average weight of candies, but it can also be the difference between two means, for example, the difference in colourfulness of yellow candies at the beginning and end of a time period. In the latter case, the standard deviation that we need is the standard deviation of colourfulness difference across all candies (Section 2.3.6). In the case of independent samples, such as average weight of red versus yellow candies, we need a special combined (pooled) standard deviation for yellow and red candy weight that is not reported by SPSS. Here, we use the t value and degrees of freedom to calculate Cohen’s d.

Using an inventory of published results of tests on one or two means, Cohen (1969) proposed rules of thumb for standardized effect sizes (ignore a negative sign if it occurs):

0.2: weak (small) effect,
0.5: moderate (medium) effect,
0.8: strong (large) effect.

Note that Cohen’s d can take values above one. These are not errors, they reflect very strong or huge effects (Sawilowsky, 2009).

4.1.10.1.1 Obtaining Cohen’s d with SPSS

Figure 4.12: Obtaining Cohen’s d with SPSS.

Unfortunately, the t test commands in SPSS have no option to calculate Cohen’s d. It is, however, relatively easy to calculate Cohen’s d by hand from SPSS output. Remember that we must divide the unstandardized effect by the standard deviation.

For a t test on one mean, the unstandardized effect is the difference between the sample mean and the hypothesized mean. SPSS reports this value in the column Mean Difference of the table with test results. Drop any negative signs! Divide it by the standard deviation of the variable as given in Table One-Sample Statistics.

In the example, Cohen’s d is 0.036 / 0.169 = 0.21. This is a weak effect.

For a paired-samples t test, the unstandardized effect size is reported in the column Mean in the Table Paired Samples Test. The standard deviation of the difference can be found in column Std. Deviation in the same table. Divide the first by the second, for instance, 1.880 / 1.033 = 1.82. This is a strong effect.

For an independent-samples t test, the situation is less fortuitous because SPSS does not report the pooled sample standard deviation that we need. The pooled sample standard deviation takes a sort of average of the outcome variable’s standard deviations in the two groups. As an approximation, we can calculate Cohen’s d as follows: Double the t value and divide it by the square root of the degrees of freedom.

In the example, Cohen’s d equals \((2 * 0.651) / \surd(18) = 0.31\). This is a moderate effect size.

4.1.10.2 Association as effect size

Measures of association such as Pearson’s product-moment correlation coefficient or Spearman’s rank correlation coefficient express effect size if the null hypothesis expects no correlation in the population. If zero correlation is expected, a correlation coefficient calculated for the sample expresses the difference between what is observed (sample correlation) and what is expected (zero correlation in the population).

Effect size is also zero according to the standard null hypotheses used for tests on the regression coefficient (b), R² for the regression model, and eta² for analysis of variance. As a result, we can use the standardized regression coefficient (Beta in SPSS and b* according to APA), R², and eta² as standardized effect sizes.

Because they are standardized, we can interpret their effect sizes using rules of thumb. The rule of thumb for interpreting a standardized regression coefficient (b*) or a correlation coefficient, for example, could be that a value between 0 and .10 is interpreted as no or a very weak association, between .10 and .30 as weak, between .30 and .50 as moderate, .50 to .80 as strong, and .80 to 1.00 as very strong, while exactly 1.00 is a perfect association. Note that we ignore the sign (plus or minus) of the effect when we interpret its size.

4.1.11 Post hoc power

Just as the observed effect size is based on the test statistic acquired from your sample, so is the post hoc power. It is also known as: observed, retrospective, achieved, prospective and a priori power (O’Keefe, 2007).

The power of a test assuming a population effect size equal to the observed effect size in the current sample.

The post hoc power refers to the probability of rejecting the null hypothesis assuming the alternative hypothesis has a population mean equal to the observed sample mean or more accurately the observed test statistic. Though SPSS produces this when you ask it, it is obvious that multiple replications of a research study will yield different results. As the true population mean is not a random variable, the actual power is fixed and should not vary.

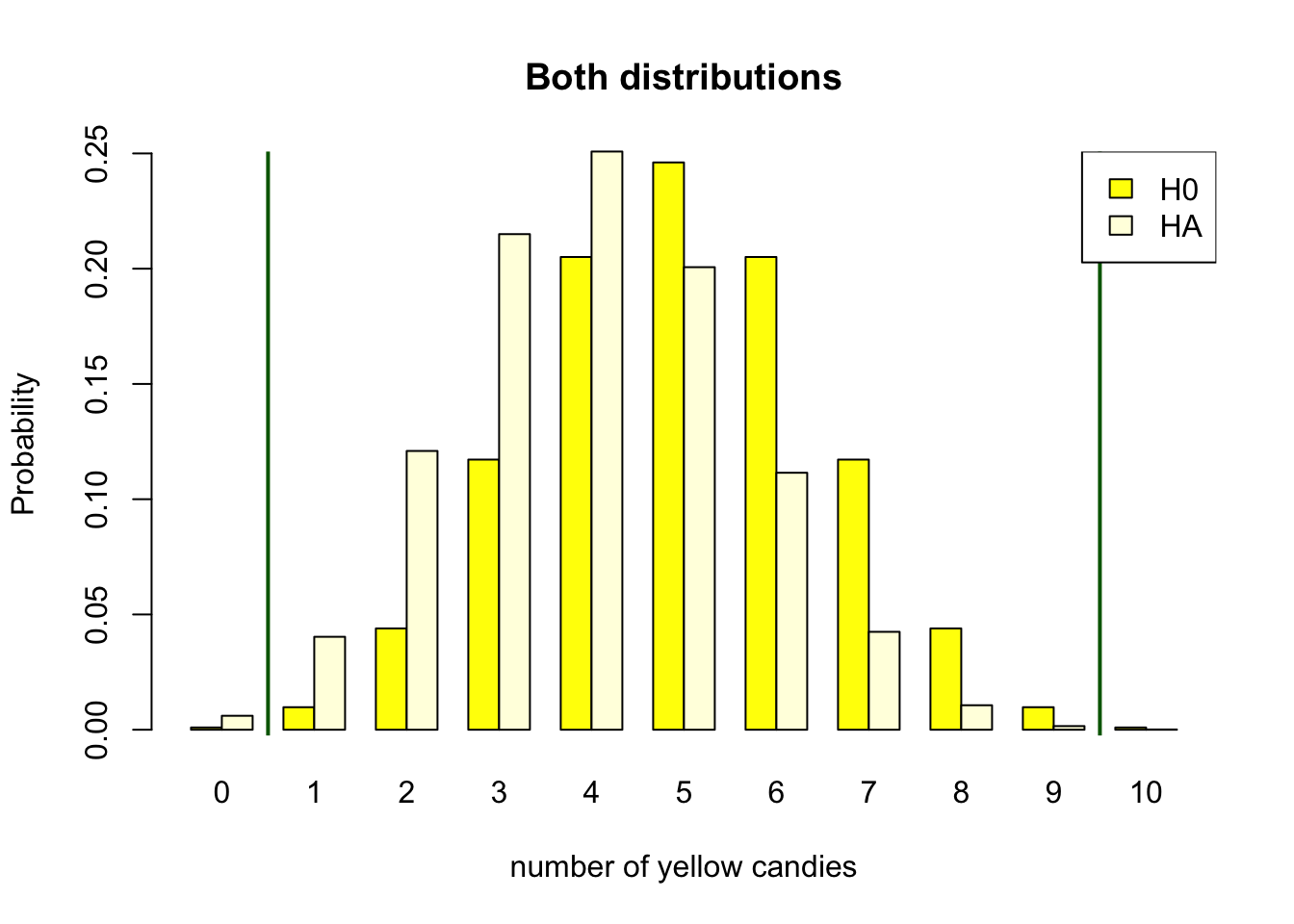
Figure 4.13: Discrete binomial distributions showing post hoc power

Figure 4.13 shows the post hoc power for a sample of 10 candies. The null hypothesis is that the machine produces bags with 5 yellow candies. The alternative hypothesis is that the machine produces bags with 2 yellow candies. But the post hoc power assumes the found test statistic of 4 candies to be the alternative population parameter of .4. Following the same decision criteria as defined in the previous sections, the post hoc power is almost zero. This is the probability of 0 or 1 yellow candies under the alternative distribution.

You can imagine that if we look at a different candy bag and we would find 7 yellow candies, the post hoc power would be not be the same higher. The post hoc power does not have much practical use, though you should be warned that this is what SPSS produces when you ask for power.

4.1.12 Meta analysis

As mentioned in chapter 4.1.10, the observed effect size is based on the sample statistic, and will differ with every sample you take. If our research hypothesis is actually true, than a random sample from the alternative distribution would more often result in sampled number of yellow candies close to 2. But as we have seen in figure 4.4, getting 4 yellow candies is reasonably probable.

Now imagine that we would take multiple samples from the alternative distribution, and calculate the observed effect size for each sample. If we would plot these observed effect sizes, we would get a sampling distribution of observed effect sizes.

In research we conduct replication studies to see if the observed effect size is consistent over multiple replications. If this is the case, we can be more confident that the average observed effect size is the true effect size and we can determine the parameter of the alternative hypothesis.

Again imagine that we get a hundred bags of candy and we consistently find 7 to 9 yellow candies, this would give us an indication of the true effect size being 8. It would also indicate that our initial alternative hypothesis is highly unlikely. This is essentially what meta analysis is about. Collecting effect sizes from multiple studies and combining them to get an indication of the true effect size.

[to-do] add communication meta analysis example.

4.1.13 Sample size

As stated in chapter 4.1.6, the only way to increase the power of a test is to increase the sample size. In the candy factory example, the sample size is the total number of candies in the bag. With only 10 candies in the bag, the power of the test is only 0.11. To reach our desired power of 80%, we clearly need to increase the sample size. In figure 4.14, we increased the number of candies in the bag to 15. We can see on the x-axis that the posible outcome space for the number of yellow candies in the bag is now 0 to 15. This of still assumes our \(H_0\) to be true, and the parameter of the machine is still \(\theta = .5\), half of the candies in the bag should be yellow. Though the parameter is still the same, the expected value when we have bags of 16 cancies is now \(.5 \times 20 = 10\), right in the middle of our distribution.

Figure 4.14 still follows the reasoning scheme we have setup earlier. We decide to reject \(H_0\) on the outside of our critical values (Red vertical line). We determined the position of the critical value based on our chosen alpha level. Becouse our outcome space is larger we can be more accurate in striving for an \(\alpha = .5\). Our alpha is now 4.1%, we get this by adding the yellow bars 0, 1, 2, 3, 4, 5 and 15 up unitil 20, under the null distribution. This is not exactly 5 percent, but shifting the critical value inwards, would make the alpha level to high. So, this is close enough.

With this sample size, we can acquire our desired power of 80%. If we would assume our alternative hypothesis to be true, our decision to reject the null when you get 5 or less yellow candies, would be correct 80% of the time. The power of 80% is the sum of the light yellow bars under the assumption that \(H_A\) is true on the outside of our critical value. So, the power is the probability of getting 0, 1, 2, 3 ,4 ,5 or 15, 16,17, 18, 19 ,20 yellow candies under the alternative distribution.

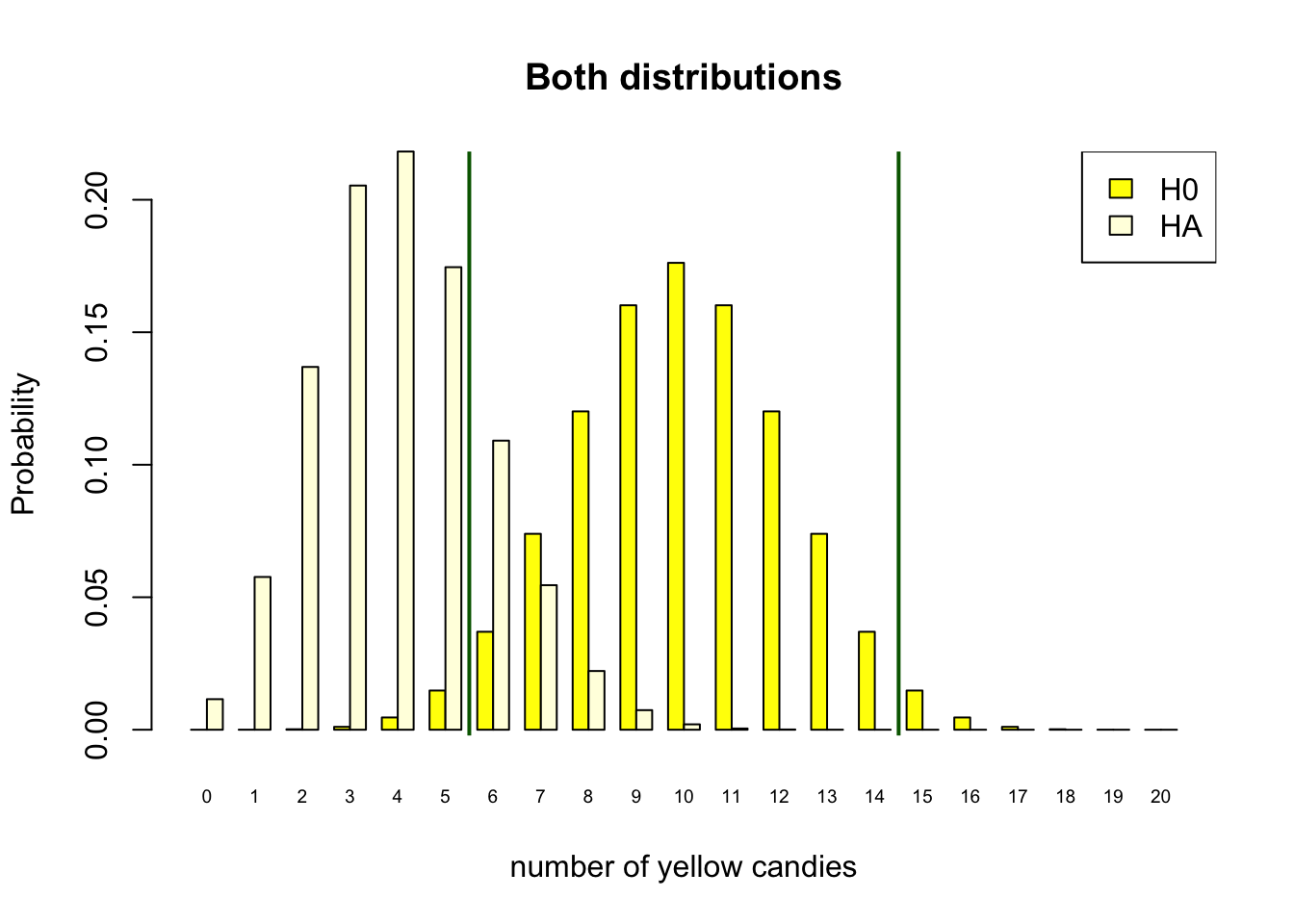
Figure 4.14: Discrete binomial distributions

The same reasoning is applied to the continuous case. Let’s revisit the candy weight example. We could have a null hypothesis that the average yellow candy weight is the same as the weight of all other candy colors. But if in reality the yellow candies would be heavier, let’s say with an effect size of .3, we would need to determine what sample size we would need to get a power of 80% and a alpha of 5%.

Figure 4.15 shows the relation between sample size, power, alhpa and effect size. You can play around with the sliders de determine what sample size you would need.

Figure 4.15: How does test power depend on effect size, type of test, significance level, and sample size? Sampling distributions of the sample mean under the null hypothesis (H₀, left-hand curve) and under the assumed true value of the population mean (H₁, right-hand curve) for a one-sample t test.

Just like the discrete case, we choose an alpha level, and we can see the critical value in the null distribution. The alpha level of 5% is the area under the curve of the null distributon on the outside of the critical values. The power is the area under the alternative distribution that is outside the critical values.

The reasoning is again the same as in the discrete case. We first determine our desired alpha and power, make sure our sample size is large enough to get the desired power, for our effect size of interest. Then, when we collect our data, we can calculate our test statistic and determine if we can reject the null hypothesis or not, being confident theat we will be wrong in our conclusion in 5% of the cases, and that we will be right in 80% of the cases when the alternative hypothesis is actually true.

4.1.13.1 How to determine sample size

As stated in chapter @ref(#power) about the power of a test, we already considered that we do not know the parameter for the alternative distribution and that we therefore also don’t know the true effect size. We stated that you can make an educated guess about the true effect size based on previous research, theory, or other empirical evidence.

In research you can take these assumptions into account by conducting a power analysis. A power analysis is a statistical method to determine the sample size you need to get a desired power for a given effect size.

It can be difficult to specify the effect size that we should expect or that is practically relevant. If there is little prior research comparable to our new project, we cannot reasonably specify an effect size and calculate sample size. Though, if there are meta analysis available for you research topic of interest or you have the effect sizes from a few previous studies, you can use GPower to calculate the sample size you need to get a desired power for a given effect size. GPower is a stand alone program that can be downloaded from the internet, and is specificly designed to calculate sample size for a wide range of statistical tests.

Download G*Power here

In GPower you can specify the test you want to conduct, the effect size you expect, the alpha level you want to use, and the power you want to achieve. GPower will then calculate the sample size you need to get the desired power for the given effect size.

For our candy color example, we can use G*Power to calculate the sample size we need to get a power of 80% for a given effect size of .3.

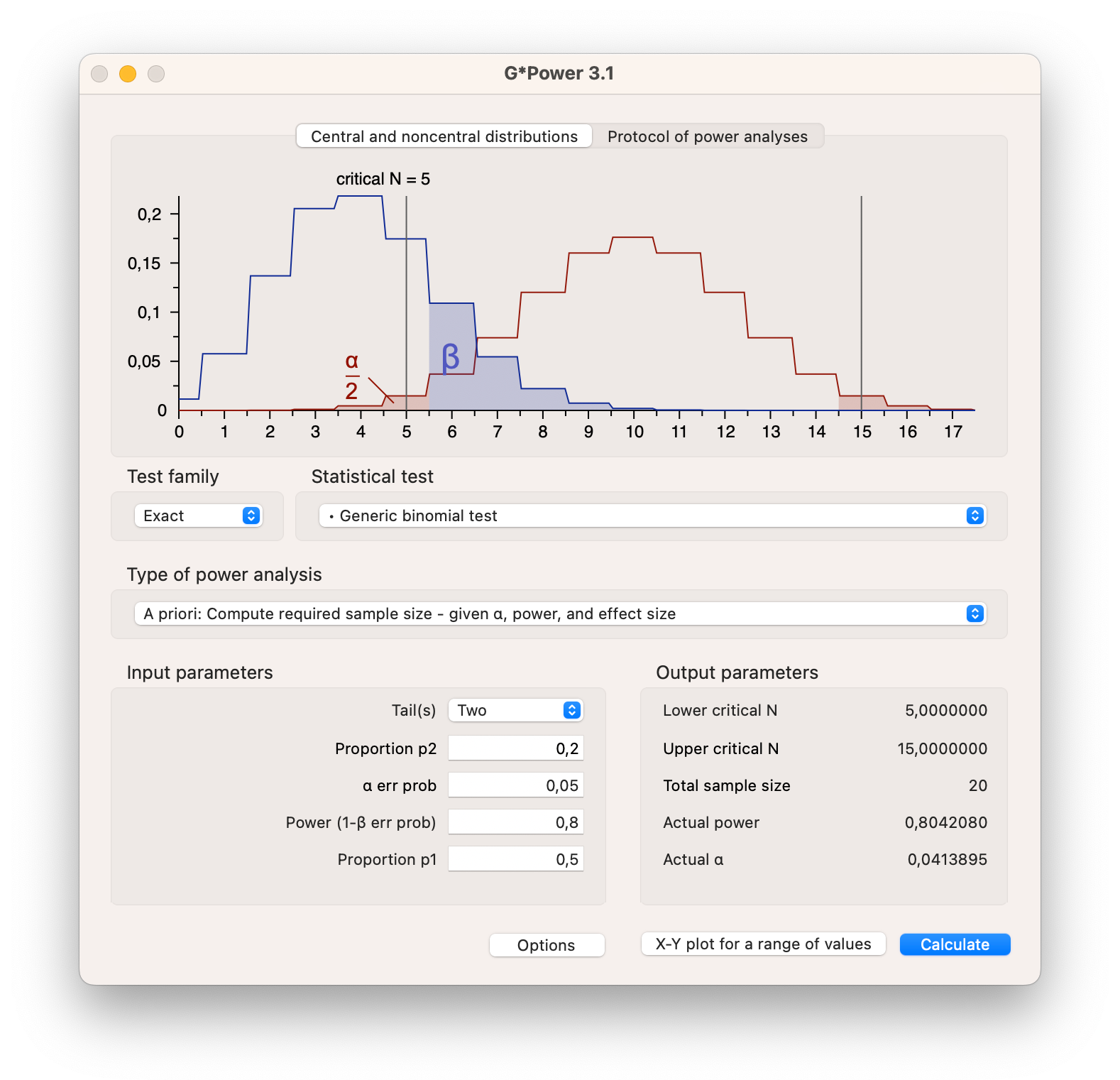
Figure 4.16: Power analysis in G*Power for a binomial distribution

In figure 4.16 you can see that for the binomial test we have set the proportion p1 to .5 (\(H_0\)) and the proportion p2 (\(H_A\)) to .2, indirectly setting the effect size to .3. We have set the alpha level to 5% and the power to 80%. By hitting the calculate button, G*Power will calculate the sample size we need. In this case we need 20 candies in the bag to get a power of 80%. The plot shows exactly the same information as in figure 4.14, though with lines instead of bars.

4.1.14 One-Sided and Two-Sided Tests

In the preceding section, you may have had some trouble when you were determining whether a research hypothesis is a null hypothesis or an alternative hypothesis. The research hypothesis stating that average media literacy is below 5.5 in the population, for example, represents the alternative hypothesis because it does not fix the hypothesized population value to one number. The accompanying null hypothesis must cover all other options, so it must state that the population mean is 5.5 or higher. But this null hypothesis does not specify one value as it should, right?

This null hypothesis is slightly different from the ones we have encountered so far, which equated the population value to a single value. If the null hypothesis equates a parameter to a single value, the null hypothesis can be rejected if the sample statistic is either too high or too low. There are two ways of rejecting the null hypothesis, so this type of hypothesis and test are called two-sided or two-tailed.

By contrast, the null hypothesis stating that the population mean is 5.5 or higher is a one-sided or one-tailed hypothesis. It can only be rejected if the sample statistic is at one side of the spectrum: only below (left-sided) or only above (right-sided) the hypothesized population value. In the media literacy example, the null hypothesis is only rejected if the sample mean is well below the hypothesized population value. A test of a one-sided null hypothesis is called a one-sided test.

Figure 4.17: One-sided and two-sided tests of a null hypothesis.

In a left-sided test of the media literacy hypothesis, the researcher is not interested in demonstrating that average media literacy among children can be larger than 5.5. She only wants to test if it is below 5.5, perhaps because an average score below 5.5 is alarming and requires an intervention, or because prior knowledge about the world has convinced her that average media literacy among children can only be lower than 5.5 on average in the population.

If it is deemed important to note values well over 5.5 as well as values well below 5.5, the research and null hypotheses should be two-sided. Then, a sample average well above 5.5 would also have resulted in a rejection of the null hypothesis. In a left-sided test, however, a high sample outcome cannot reject the null hypothesis.

4.1.14.1 Boundary value as hypothesized population value

Figure 4.18: Sampling distribution of average media literacy.

You may wonder how a one-sided null hypothesis equates the parameter of interest with one value as it should. The special value here is 5.5. If we can reject the null hypothesis stating that the population mean is 5.5 because our sample mean is sufficiently lower than 5.5, we can also reject any hypothesis involving population means higher than 5.5.

In other words, if you want to know if the value is not 5.5 or more, it is enough to find that it is less than 5.5. If it’s less than 5.5, then you know it’s also less than any number above 5.5. Therefore, we use the boundary value of a one-sided null hypothesis as the hypothesized value for the population in a one-sided test.

4.1.14.2 One-sided – two-sided distinction is not always relevant

Note that the difference between one-sided and two-sided tests is only useful if we test a statistic against one particular value or if we test the difference between two groups.

In the first situation, for example, if we test the null hypothesis that average media literacy is 5.5 in the population, we may only be interested in showing that the population value is lower than the hypothesized value. Another example is a test on a regression coefficient or correlation coefficient. According to the null hypothesis, the coefficient is zero in the population. If we only want to use a brand advertisement if exposure to the advertisement increases brand awareness among consumers, we apply a right-sided test to the coefficient for the effect of exposure on brand awareness because we are only interested in a positive effect (larger than the zero).

In the second situation, we compare the scores of two groups on a dependent variable. If we compare average media literacy after an intervention to media literacy before the intervention (paired-samples t test), we must demonstrate an increase in media literacy before we are going to use the intervention on a large scale. Again, a one-sided test can be applied.

In contrast, we cannot meaningfully formulate a one-sided null hypothesis if we are comparing three groups or more. Even if we expect that Group A can only score higher than Group B and Group C, what about the difference between Group B and Group C? If we can’t have meaningful one-sided null hypotheses, we cannot meaningfully distinguish between one-sided and two-sided null hypotheses.

4.1.14.3 From one-sided to two-sided p values and back again

Statistical software like SPSS usually reports either one-sided or two-sided p values. What if a one-sided p value is reported but you need a two-sided p value or the other way around?

In Figure 4.19, the sample mean is 3.9 and we have .015 probability of finding a sample mean of 3.9 or less if the null hypothesis is true. This probability is the surface under the curve to the left of the red line representing the sample mean. It is the one-sided p value that we obtain if we only take into account the possibility that the population mean can be smaller than the hypothesized value. We are only interested in the left tail of the sampling distribution.

Figure 4.19: Halve a two-sided p value to obtain a one-sided p value, double a one-sided p value to obtain a two-sided p value.

In a two-sided test, we have to take into account two different types of outcomes. Our sample outcome can be smaller or larger than the hypothesized population value. As a consequence, the p value must cover samples at opposite sides of the sampling distribution. We should not only take into account sample means that are smaller than 5.5 but also sample means that are just as much larger than the hypothesized population value. So our two-sided p value must include both the probability of .015 for the left tail and for the right tail of the distribution in Figure 4.19. We must double the one-sided p value to obtain the two-sided p value.

In contrast, if our statistical software tells us the two-sided p value and we want to have the one-sided p value, we can simply halve the two-sided p value. The two-sided p value is divided equally between the left and right tails. If we are interested in just one tail, we can ignore the half of the p value that is situated in the other tail. Of course, this only makes sense if a one-sided test makes sense.

Be careful if you divide a two-sided p value to obtain a one-sided p value. If your left-sided test hypothesizes that average media literacy is below 5.5 but your sample mean is well above 5.5, the two-sided p value can be below .05. But your left-sided test can never be significant because a sample mean above 5.5 is fully in line with the null hypothesis. Check that the sample outcome is at the correct side of the hypothesized population value.