10.1 Mediation as Causal Process

Figure 10.2: How does a common cause affect regression coefficients? The values in this path diagram represent standardized regression coefficients.

10.1.1 Criteria for a causal relation

Researchers are usually interested in causal effects, so let us theorize a causal order between age and reading newspapers. From previous research and personal experience, we strongly suspect that older people spend more time on reading newspapers than young people. In statistical language, we expect a positive correlation between age and newspaper reading time. Can age be a cause of current newspaper reading?

Correlation is the first criterion. A causal relation implies correlation or another type of statistical association. If newspaper reading is not correlated with age, it is hard to imagine that age affects newspaper reading. But correlation does not imply causation, as the saying goes. Correlated variables do not have to be causally related. We need additional arguments to add plausibility to a causal relation.

The second criterion is the time order between cause and consequence. A cause must appear before the consequence. In our example, a person’s age must be fixed before she displays the behaviour that we want to explain, namely reading newspapers. The time order is very plausible here because age stands for the moment a person was born, which must be prior in time to reading newspapers. If there is a causal relation between age and reading newspapers, age must be the cause and newspaper reading the consequence.

A third criterion for causality is that the correlation is not spurious. In Section 9.3.2, we have encountered a spurious effect as an effect that incorrectly includes the effect of a confounder (reinforcer).

In the context of causality, spuriousness is linked to a confounder that is a common cause to both the assumed cause (predictor) and consequence (dependent variable). Age, for instance, can be a common cause both to having (grand)children and reading newspapers. Older people tend to have more (grand)children and they read more newspapers. If we do not control for age in a regression model predicting newspaper reading time from the number of (grand)children a person has, we may find a positive effect.

This effect is probably not causal: We do not spend more time reading newspapers because we have more (grand)children. Unless we use newspaper reading to ignore our children and grandchildren when they are around. Most if not all of the effect of (grand)children on newspaper reading is spurious because it results from a common cause, namely age or the habits and opportunities represented by age.

To interpret an effect that we find as causal, then, we must ensure that there are no confounding variables that are common causes to both our predictors and dependent variable. Including them as controls in the regression model is a way to solve the problem (Chapter 9). With non-experimental data, for example data on newspaper reading habits gathered in a survey, we cannot be sure that we have included all common causes in our model. In this situation, we should always keep in mind that the effects that we find may be caused by variables not included in our regression model. In an experiment, however, we can use experimental randomization to minimize the chance of having any confounders at all (Section 9.2.3).

10.1.2 Mediation as indirect effect

A common cause does not have to remove the entire effect between a predictor and dependent variable. Even if part of newspaper reading is caused by age, another part can be caused by a variable related to age, for example, interest in politics. During their lifetime, people may gain more experience with politics and, for that reason, become more interested in reading about politics. This may cause them to invest more time in reading newspapers for collecting information.

Not all people become more interested in politics as they grow older and their interest in politics does not have to increase regularly during all of their lifetime. The relation between age and interest in politics, therefore, will not be perfect. This allows us to technically distinguish between the effect of age and the effect of interest in politics.

If we include both age and interest in politics as predictors in a regression model for newspaper reading time, the partial effect (Section 9.1.1) of interest in politics is corrected for the spurious correlation between interest in politics and newspaper reading caused by age as their common cause. The partial effect of political interest can be interpreted as causal if current interest in politics was attained before the newspaper readings that we measure (very plausible) and age is the only common cause of interest in politics and newspaper reading (highly questionable).

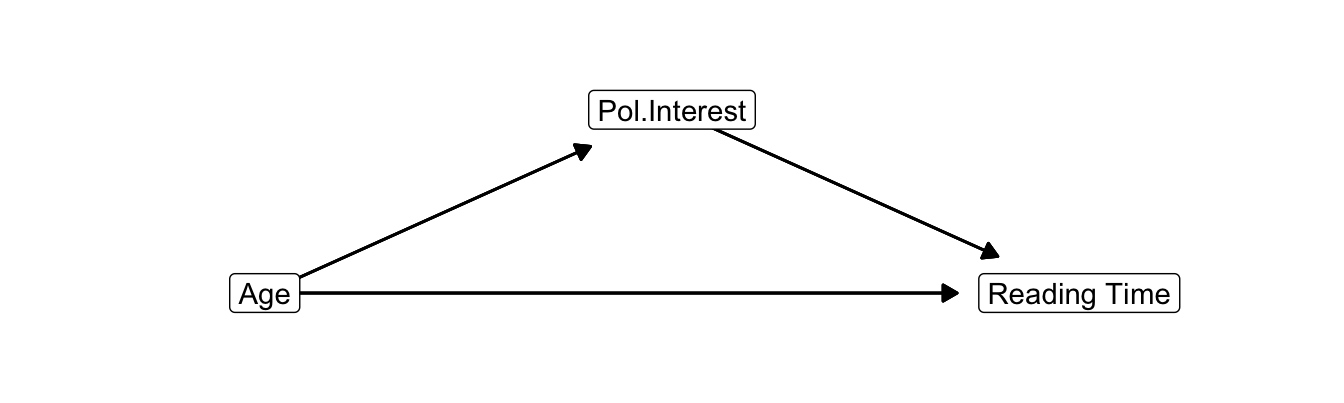
Figure 10.3: Causal diagram for the effects of age and interest in politics on newspaper reading time.

Now let us draw the causal diagram for this simple example (Figure 10.3). A causal diagram contains the names of the variables with arrows pointing from causes to consequences. The causal order of variables is represented from left to right. In Figure 10.3, the very first cause (age) is at the left, the final consequence (newspaper reading time) is at the right, and interest in politics is placed in the middle. In this layout, the arrows always point to the right.

In the causal order that we theorize, age is causally prior (antecedent) to interest in politics, which is causally prior to current newspaper reading time. We have an indirect effect of age on newspaper reading by way of interest in politics. When adults grow older, they tend to be more interested in politics and because of this, they tend to spend more time on reading newspapers. We say that interest in politics mediates the effect of age on newspaper reading time. Interest in politics is a mediator, an intermediary variable, or an intervening variable in this causal diagram.

A causal diagram like Figure 10.3 is also called a path diagram. Each indirect effect is a sequence of direct effects. Each direct effect is a “step” from one variable to another variable, represented by an arrow. An indirect effect, then, can be regarded as a path that we can follow to “travel” from one variable to another variable.

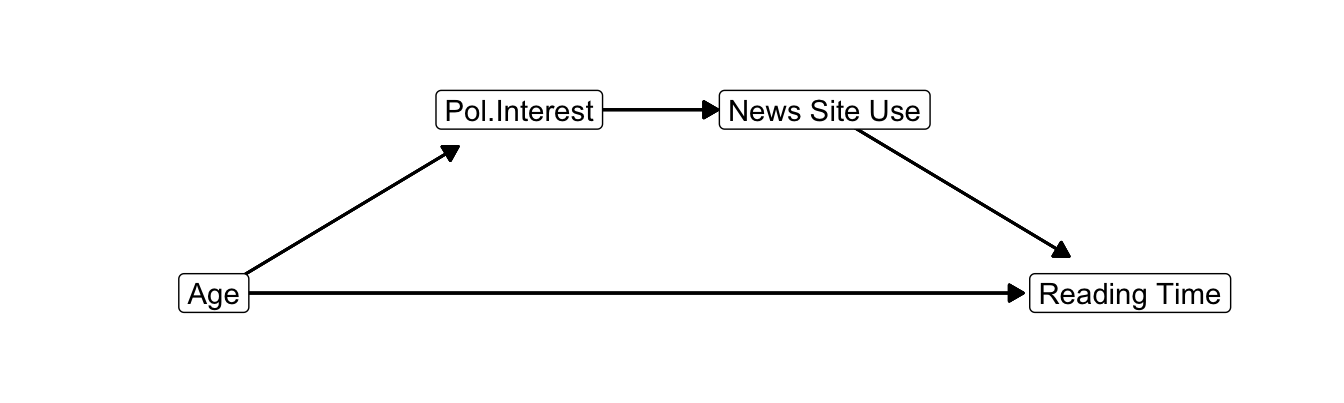
Figure 10.4: Causal diagram for the effect of age on newspaper reading time mediated by interest in politics and news site use.

An indirect effect may contain more than one step or mediator. If we include news site use in the model (Figure 10.4), we would have an indirect effect of age via interest in politics via news site use on newspaper reading time.

• Mediation: A causal relationship between a predictor, one or more mediators, and an outcome variable.
• Indirect effect: An effect in which three (or more) variables affect each other in a causal order: the predictor affects the mediator, the mediator affects another mediator or the outcome variable.

10.1.3 Causal process

In our example (Figure 10.4), age has a direct effect on newspaper reading time. What does the direct effect mean? If we start thinking about why older people spend more time on reading newspapers, we soon realize that this is probably not some biological process. It is hard to believe that an ageing human body requires more newspaper reading time. The effect is more likely to be social.

In the middle of the 20th century, newspapers were among the most important sources of information. A person who was born and grew up in that period is accustomed to using newspapers as main information source. For later generations, however, news sites on the internet have become important sources of information. Newspapers being less important to them, they are less oriented and accustomed to reading newspapers.

This line of reasoning shows us two things. First, we discover that our common cause may actually represent different things. Age, for instance, refers to life experience in its effect on interest in politics. In contrast, it relates to the period of coming of age in its direct effect on newspaper reading time.

Our second discovery is that we usually look for mediators if we want to understand a direct effect. Date of birth affects exposure to people using newspapers as information sources, which affects the habit of reading newspapers, which finally affects the time spent on reading newspapers later on. Exposure and habit are mediators here. A direct effect of age on newspaper reading represents a causal process that may contain many intermediary steps. Adding mediators to our model is a way of getting more insight in the causal process.