Null Hypothesis Testing

Klinkenberg

University of Amsterdam

12 sep 2022

Null Hypothesis
Significance Testing

Neyman-Pearson Paradigm

Neyman - Pearson

Two hypothesis

\(H_0\)

  • Skeptical point of view
  • No effect
  • No preference
  • No Correlation
  • No difference

\(H_A\)

  • Refute Skepticism
  • Effect
  • Preference
  • Correlation
  • Difference

Frequentist probability

  • Objective Probability
  • Relative frequency in the long run

Standard Error

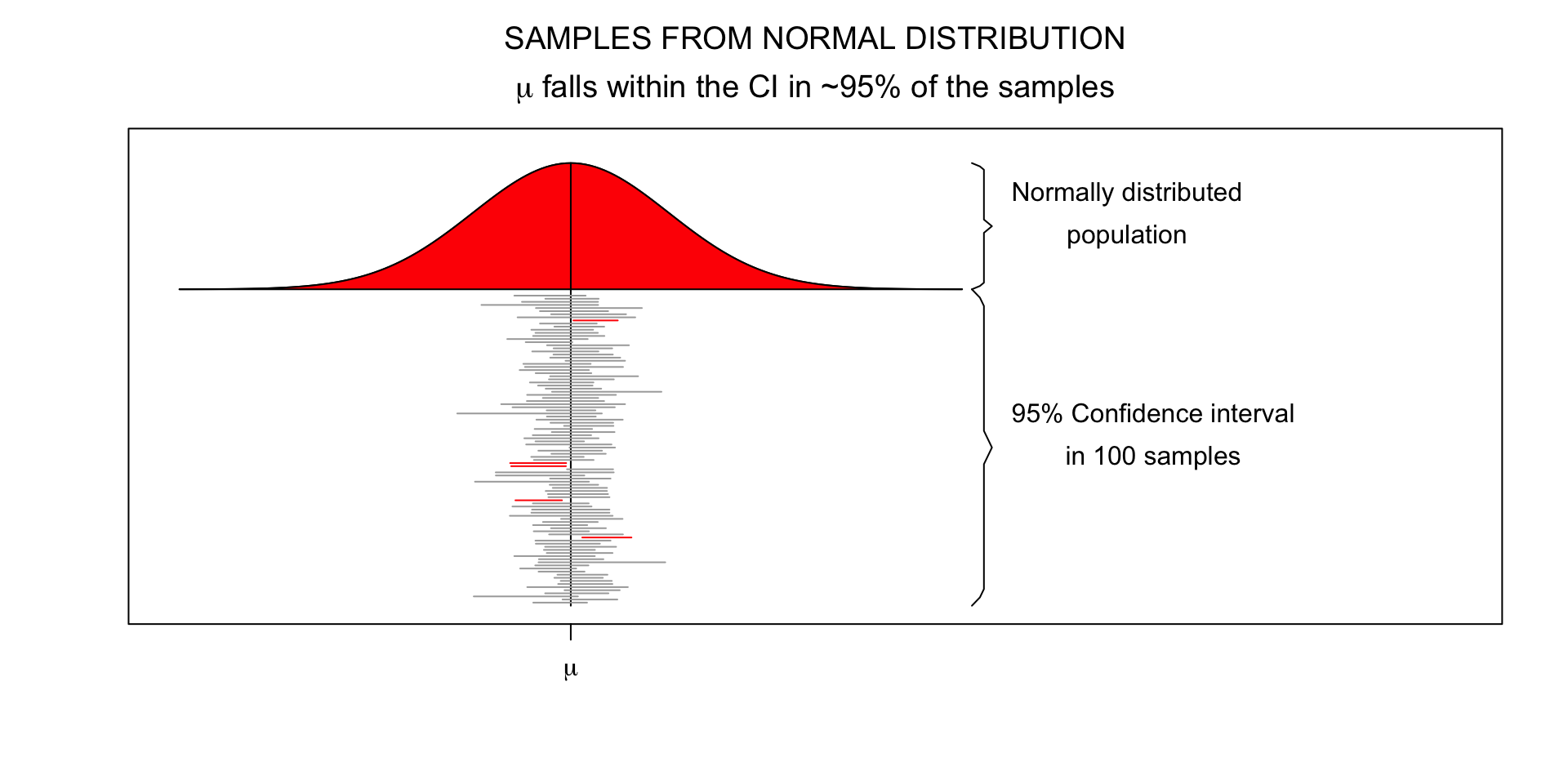
95% confidence interval

\[SE = \frac{\text{Standard deviation}}{\text{Square root of sample size}} = \frac{s}{\sqrt{n}}\]

  • Lowerbound = \(\bar{x} - 1.96 \times SE\)
  • Upperbound = \(\bar{x} + 1.96 \times SE\)

Standard Error

Your browser does not support the canvas element.

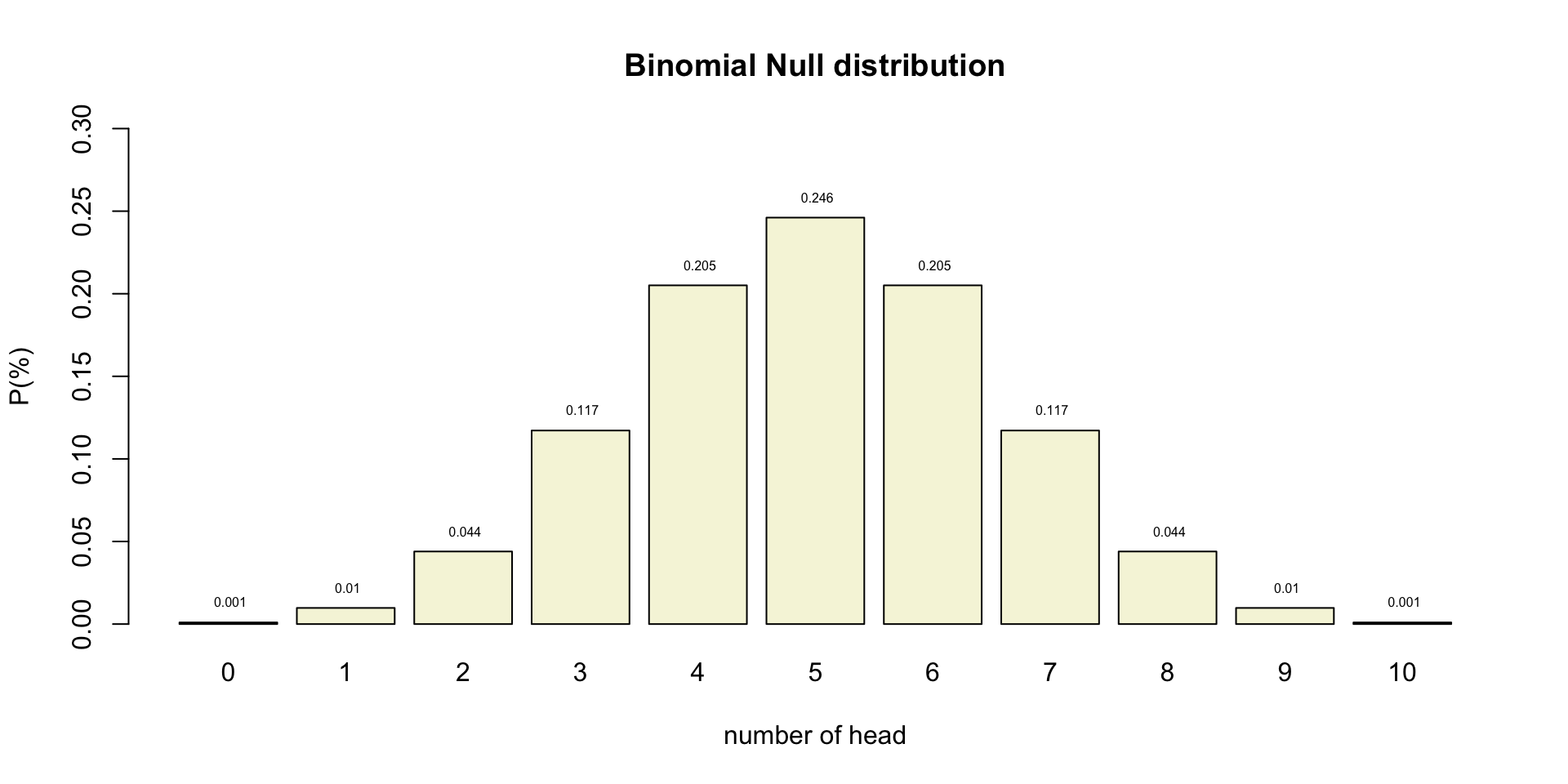
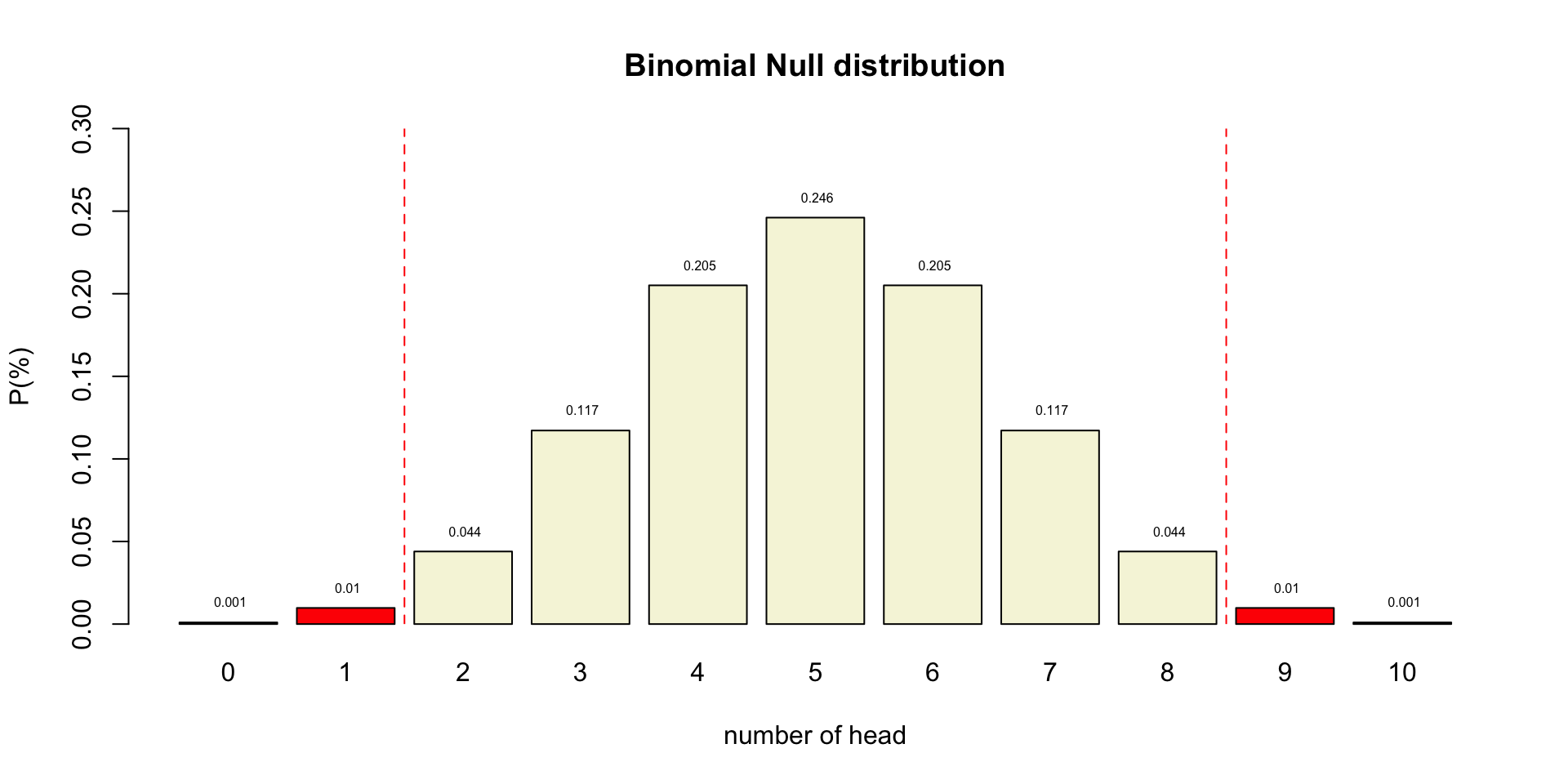
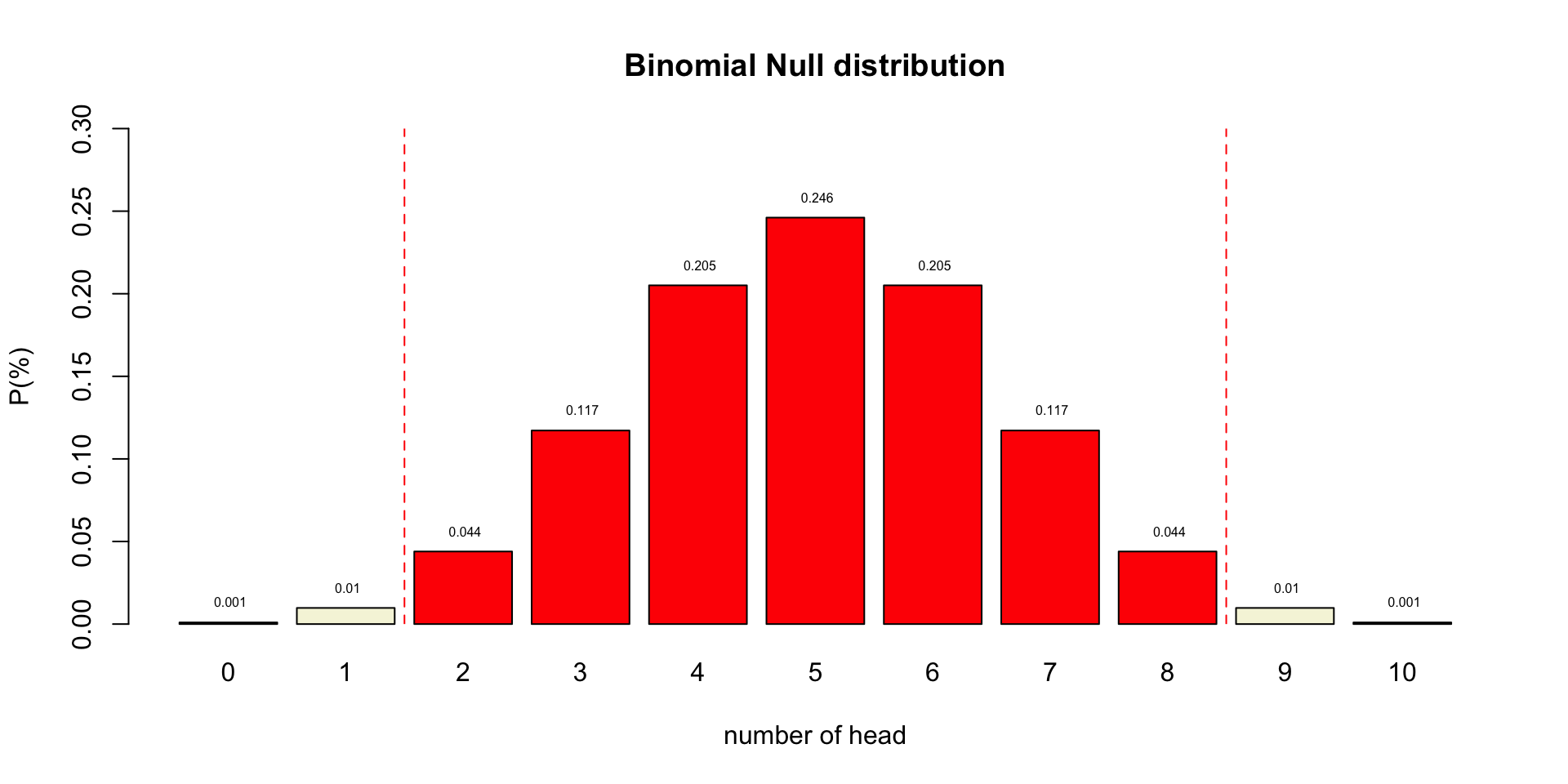
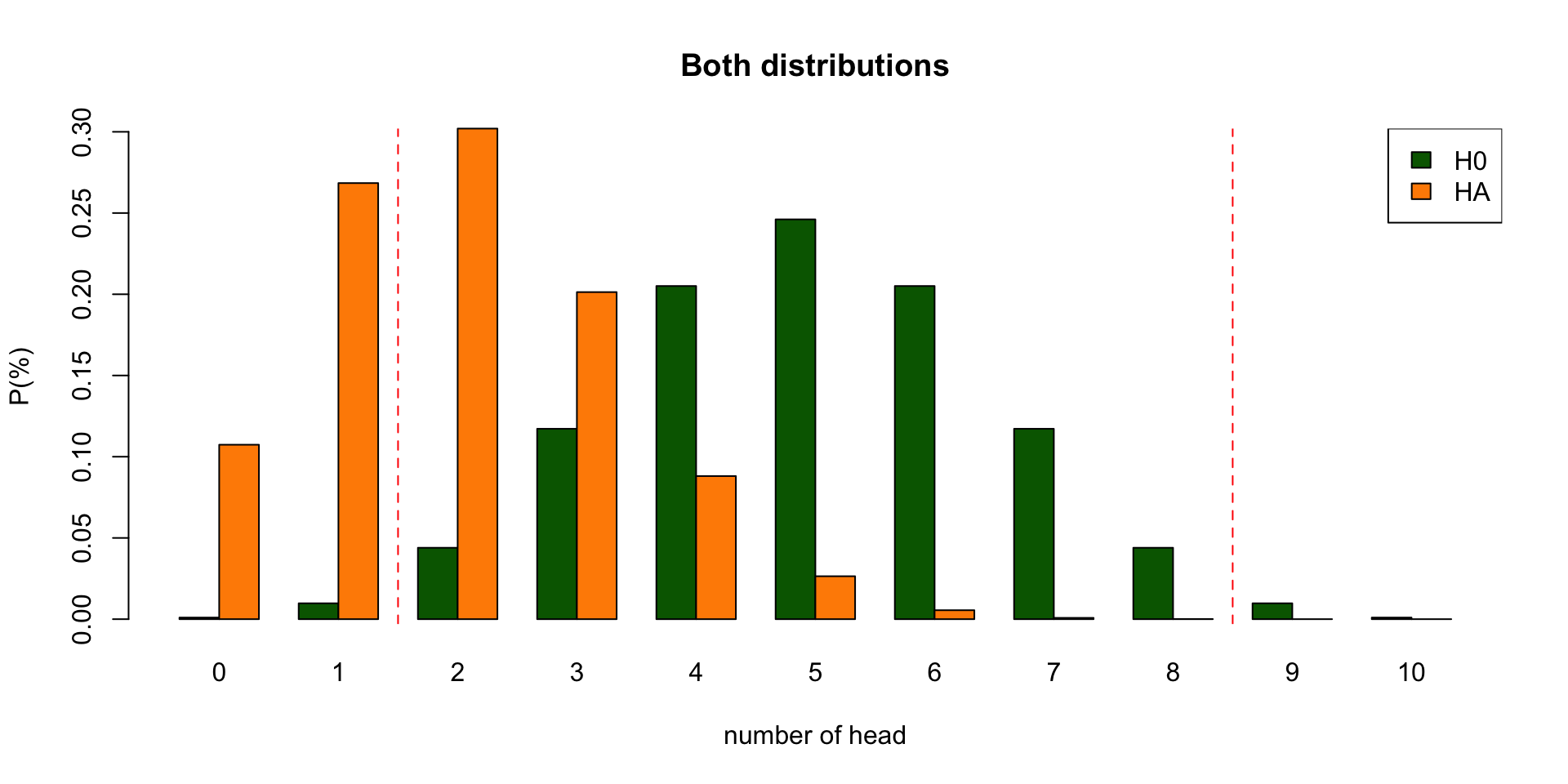
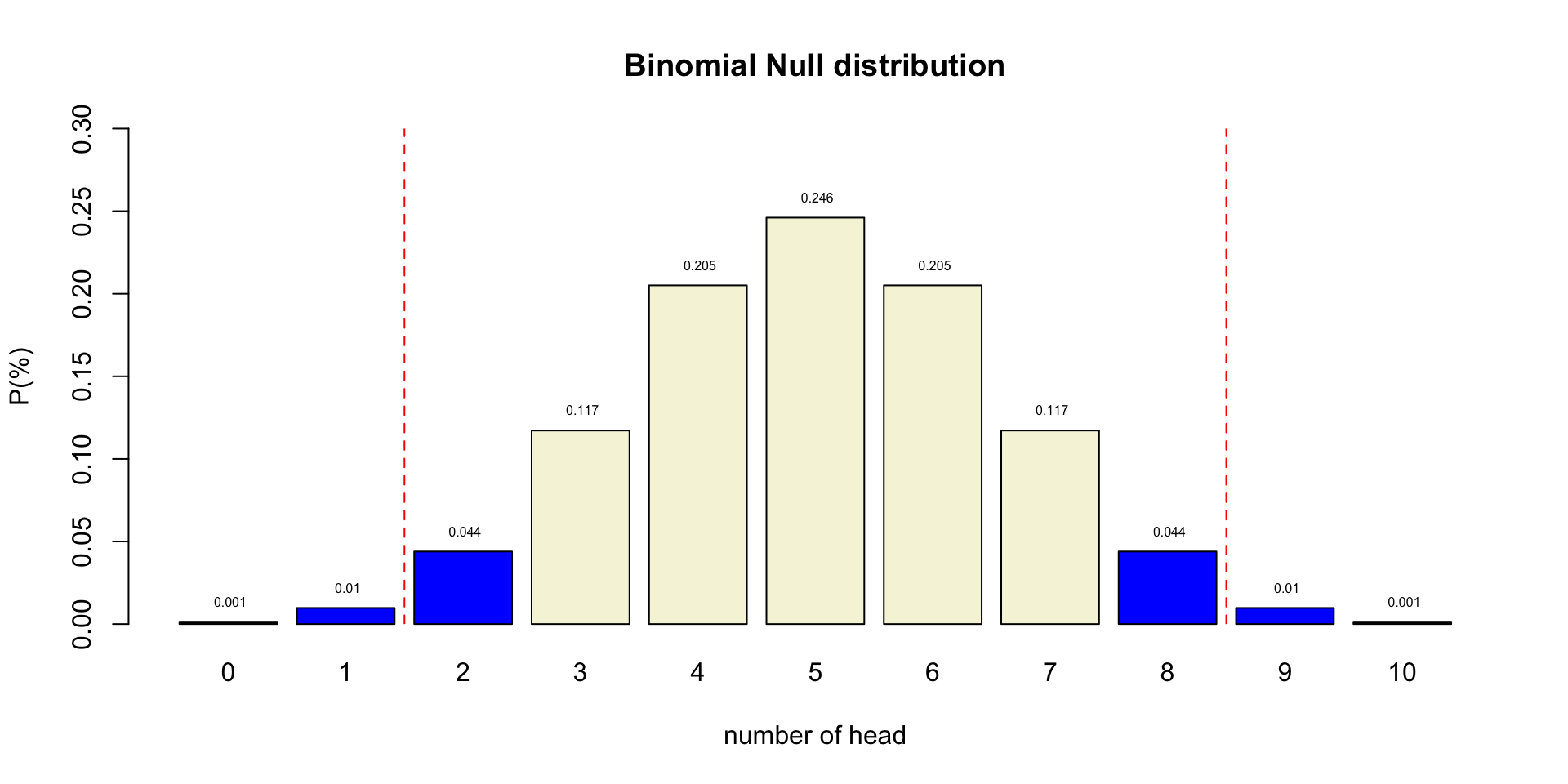
Binomial \(H_0\) distribution

n = 10   # Sample size
k = 0:n  # Discrete probability space
p = .5   # Probability of head

munt = 0:1

permutations = factorial(n) / ( factorial(k) * factorial(n-k) )
# permutations

p_k  = p^k * (1-p)^(n-k)  # Probability of single event
p_kp = p_k * permutations # Probability of event times 
                          # the occurrence of that event

title = "Binomial Null distribution"

# col=c(rep("red",2),rep("beige",7),rep("red",2))

barplot( p_kp, 
         main=title, 
         names.arg=0:n, 
         xlab="number of head", 
         ylab="P(%)", 
         col='beige',
         ylim=c(0,.3) )

# abline(v = c(2.5,10.9), lty=2, col='red')

text(.6:10.6*1.2,p_kp,round(p_kp,3),pos=3,cex=.5)

Binomial \(H_0\) distribution

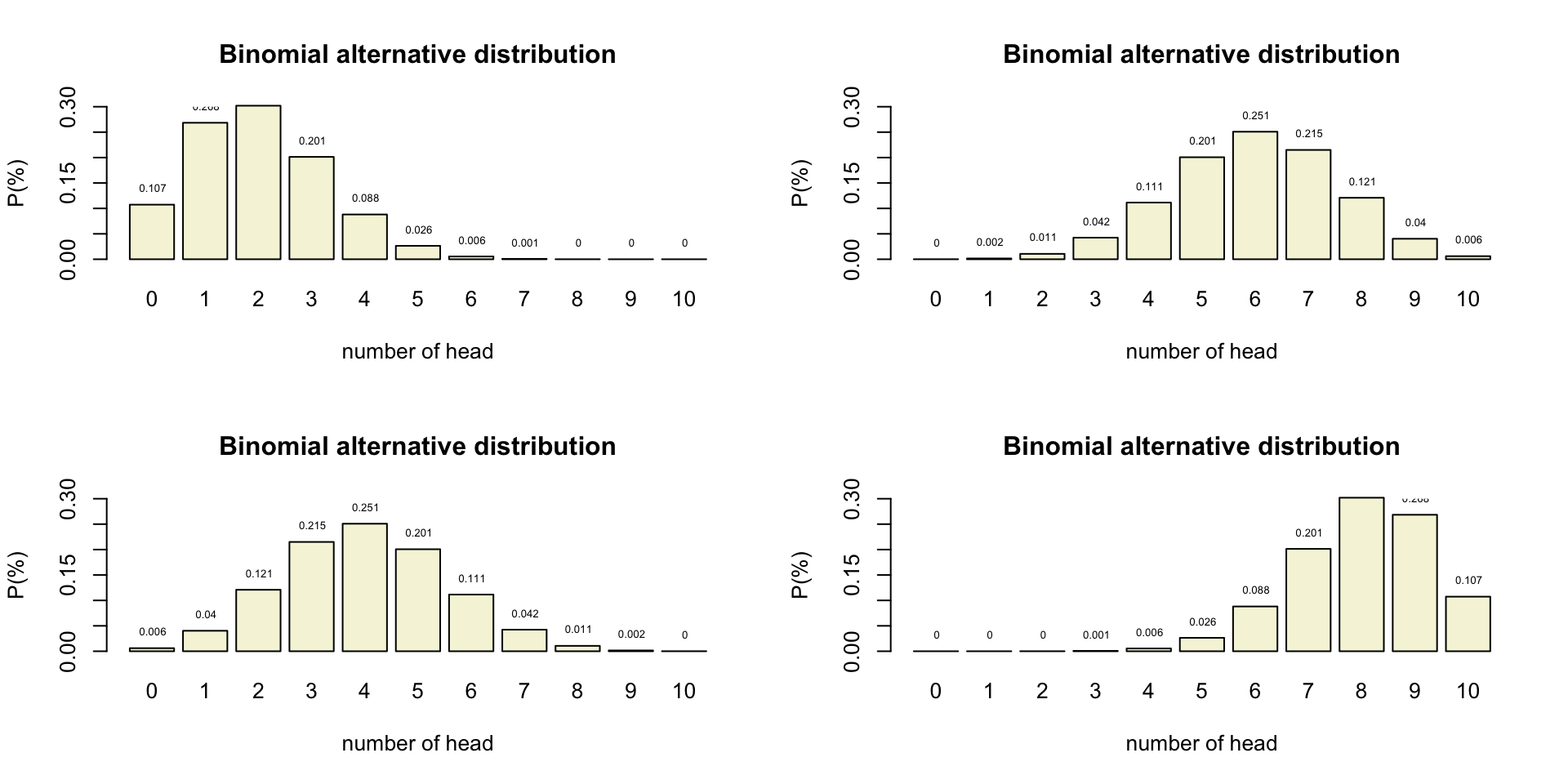
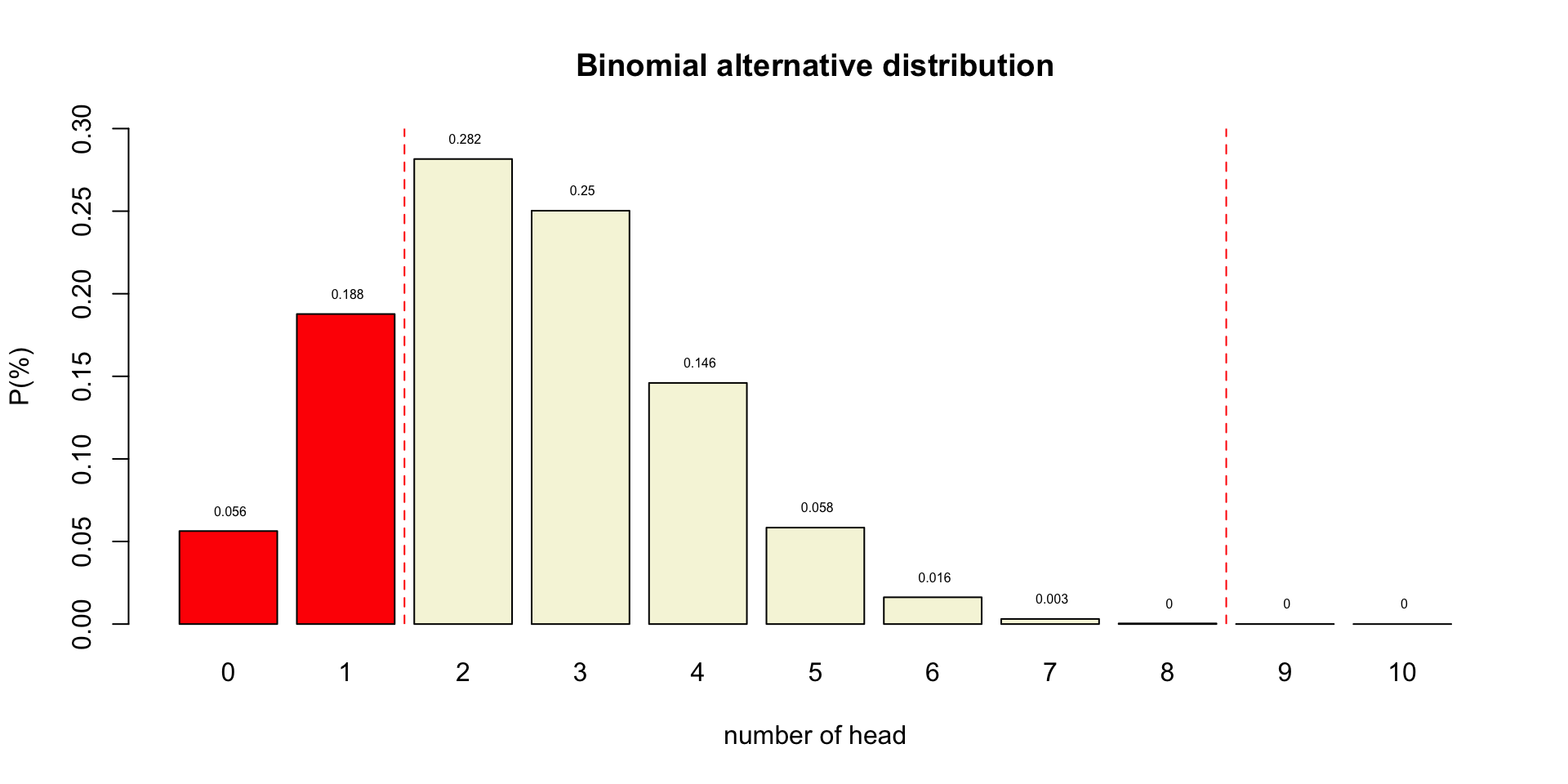
Binomial \(H_A\) distributions

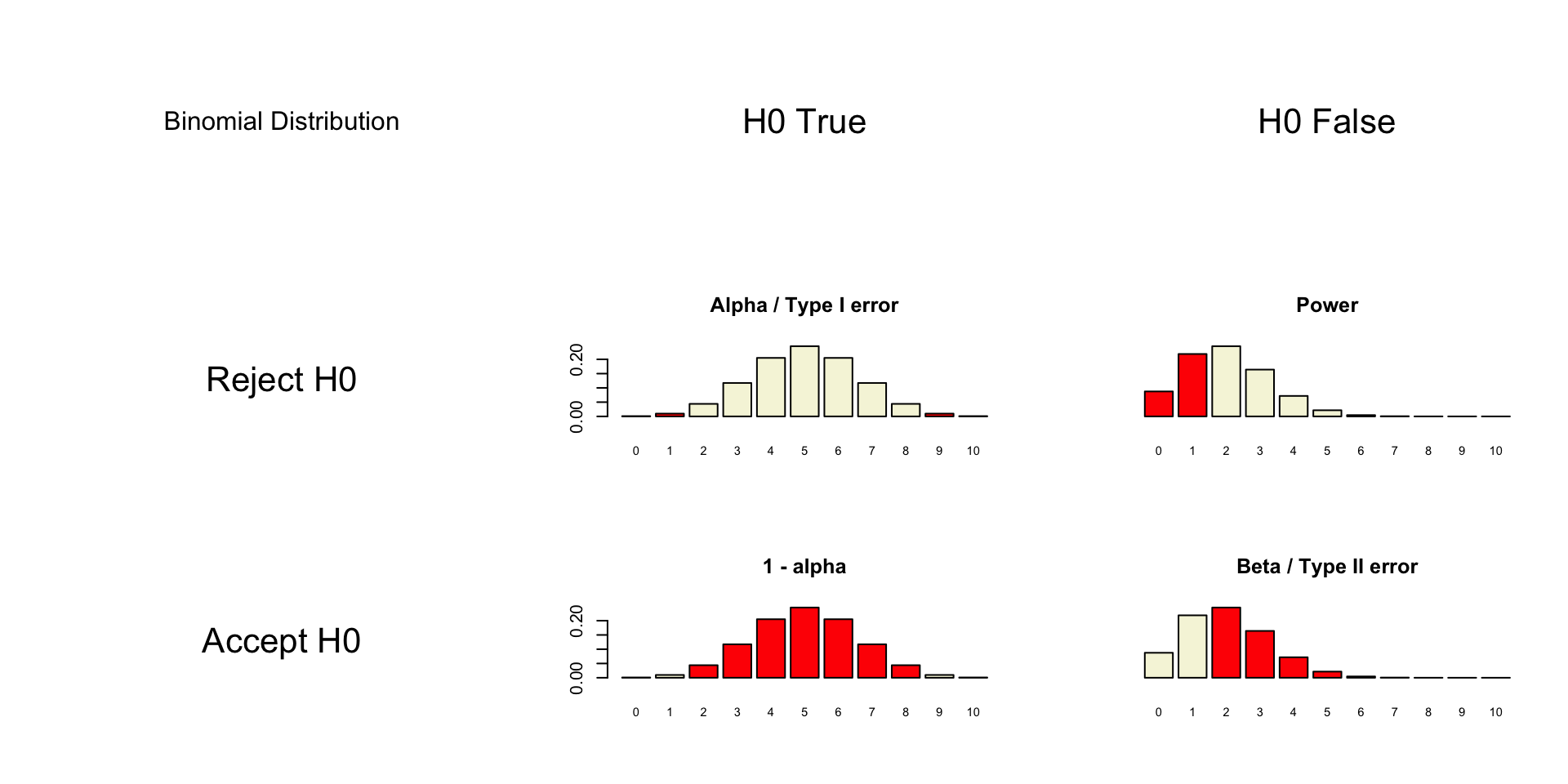
Decision table

H0 = TRUE H0 = FALSE Decide to reject H0 Decide to not reject H0 Alpha α Beta β 1 - α Power 1 - β

Alpha \(\alpha\)

  • Incorrectly reject \(H_0\)
  • Type I error
  • False Positive
  • Criteria often 5%
  • Distribution depends on sample size
H0 = TRUE H0 = FALSE Decide to reject H0 Decide to not reject H0 Alpha α Beta β 1 - α Power 1 - β

Power

  • Correctly reject \(H_0\)
  • True positive
  • Power equal to: 1 - Beta
    • Beta is Type II error
  • Criteria often 80%
  • Depends on sample size
H0 = TRUE H0 = FALSE Decide to reject H0 Decide to not reject H0 Alpha α Beta β 1 - α Power 1 - β

Post-Hoc Power

  • Also known as: observed, retrospective, achieved, prospective and a priori power
  • Specificly meaning:

The power of a test assuming a population effect size equal to the observed effect size in the current sample.

Source: O’Keefe (2007)

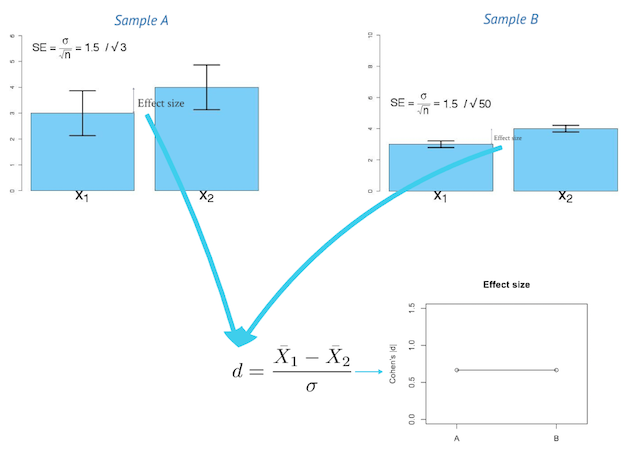
Effect size

In statistics, an effect size is a quantitative measure of the strength of a phenomenon. Examples of effect sizes are the correlation between two variables, the regression coefficient in a regression, the mean difference and standardised differences.

For each type of effect size, a larger absolute value always indicates a stronger effect. Effect sizes complement statistical hypothesis testing, and play an important role in power analyses, sample size planning, and in meta-analyses.

Source: WIKIPEDIA

Effect size

One minus alpha

  • Correctly accept \(H_0\)
  • True negative
H0 = TRUE H0 = FALSE Decide to reject H0 Decide to not reject H0 Alpha α Beta β 1 - α Power 1 - β

Beta

  • Incorrectly accept \(H_0\)
  • Type II error
  • False Negative
  • Criteria often 20%
  • Distribution depends on sample size
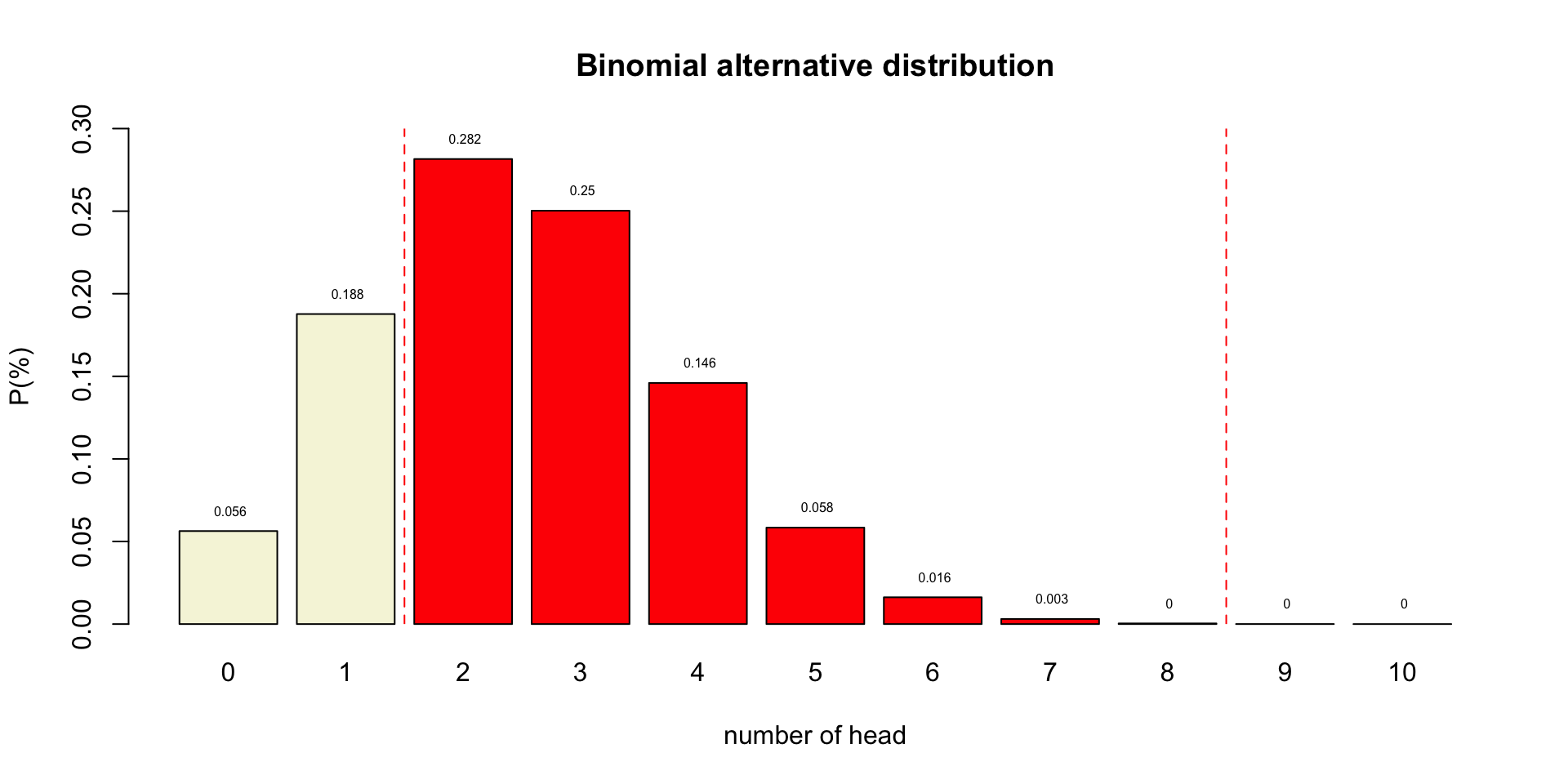
H0 = TRUE H0 = FALSE Decide to reject H0 Decide to not reject H0 Alpha α Beta β 1 - α Power 1 - β

P-value

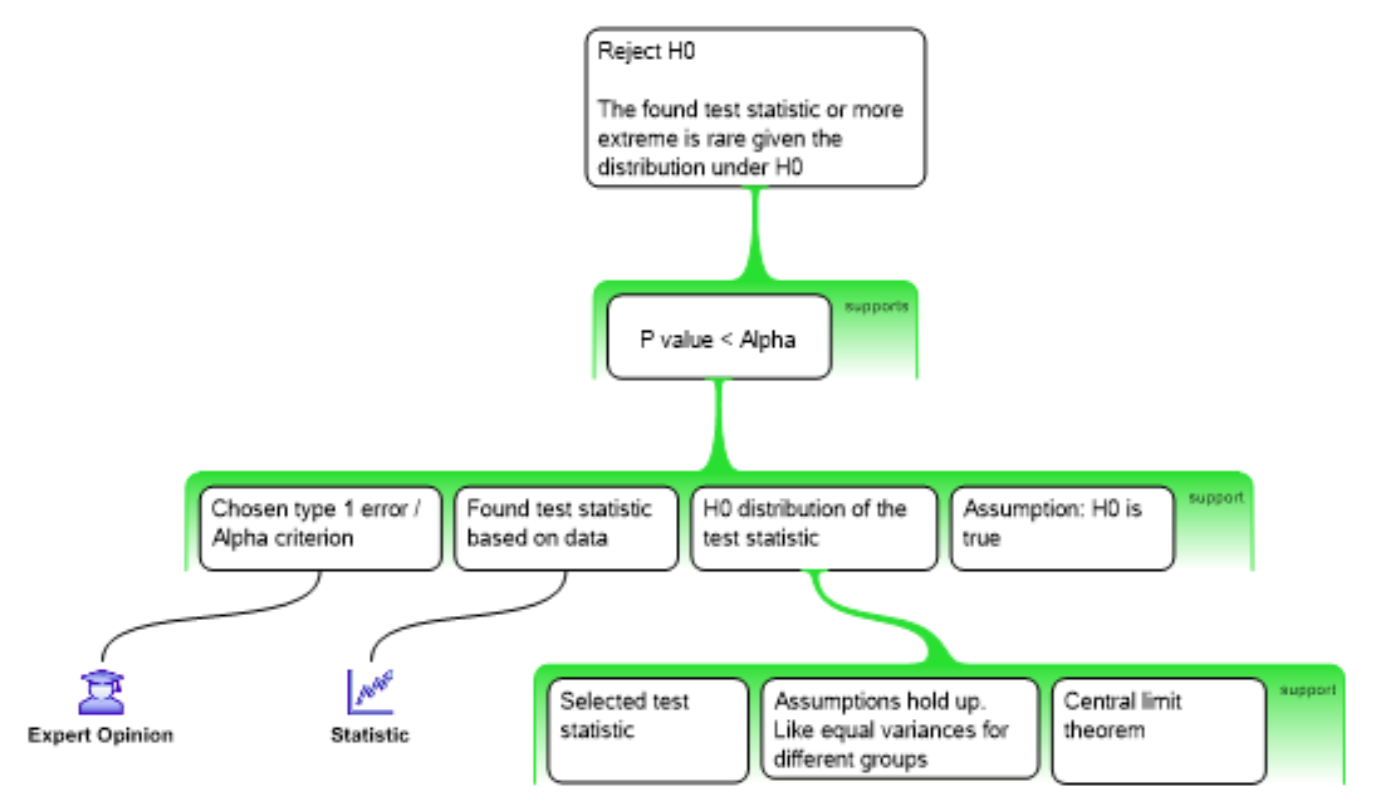
Conditional probability of the found test statistic or more extreme assuming the null hypothesis is true.

Reject \(H_0\) when:

  • \(p\)-value \(\leq\) \(alpha\)

P-value in \(H_{0}\) distribution

Test statistics

Some common test statistics

  • Number of heads
  • Sum of dice
  • Difference
  • \(t\)-statistic
  • \(F\)-statistic
  • \(\chi^2\)-statistic
  • etc…

Decision Table

N     = 10  # Sample size
H0    = .5  # Probability of head under H0 50/50
HA    = .2  # Aternative expected value
alpha = .05 # Selected type I error

# Color areas red for selected alpha
area <- dbinom(0:N, N, H0) < alpha/2

# barplot(dbinom(0:N,N, HA)) -> x.values

# x.values
# lb <- x.values[c(qbinom(alpha/2, N+1, H0), qbinom(alpha/2, N+1, H0)+1 )]
# ub <- x.values[c(qbinom(1-(alpha/2), N+1, H0), qbinom(1-(alpha/2), N+1, H0)+1 )]
# 
# mlb <- mean(lb)
# mub <- mean(ub)

col = rep("beige", N+1)
col[area] = "red"

col2 = rep("red", N+1)
col2[area] = "beige"

# Delete # to not color the plots
# col = col2  = "beige"

layout(matrix(1:9,3,3, byrow=T))

plot.new()
text(0.5,0.5,"Binomial Distribution",cex=1.5)
# text(0.5,0.1,paste("N:",N),cex=1.5)

plot.new()
text(0.5,0.5,"H0 True",cex=2)

plot.new()
text(0.5,0.5,"H0 False",cex=2)

plot.new()
text(0.5,0.5,"Reject H0",cex=2)

barplot(dbinom(0:N,N, H0), 
        col  = col, 
        # yaxt = 'n', 
        main = 'Alpha / Type I error', 
        names.arg = 0:N, 
        cex.names = 0.7)


# abline(v = mlb, col="red", lwd=3, lty=2)
# abline(v = mub, col="red", lwd=3, lty=2)

barplot(dbinom(0:N,N, HA), 
        col  = col, 
        yaxt = 'n', 
        main = 'Power', 
        names.arg = 0:N, 
        cex.names = 0.7)

plot.new()
text(0.5,0.5,"Accept H0",cex=2)

barplot(dbinom(0:N,N, H0), 
        col  = col2, 
        # yaxt = 'n', 
        main = '1 - alpha', 
        names.arg = 0:N, 
        cex.names = 0.7)

barplot(dbinom(0:N,N, HA), 
        col  = col2, 
        yaxt = 'n', 
        main = 'Beta / Type II error', 
        names.arg = 0:N, 
        cex.names = 0.7)

Decision Table

Reasoning Scheme

R<-PSYCHOLOGIST

Interactive distributions app by Kristoffer Magnusson

End

Contact

CC BY-NC-SA 4.0

Wetenschapsfilosofie & Statistisch Redeneren