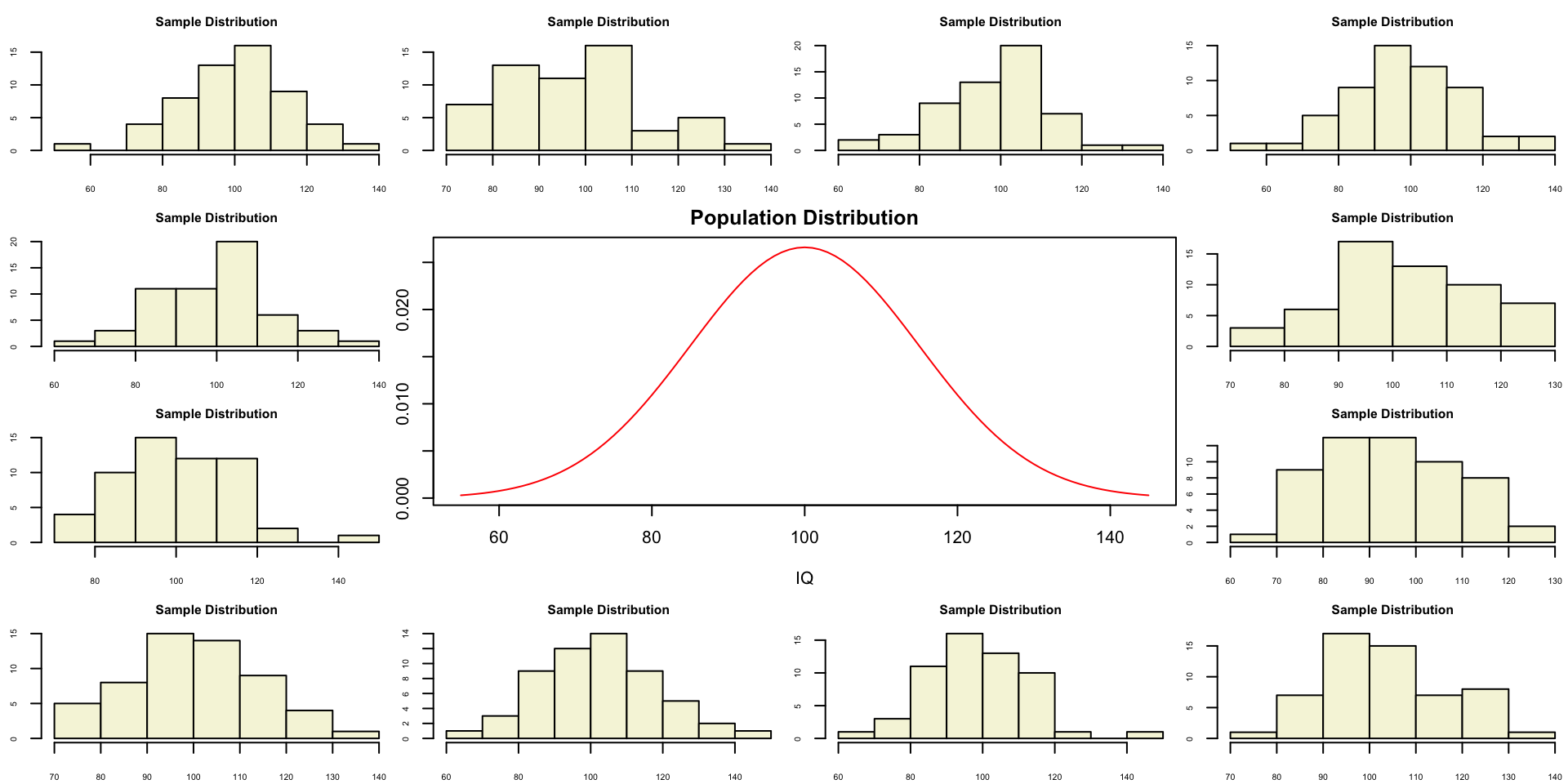
layout(matrix(c(2:6,1,1,7:8,1,1,9:13), 4, 4))
n = 56 # Sample size
df = n - 1 # Degrees of freedom
mu = 100
sigma = 15
IQ = seq(mu-45, mu+45, 1)
par(mar=c(4,2,2,0))
plot(IQ, dnorm(IQ, mean = mu, sd = sigma), type='l', col="red", main = "Population Distribution")
n.samples = 12
for(i in 1:n.samples) {
par(mar=c(2,2,2,0))
hist(rnorm(n, mu, sigma), main="Sample Distribution", cex.axis=.5, col="beige", cex.main = .75)
}T-distribution &
Multiple regression
Klinkenberg
University of Amsterdam
20 sep 2022
T-distribution
Gosset

In probability and statistics, Student’s t-distribution (or simply the t-distribution) is any member of a family of continuous probability distributions that arises when estimating the mean of a normally distributed population in situations where the sample size is small and population standard deviation is unknown.
In the English-language literature it takes its name from William Sealy Gosset’s 1908 paper in Biometrika under the pseudonym “Student”. Gosset worked at the Guinness Brewery in Dublin, Ireland, and was interested in the problems of small samples, for example the chemical properties of barley where sample sizes might be as low as 3.
Source: Wikipedia
Population distribution
Population distribution
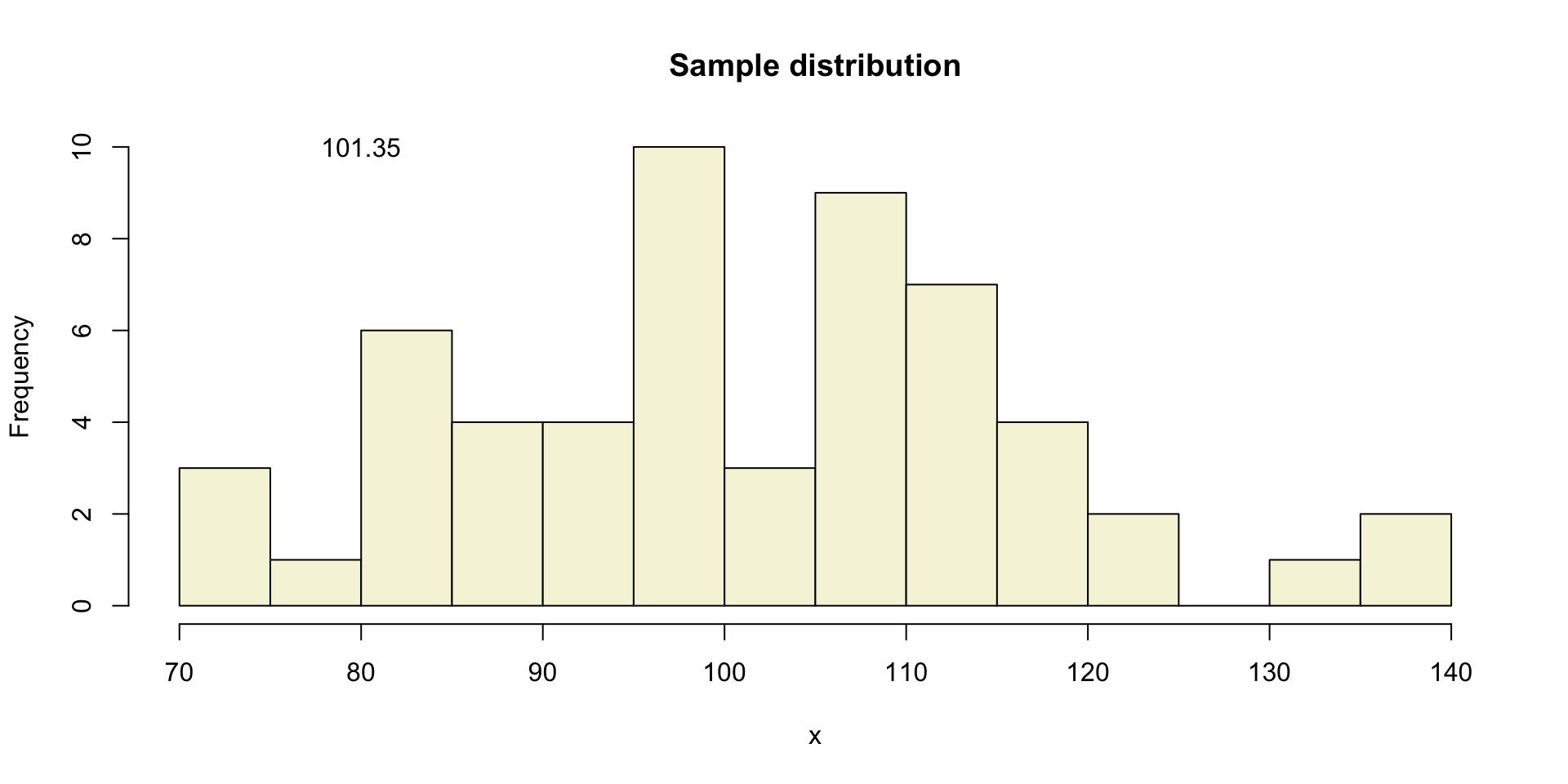
A sample
Let’s take one sample from our normal populatiion and calculate the t-value.
[1] 105.97091 97.88795 96.59252 101.97494 114.81159 123.34823 105.39531
[8] 86.35303 84.49523 80.42120 86.31988 118.64665 100.35848 137.86111
[15] 114.91078 80.79485 90.37722 136.44031 123.64622 99.29570 134.74928
[22] 108.68651 96.77961 107.46039 105.73403 100.95100 86.91514 75.50513
[29] 109.02407 84.63182 114.97081 92.17397 115.11011 114.97649 105.30372
[36] 95.37380 71.99298 109.96248 112.74284 70.13382 72.16366 95.65371
[43] 109.27013 83.50502 113.53344 93.60204 98.88010 114.53777 97.82642
[50] 93.81316 99.32199 85.80533 118.89700 83.79097 96.21963 119.69839A sample
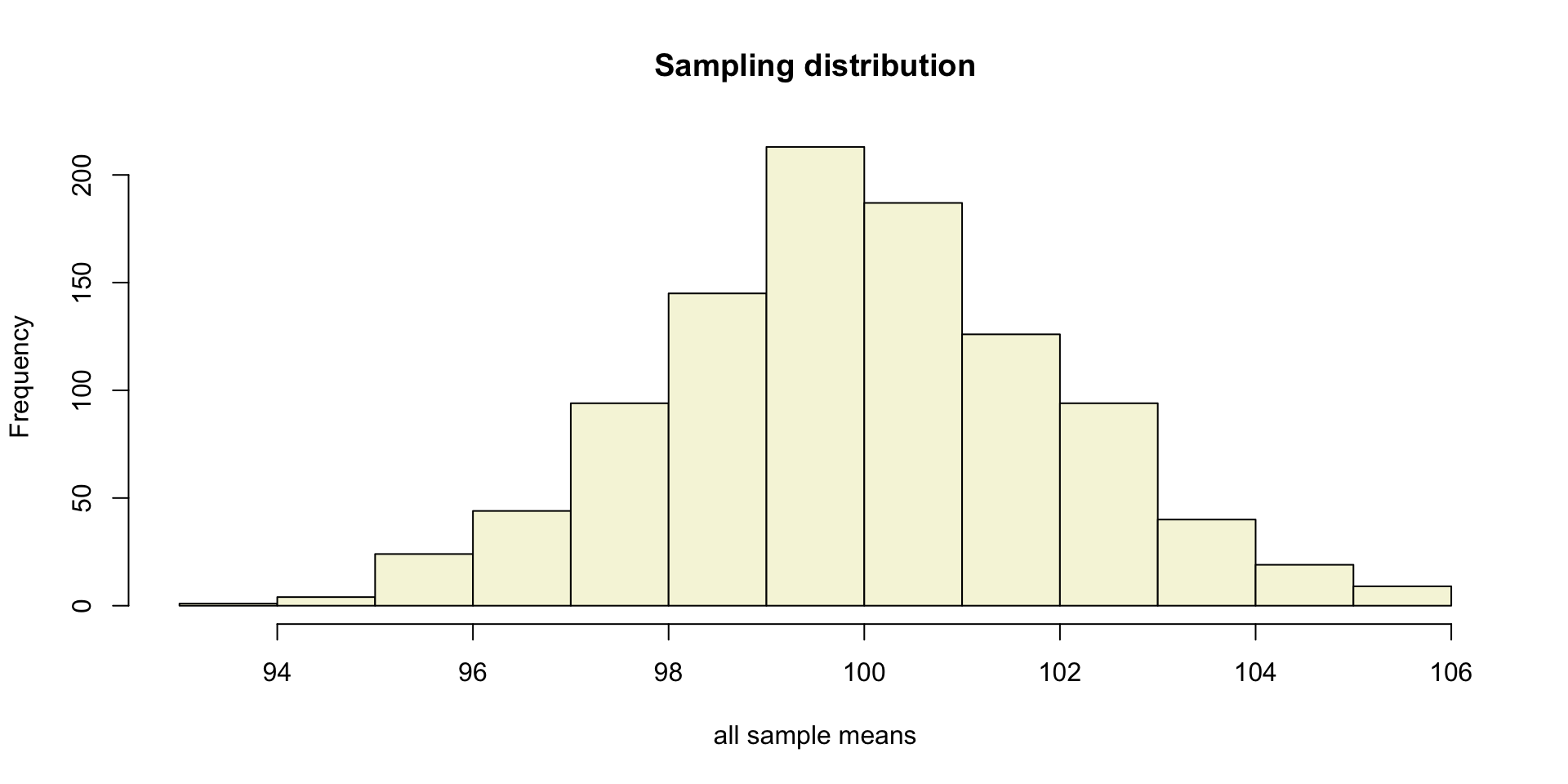
More samples
let’s take more samples.
Mean and SE for all samples
Sampling distribution
Of the mean
Sampling distribution
T-statistic
\[T_{n-1} = \frac{\bar{x}-\mu}{SE_x} = \frac{\bar{x}-\mu}{s_x / \sqrt{n}}\]
So the t-statistic represents the deviation of the sample mean \(\bar{x}\) from the population mean \(\mu\), considering the sample size, expressed as the degrees of freedom \(df = n - 1\)
t-value
\[T_{n-1} = \frac{\bar{x}-\mu}{SE_x} = \frac{\bar{x}-\mu}{s_x / \sqrt{n}}\]
Calculate t-values
\[T_{n-1} = \frac{\bar{x}-\mu}{SE_x} = \frac{\bar{x}-\mu}{s_x / \sqrt{n}}\]
mean.x.values mu se.x.values t.values
[995,] 97.29766 100 2.288305 -1.1809370
[996,] 96.62425 100 2.014688 -1.6755693
[997,] 100.48976 100 1.989127 0.2462194
[998,] 98.88857 100 2.269812 -0.4896562
[999,] 100.47711 100 1.821491 0.2619338
[1000,] 100.44906 100 2.137183 0.2101193Sampled t-values
What is the distribution of all these t-values?
Sampled t-values
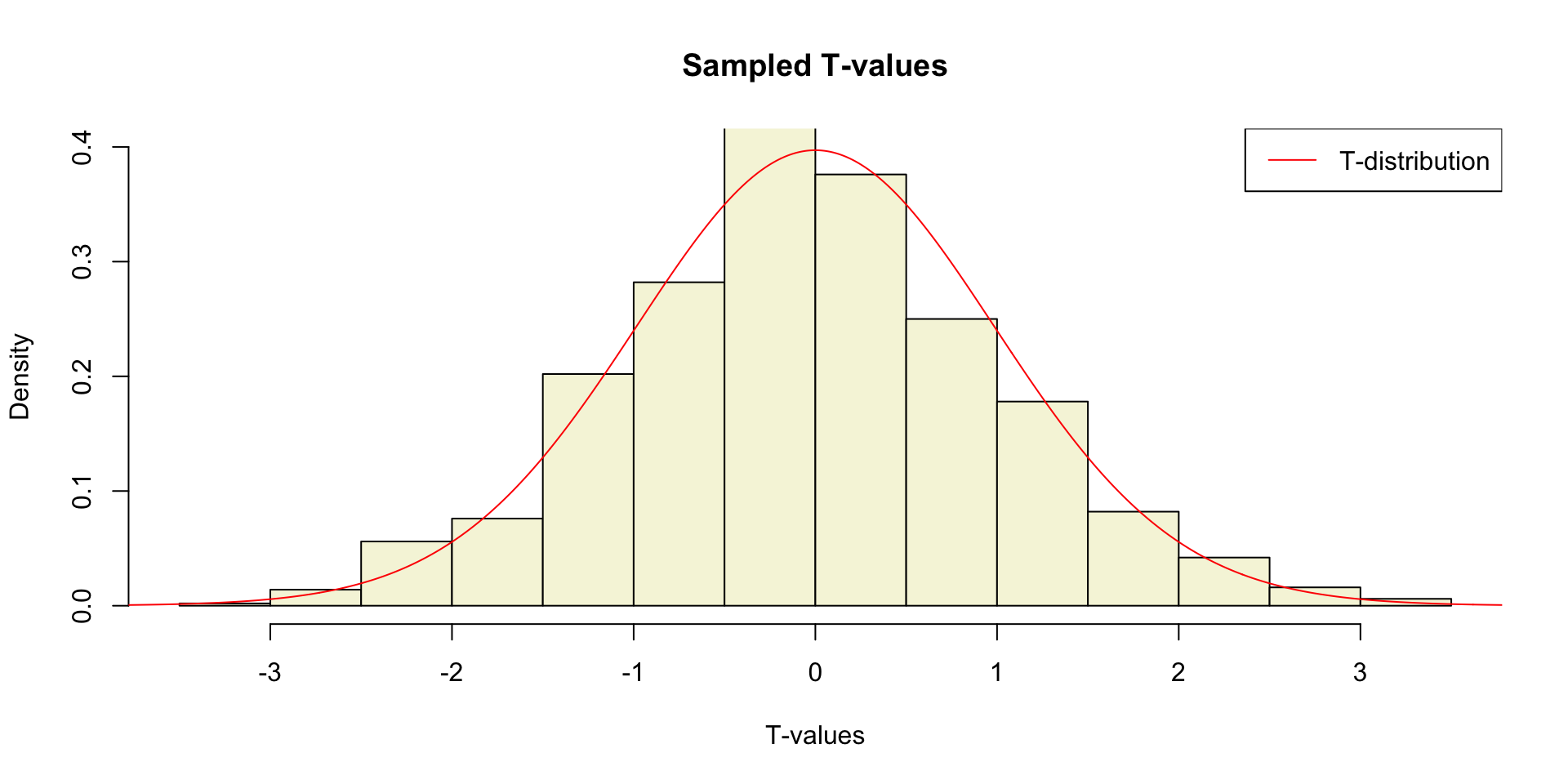
T-distribution
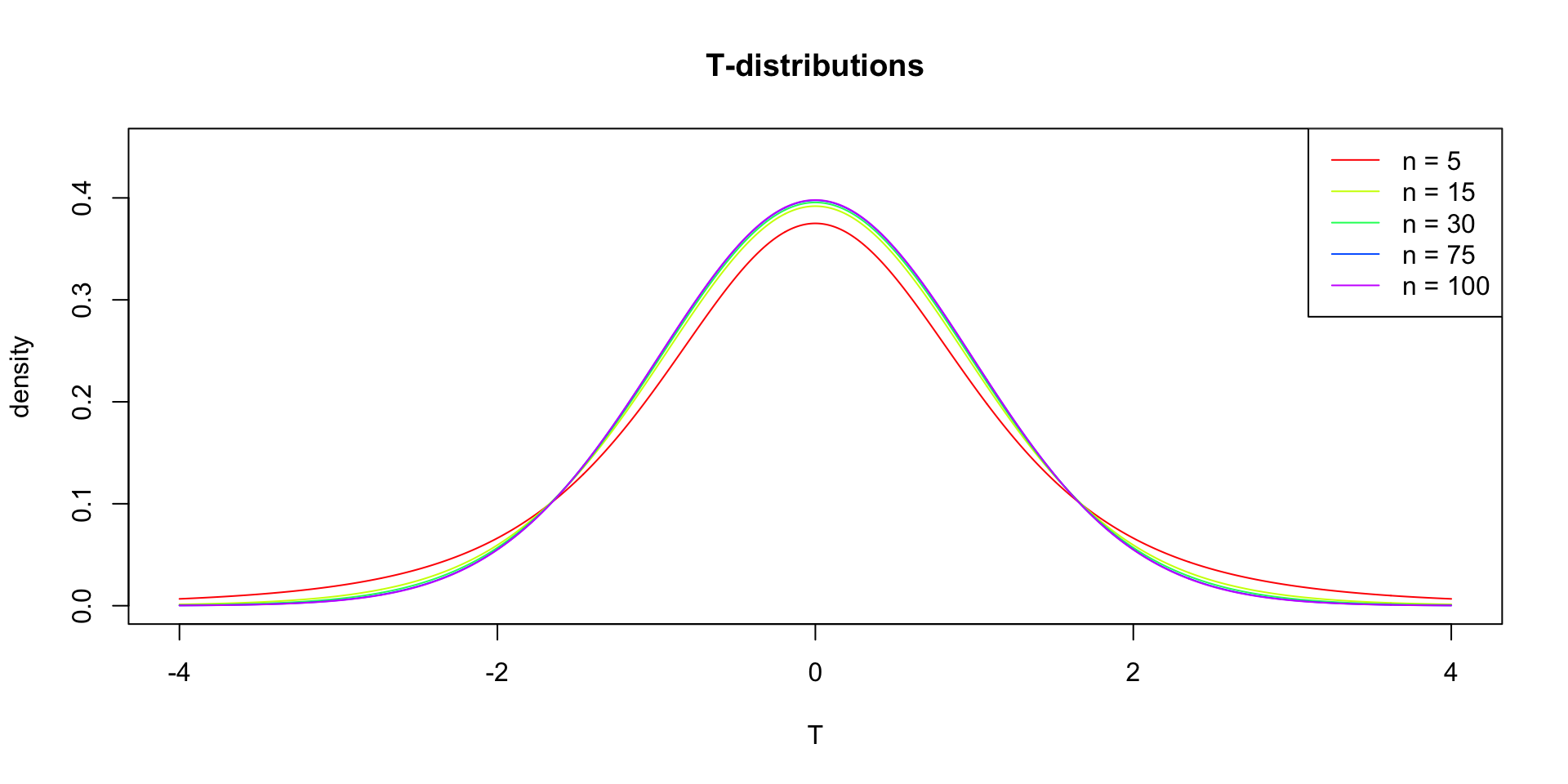
So if the population is normaly distributed (assumption of normality) the t-distribution represents the deviation of sample means from the population mean (\(\mu\)), given a certain sample size (\(df = n - 1\)).
The t-distibution therefore is different for different sample sizes and converges to a standard normal distribution if sample size is large enough.
The t-distribution is defined by:
\[\textstyle\frac{\Gamma \left(\frac{\nu+1}{2} \right)} {\sqrt{\nu\pi}\,\Gamma \left(\frac{\nu}{2} \right)} \left(1+\frac{x^2}{\nu} \right)^{-\frac{\nu+1}{2}}\!\]
where \(\nu\) is the number of degrees of freedom and \(\Gamma\) is the gamma function.
Source: wikipedia
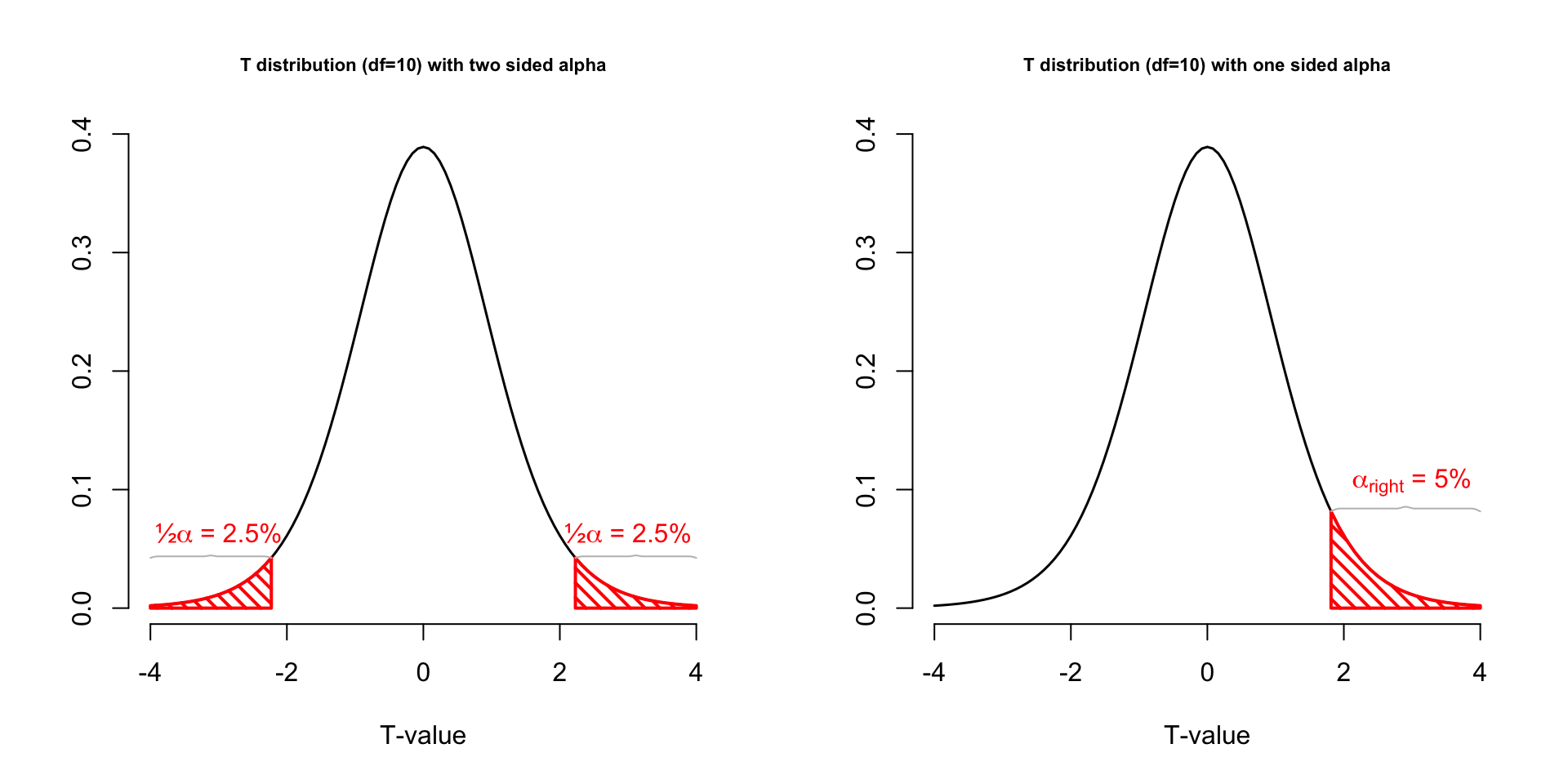
One or two sided
Two sided
- \(H_A: \bar{x} \neq \mu\)
One sided
- \(H_A: \bar{x} > \mu\)
- \(H_A: \bar{x} < \mu\)
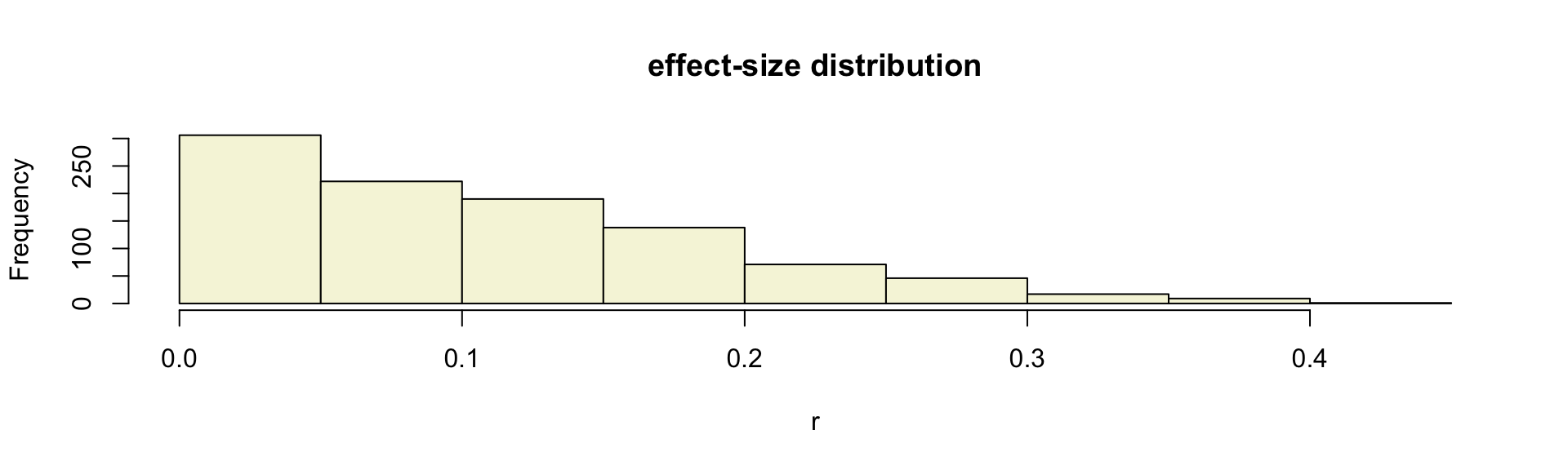
Effect-size
The effect-size is the standardised difference between the mean and the expected \(\mu\). In the t-test effect-size is expressed as \(r\).
\[r = \sqrt{\frac{t^2}{t^2 + \text{df}}}\]
Effect-sizes
We can also calculate effect-sizes for all our calculated t-values. Under the assumption of \(H_0\) the effect-size distribution looks like this.
mean.x.values mu se.x.values t.values r
[995,] 97.29766 100 2.288305 -1.1809370 0.15725626
[996,] 96.62425 100 2.014688 -1.6755693 0.22037898
[997,] 100.48976 100 1.989127 0.2462194 0.03318193
[998,] 98.88857 100 2.269812 -0.4896562 0.06588179
[999,] 100.47711 100 1.821491 0.2619338 0.03529714
[1000,] 100.44906 100 2.137183 0.2101193 0.02832112Effect-size distribution
Cohen (1988)
- Small: \(0 \leq .1\)
- Medium: \(.1 \leq .3\)
- Large: \(.3 \leq .5\)
Power
- Strive for 80%
- Based on know effect size
- Calculate number of subjects needed
- Use G*Power to calculate
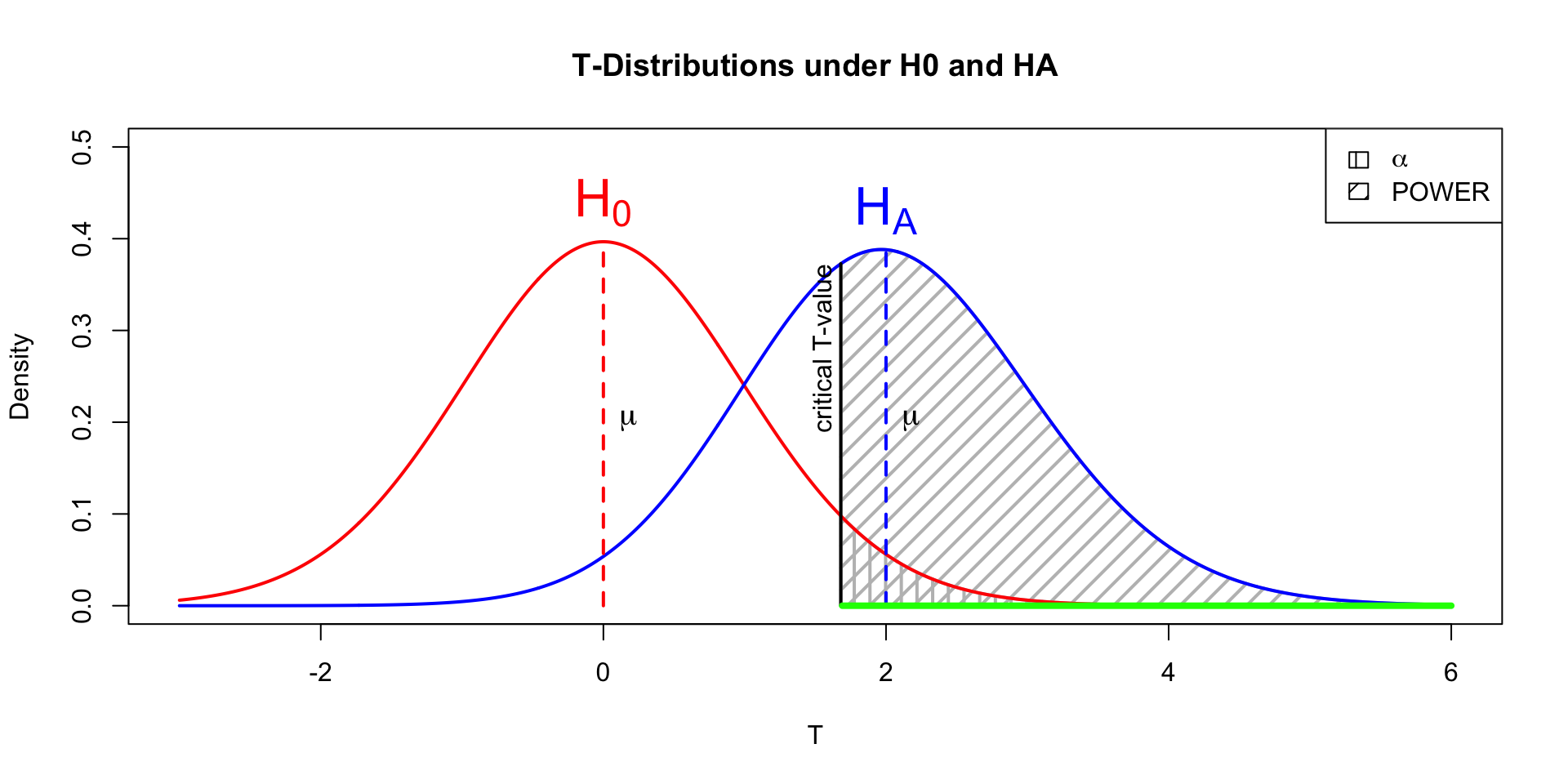
Alpha Power
T = seq(-3,6,.01)
N = 45
E = 2
# Set plot
plot(0,0,
type = "n",
ylab = "Density",
xlab = "T",
ylim = c(0,.5),
xlim = c(-3,6),
main = "T-Distributions under H0 and HA")
critical_t = qt(.05,N-1,lower.tail=FALSE)
# Alpha
range_x = seq(critical_t,6,.01)
polygon(c(range_x,rev(range_x)),
c(range_x*0,rev(dt(range_x,N-1,ncp=0))),
col = "grey",
density = 10,
angle = 90,
lwd = 2)
# Power
range_x = seq(critical_t,6,.01)
polygon(c(range_x,rev(range_x)),
c(range_x*0,rev(dt(range_x,N-1,ncp=E))),
col = "grey",
density = 10,
angle = 45,
lwd = 2)
lines(T,dt(T,N-1,ncp=0),col="red", lwd=2) # H0 line
lines(T,dt(T,N-1,ncp=E),col="blue",lwd=2) # HA line
# Critical value
lines(rep(critical_t,2),c(0,dt(critical_t,N-1,ncp=E)),lwd=2,col="black")
text(critical_t,dt(critical_t,N-1,ncp=E),"critical T-value",pos=2, srt = 90)
# H0 and HA
text(0,dt(0,N-1,ncp=0),expression(H[0]),pos=3,col="red", cex=2)
text(E,dt(E,N-1,ncp=E),expression(H[A]),pos=3,col="blue",cex=2)
# Mu H0 line
lines(c(0,0),c(0,dt(0,N-1)), col="red", lwd=2,lty=2)
text(0,dt(0,N-1,ncp=0)/2,expression(mu),pos=4,cex=1.2)
# Mu HA line
lines(c(E,E),c(0,dt(E,N-1,ncp=E)),col="blue",lwd=2,lty=2)
text(E,dt(0,N-1,ncp=0)/2,expression(paste(mu)),pos=4,cex=1.2)
# t-value
lines( c(critical_t+.01,6),c(0,0),col="green",lwd=4)
# Legend
legend("topright", c(expression(alpha),'POWER'),density=c(10,10),angle=c(90,45))Alpha Power
Multiple regression
Multiple regression
\[\LARGE{\text{outcome} = \text{model} + \text{error}}\]
In statistics, linear regression is a linear approach for modeling the relationship between a scalar dependent variable y and one or more explanatory variables denoted X.
\[\LARGE{Y_i = \beta_0 + \beta_1 X_{1i} + \beta_2 X_{2i} + \dotso + \beta_n X_{ni} + \epsilon_i}\]
In linear regression, the relationships are modeled using linear predictor functions whose unknown model parameters \(\beta\)’s are estimated from the data.
Source: wikipedia
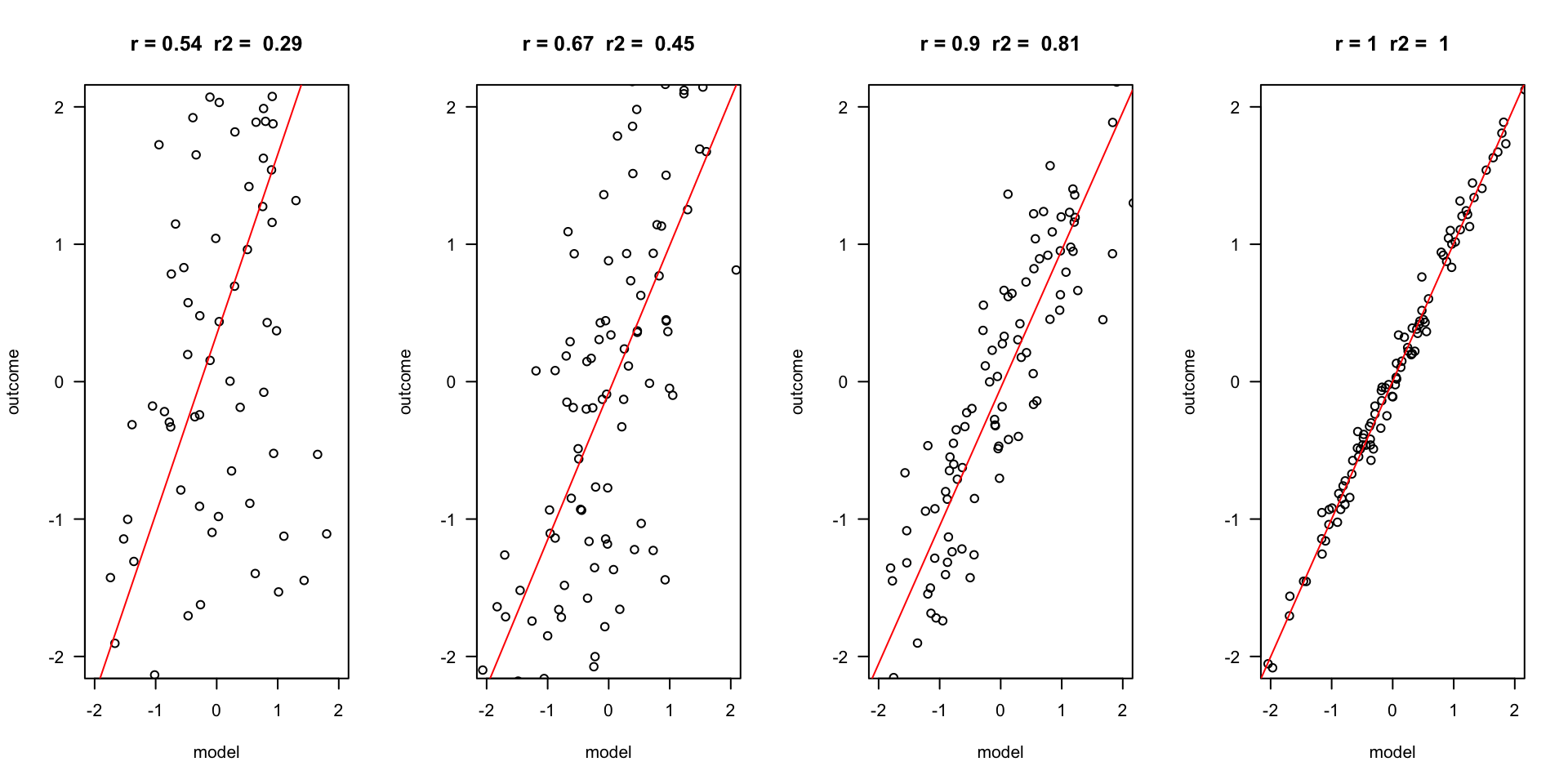
Outcome vs Model
error = c(2, 1, .5, .1)
n = 100
layout(matrix(1:4,1,4))
for(e in error) {
x = rnorm(n)
y = x + rnorm(n, 0 , e)
r = round(cor(x,y), 2)
r.2 = round(r^2, 2)
plot(x,y, las = 1, ylab = "outcome", xlab = "model", main = paste("r =", r," r2 = ", r.2), ylim=c(-2,2), xlim=c(-2,2))
fit <- lm(y ~ x)
abline(fit, col = "red")
}Outcome vs Model
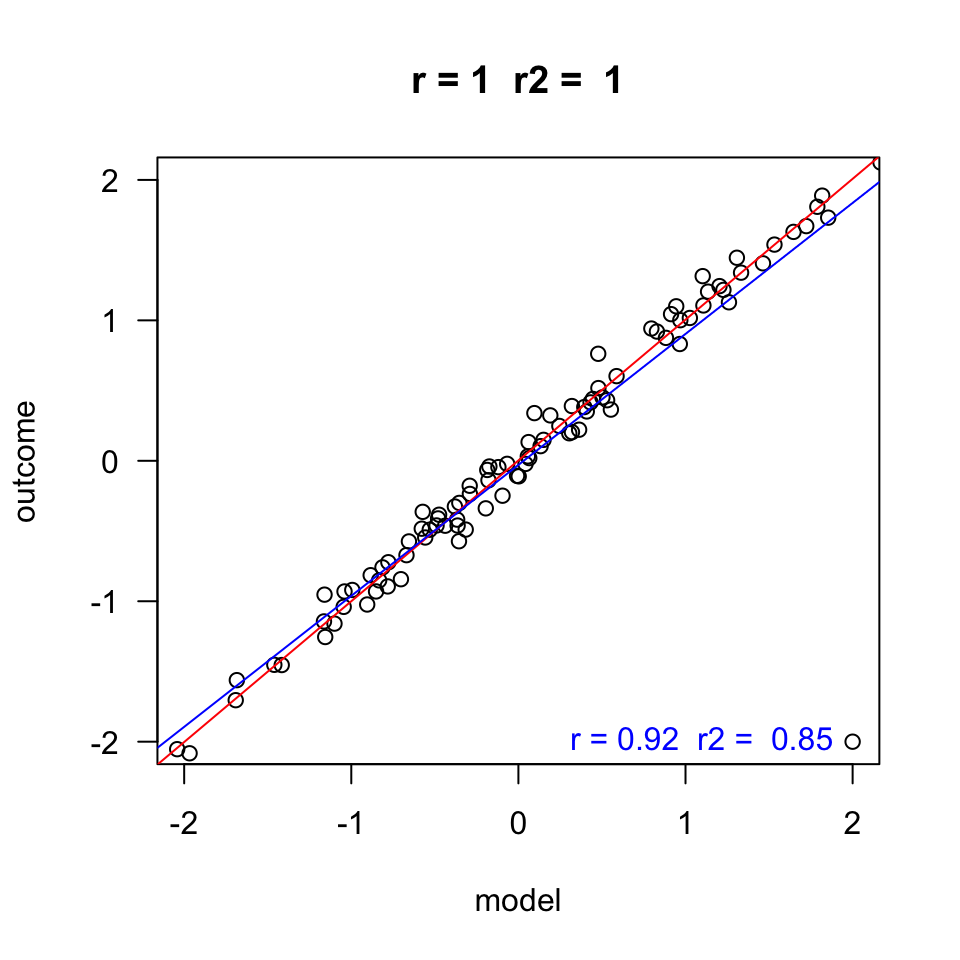
Assumptions
A selection from Field (8.3.2.1. Assumptions of the linear model):
For simple regression
- Sensitivity
- Homoscedasticity
Plus multiple regressin
- Multicollinearity
- Linearity
Sensitivity
Outliers
- Extreme residuals
- Cook’s distance (< 1)
- Mahalonobis (< 11 at N = 30)
- Laverage (The average leverage value is defined as (k + 1)/n)
Homoscedasticity
- Variance of residual should be equal across all expected values
- Look at scatterplot of standardized: expected values \(\times\) residuals. Roughly round shape is needed.
Code
set.seed(27364)
fit <- lm(x[2:n] ~ y[2:n])
ZPRED = scale(fit$fitted.values)
ZREDID = scale(fit$residuals)
plot(ZPRED, ZREDID)
abline(h = 0, v = 0, lwd=2)
#install.packages("plotrix")
if(!"plotrix" %in% installed.packages()) { install.packages("plotrix") };
library("plotrix")
draw.circle(0,0,1.7,col=rgb(1,0,0,.5))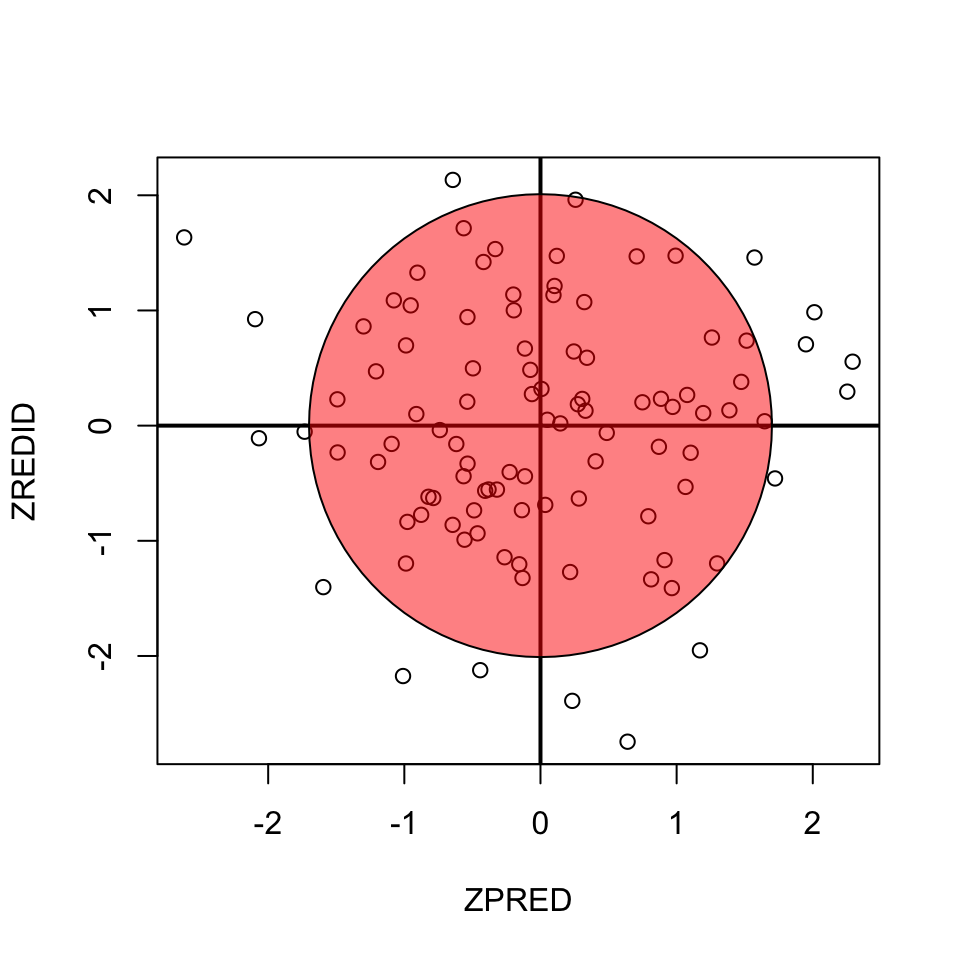
Multicollinearity
To adhere to the multicollinearity assumptien, there must not be a too high linear relation between the predictor variables.
This can be assessed through:
- Correlations
- Matrix scatterplot
- Tolerance > 0.2

Linearity
For the linearity assumption to hold, the predictors must have a linear relation to the outcome variable.
This can be checked through:
- Correlations
- Matrix scatterplot with predictors and outcome variable
Example
Perdict study outcome based on IQ and motivation.
Read data
# data <- read.csv('IQ.csv', header=T)
data <- read.csv('http://shklinkenberg.github.io/statistics-lectures/topics/regression_multiple_predictors/IQ.csv', header=TRUE)
head(data) Studieprestatie Motivatie IQ
1 2.710330 3.276778 129.9922
2 2.922617 2.598901 128.4936
3 1.997056 3.207279 130.2709
4 2.322539 2.104968 125.7457
5 2.162133 3.264948 128.6770
6 2.278899 2.217771 127.5349Regression model in R
Perdict study outcome based on IQ and motivation.
What is the model
(Intercept) IQ motivation
-30.2822189 0.2690984 -0.6314253 De beta coëfficients are:
- \(b_0\) (intercept) = -30.28
- \(b_1\) = 0.27
- \(b_2\) = -0.63.
Model summaries
Call:
lm(formula = study.outcome ~ IQ + motivation)
Residuals:
Min 1Q Median 3Q Max
-0.75127 -0.17437 0.00805 0.17230 0.44435
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -30.28222 6.64432 -4.558 5.76e-05 ***
IQ 0.26910 0.05656 4.758 3.14e-05 ***
motivation -0.63143 0.23143 -2.728 0.00978 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.2714 on 36 degrees of freedom
Multiple R-squared: 0.7528, Adjusted R-squared: 0.739
F-statistic: 54.8 on 2 and 36 DF, p-value: 1.192e-11Visual
What are the expected values based on this model
\[\widehat{\text{studie prestatie}} = b_0 + b_1 \text{IQ} + b_2 \text{motivation}\]
\[\text{model} = \widehat{\text{studie prestatie}}\]
Apply regression model
\[\widehat{\text{studie prestatie}} = b_0 + b_1 \text{IQ} + b_2 \text{motivation}\] \[\widehat{\text{model}} = b_0 + b_1 \text{IQ} + b_2 \text{motivation}\]
model b.0 b.1 IQ b.2 motivation
[1,] 2.753512 -30.28 0.27 129.9922 -0.63 3.276778
[2,] 2.775969 -30.28 0.27 128.4936 -0.63 2.598901
[3,] 2.872561 -30.28 0.27 130.2709 -0.63 3.207279
[4,] 2.345205 -30.28 0.27 125.7457 -0.63 2.104968
[5,] 2.405860 -30.28 0.27 128.6770 -0.63 3.264948\[\widehat{\text{model}} = -30.28 + 0.27 \times \text{IQ} + -0.63 \times \text{motivation}\]
How far are we off?
Outcome = Model + Error
Is that true?
[1] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
[16] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
[31] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE- Yes!
Visual
plot(study.outcome, xlab='personen', ylab='study.outcome')
n = length(study.outcome)
gemiddelde.study.outcome = mean(study.outcome)
## Voeg het gemiddelde toe
lines(c(1, n), rep(gemiddelde.study.outcome, 2))
## Wat is de totale variantie?
segments(1:n, study.outcome, 1:n, gemiddelde.study.outcome, col='blue')
## Wat zijn onze verwachte scores op basis van dit regressie model?
points(model, col='orange')
## Hoever zitten we ernaast, wat is de error?
segments(1:n, study.outcome, 1:n, model, col='purple', lwd=3)Visual
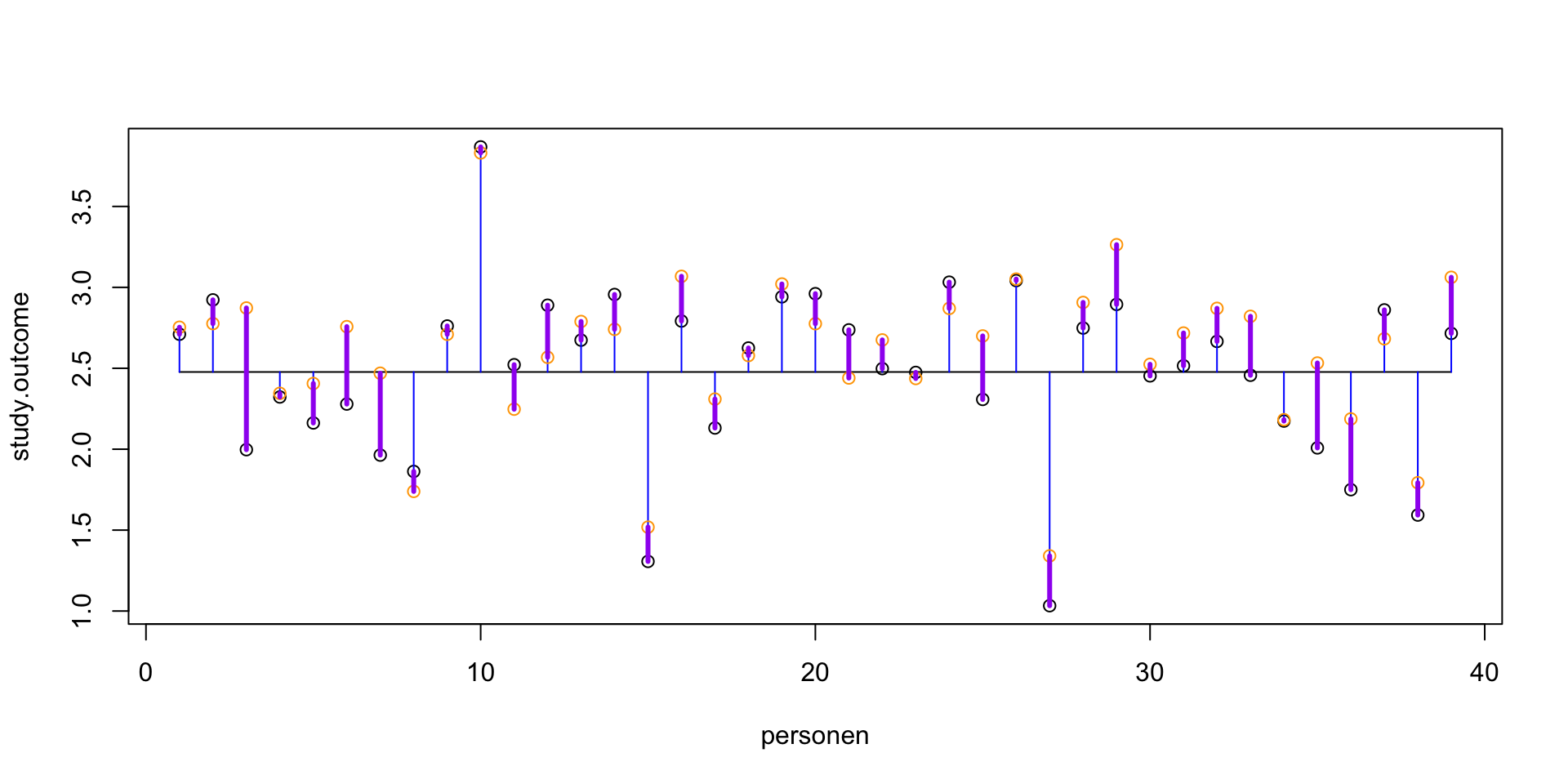
Explained variance
The explained variance is the deviation of the estimated model outcome compared to the total mean.
To get a percentage of explained variance, it must be compared to the total variance. In terms of squares:
\[\frac{{SS}_{model}}{{SS}_{total}}\]
We also call this: \(r^2\) of \(R^2\).
Compare models
fit1 <- lm(study.outcome ~ motivation, data)
fit2 <- lm(study.outcome ~ motivation + IQ, data)
# summary(fit1)
# summary(fit2)
anova(fit1, fit2)Analysis of Variance Table
Model 1: study.outcome ~ motivation
Model 2: study.outcome ~ motivation + IQ
Res.Df RSS Df Sum of Sq F Pr(>F)
1 37 4.3191
2 36 2.6518 1 1.6673 22.635 3.144e-05 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1End
Contact

Wetenschapsfilosofie & Statistisch Redeneren
