T-distribution &
Multiple regression

Klinkenberg

University of Amsterdam

20 sep 2022

T-distribution

Gosset

In probability and statistics, Student’s t-distribution (or simply the t-distribution) is any member of a family of continuous probability distributions that arises when estimating the mean of a normally distributed population in situations where the sample size is small and population standard deviation is unknown.

In the English-language literature it takes its name from William Sealy Gosset’s 1908 paper in Biometrika under the pseudonym “Student”. Gosset worked at the Guinness Brewery in Dublin, Ireland, and was interested in the problems of small samples, for example the chemical properties of barley where sample sizes might be as low as 3.

Source: Wikipedia

Population distribution

layout(matrix(c(2:6,1,1,7:8,1,1,9:13), 4, 4))

n  = 56    # Sample size
df = n - 1 # Degrees of freedom

mu    = 100
sigma = 15

IQ = seq(mu-45, mu+45, 1)

par(mar=c(4,2,2,0))  
plot(IQ, dnorm(IQ, mean = mu, sd = sigma), type='l', col="red", main = "Population Distribution")

n.samples = 12

for(i in 1:n.samples) {
  
  par(mar=c(2,2,2,0))  
  hist(rnorm(n, mu, sigma), main="Sample Distribution", cex.axis=.5, col="beige", cex.main = .75)
  
}

Population distribution

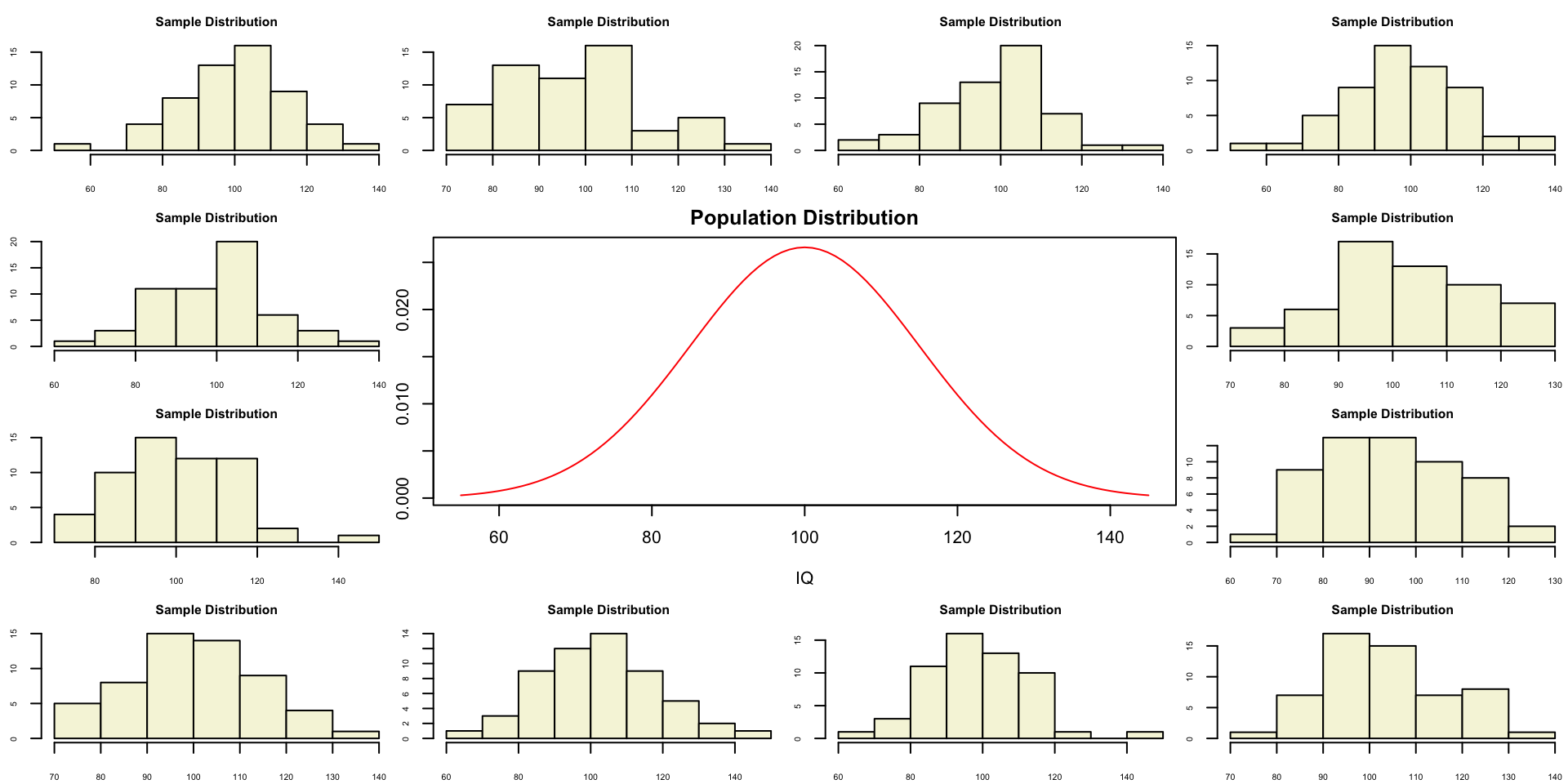
A sample

Let’s take one sample from our normal populatiion and calculate the t-value.

x = rnorm(n, mu, sigma); x

 [1] 105.97091  97.88795  96.59252 101.97494 114.81159 123.34823 105.39531
 [8]  86.35303  84.49523  80.42120  86.31988 118.64665 100.35848 137.86111
[15] 114.91078  80.79485  90.37722 136.44031 123.64622  99.29570 134.74928
[22] 108.68651  96.77961 107.46039 105.73403 100.95100  86.91514  75.50513
[29] 109.02407  84.63182 114.97081  92.17397 115.11011 114.97649 105.30372
[36]  95.37380  71.99298 109.96248 112.74284  70.13382  72.16366  95.65371
[43] 109.27013  83.50502 113.53344  93.60204  98.88010 114.53777  97.82642
[50]  93.81316  99.32199  85.80533 118.89700  83.79097  96.21963 119.69839

hist(x, main = "Sample distribution", col = "beige", breaks = 15)
text(80, 10, round(mean(x),2))

A sample

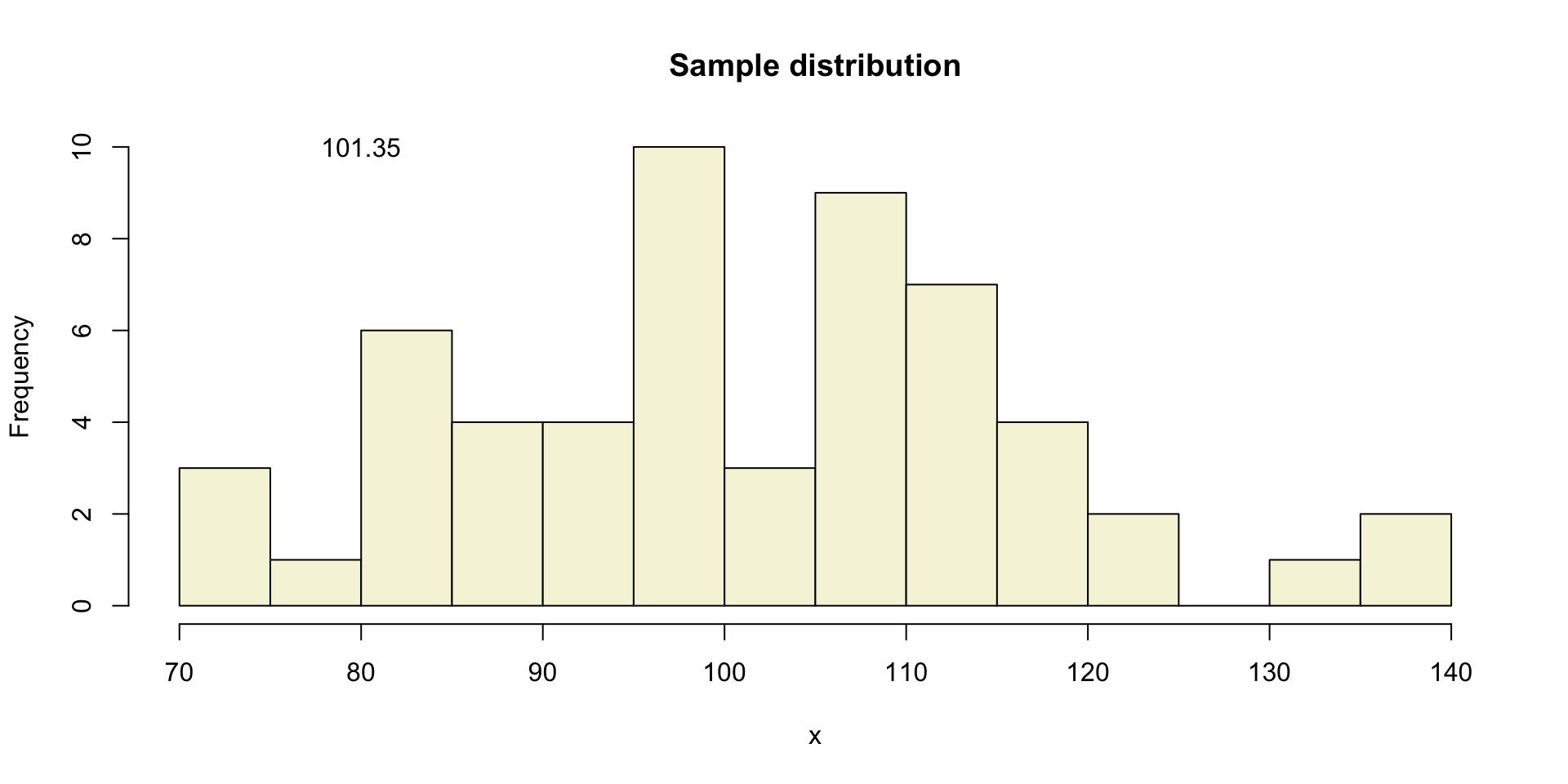
More samples

let’s take more samples.

n.samples     = 1000
mean.x.values = vector()
se.x.values   = vector()

for(i in 1:n.samples) {
  x = rnorm(n, mu, sigma)
  mean.x.values[i] = mean(x)
  se.x.values[i]   = (sd(x) / sqrt(n))
}

Mean and SE for all samples

head(cbind(mean.x.values, se.x.values))

     mean.x.values se.x.values
[1,]     102.28217    2.046748
[2,]     102.16009    1.959304
[3,]     101.43661    1.900249
[4,]      98.77351    2.073932
[5,]      96.24067    2.239351
[6,]      97.94926    2.125018

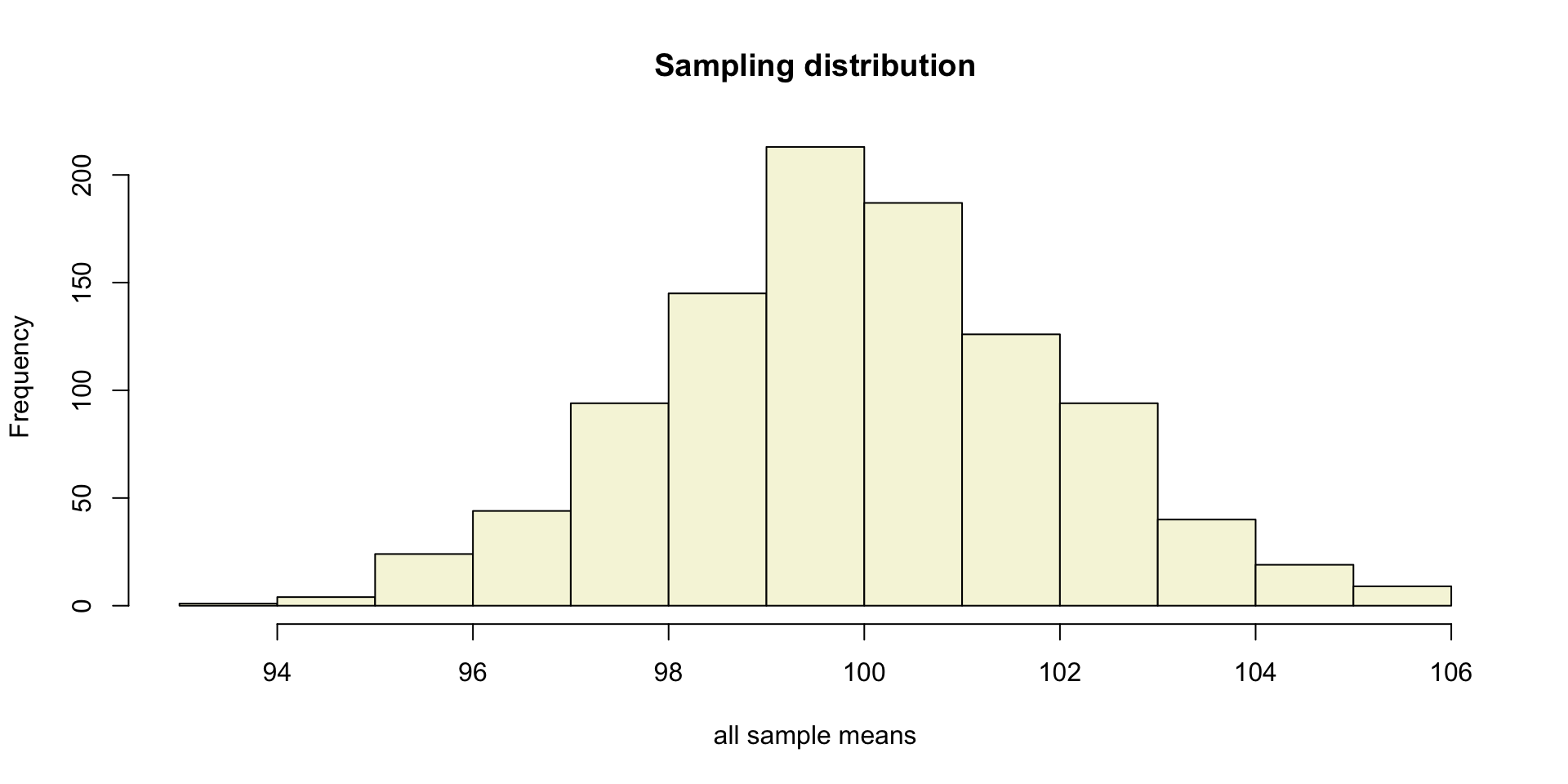
Sampling distribution

Of the mean

hist(mean.x.values, 
     col  = "beige", 
     main = "Sampling distribution", 
     xlab = "all sample means")

Sampling distribution

T-statistic

\[T_{n-1} = \frac{\bar{x}-\mu}{SE_x} = \frac{\bar{x}-\mu}{s_x / \sqrt{n}}\]

So the t-statistic represents the deviation of the sample mean \(\bar{x}\) from the population mean \(\mu\), considering the sample size, expressed as the degrees of freedom \(df = n - 1\)

t-value

\[T_{n-1} = \frac{\bar{x}-\mu}{SE_x} = \frac{\bar{x}-\mu}{s_x / \sqrt{n}}\]

t = (mean(x) - mu) / (sd(x) / sqrt(n))
t

[1] 0.2101193

Calculate t-values

\[T_{n-1} = \frac{\bar{x}-\mu}{SE_x} = \frac{\bar{x}-\mu}{s_x / \sqrt{n}}\]

t.values = (mean.x.values - mu) / se.x.values

tail(cbind(mean.x.values, mu, se.x.values, t.values))

        mean.x.values  mu se.x.values   t.values
 [995,]      97.29766 100    2.288305 -1.1809370
 [996,]      96.62425 100    2.014688 -1.6755693
 [997,]     100.48976 100    1.989127  0.2462194
 [998,]      98.88857 100    2.269812 -0.4896562
 [999,]     100.47711 100    1.821491  0.2619338
[1000,]     100.44906 100    2.137183  0.2101193

Sampled t-values

What is the distribution of all these t-values?

hist(t.values, 
     freq = F, 
     main = "Sampled T-values", 
     xlab = "T-values",
     col  = "beige",
     ylim = c(0, .4))
T = seq(-4, 4, .01)
lines(T, dt(T,df), col = "red")
legend("topright", lty = 1, col="red", legend = "T-distribution")

Sampled t-values

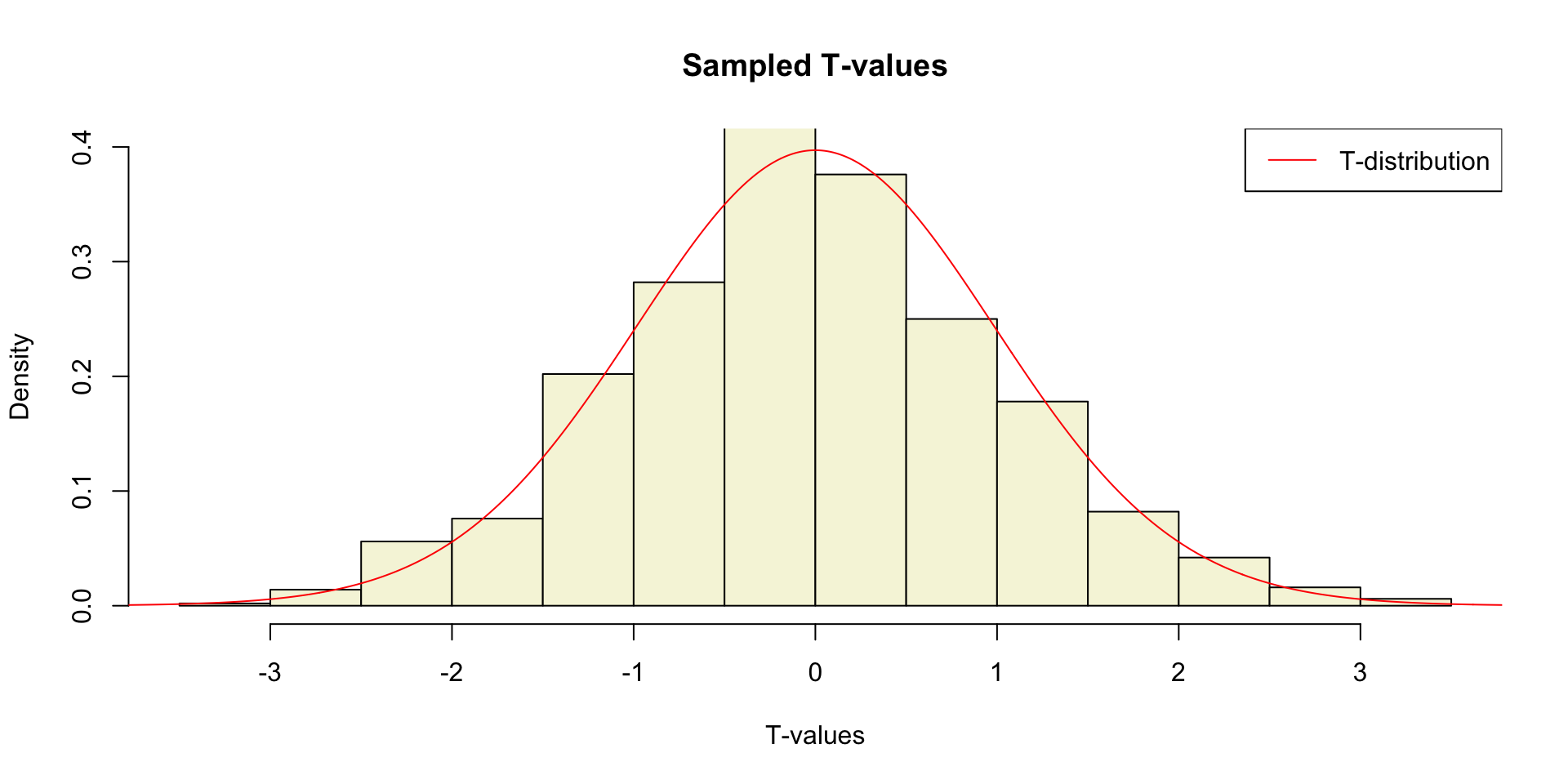
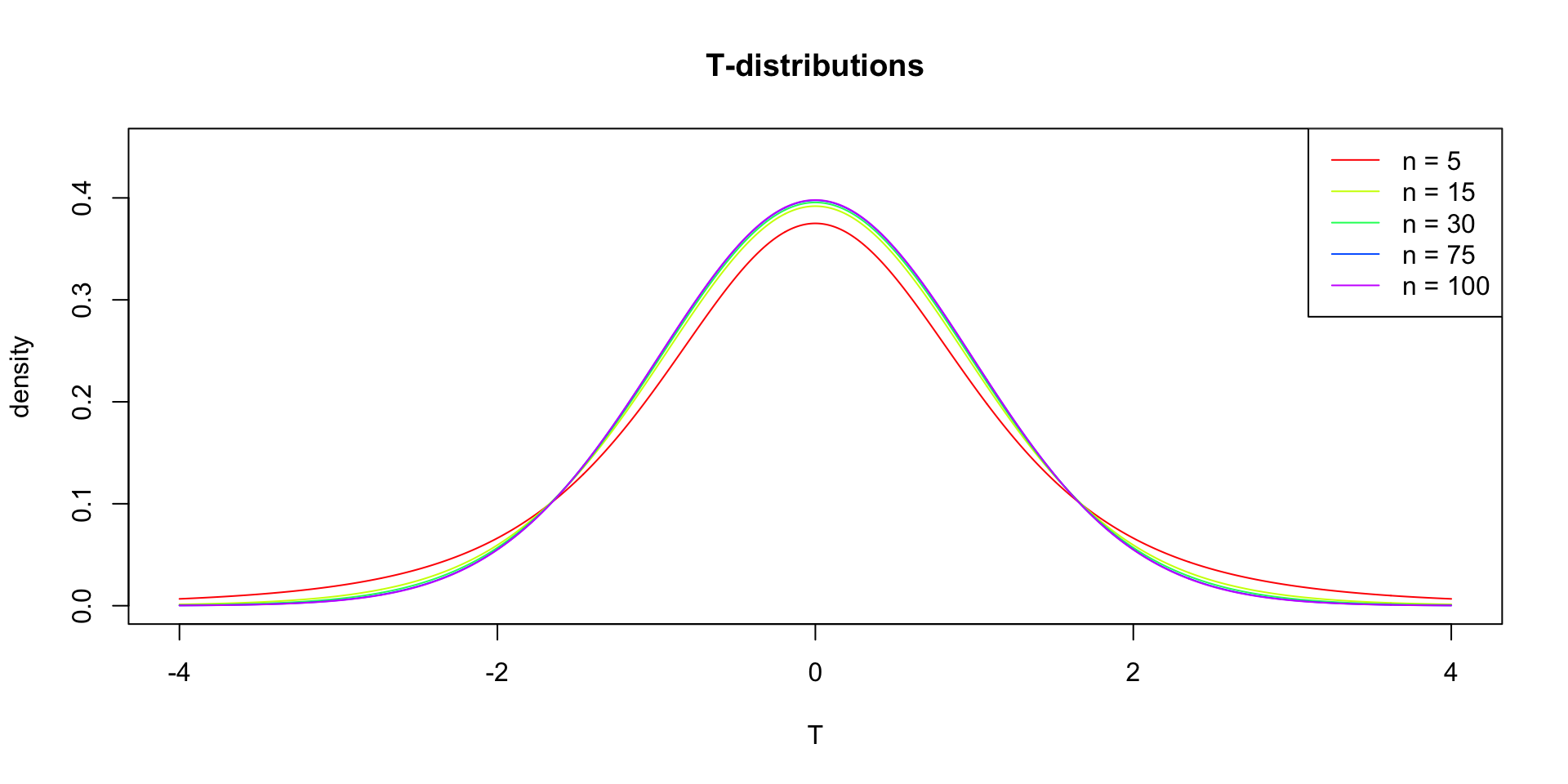
T-distribution

So if the population is normaly distributed (assumption of normality) the t-distribution represents the deviation of sample means from the population mean (\(\mu\)), given a certain sample size (\(df = n - 1\)).

The t-distibution therefore is different for different sample sizes and converges to a standard normal distribution if sample size is large enough.

The t-distribution is defined by:

\[\textstyle\frac{\Gamma \left(\frac{\nu+1}{2} \right)} {\sqrt{\nu\pi}\,\Gamma \left(\frac{\nu}{2} \right)} \left(1+\frac{x^2}{\nu} \right)^{-\frac{\nu+1}{2}}\!\]

where \(\nu\) is the number of degrees of freedom and \(\Gamma\) is the gamma function.

Source: wikipedia

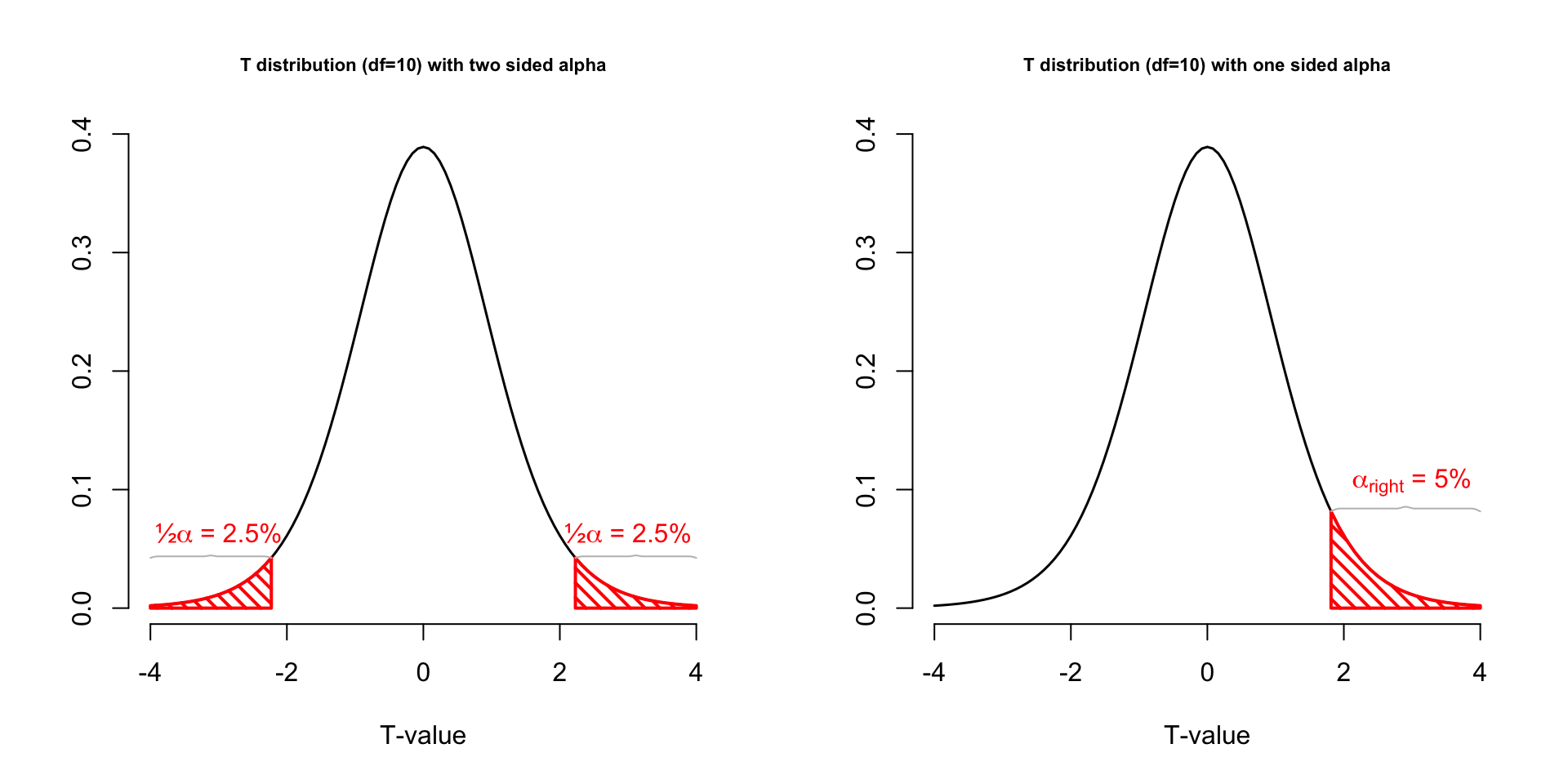
One or two sided

Two sided

\(H_A: \bar{x} \neq \mu\)

One sided

\(H_A: \bar{x} > \mu\)
\(H_A: \bar{x} < \mu\)

Effect-size

The effect-size is the standardised difference between the mean and the expected \(\mu\). In the t-test effect-size is expressed as \(r\).

\[r = \sqrt{\frac{t^2}{t^2 + \text{df}}}\]

r = sqrt(t^2/(t^2 + df))

r

[1] 0.2603778

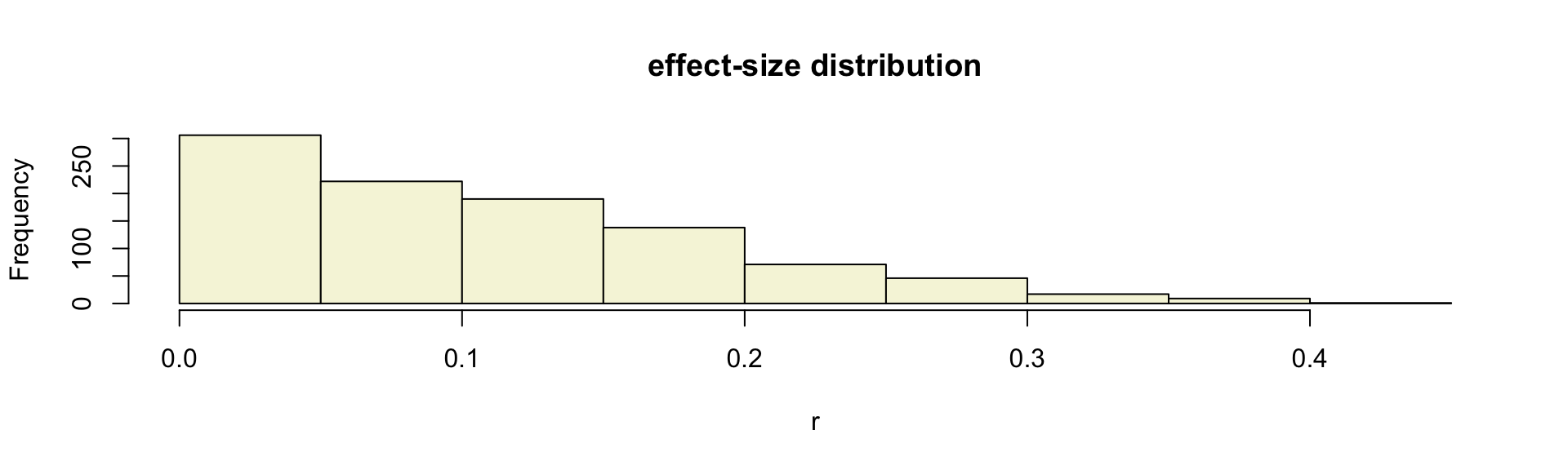
Effect-sizes

We can also calculate effect-sizes for all our calculated t-values. Under the assumption of \(H_0\) the effect-size distribution looks like this.

        mean.x.values  mu se.x.values   t.values          r
 [995,]      97.29766 100    2.288305 -1.1809370 0.15725626
 [996,]      96.62425 100    2.014688 -1.6755693 0.22037898
 [997,]     100.48976 100    1.989127  0.2462194 0.03318193
 [998,]      98.88857 100    2.269812 -0.4896562 0.06588179
 [999,]     100.47711 100    1.821491  0.2619338 0.03529714
[1000,]     100.44906 100    2.137183  0.2101193 0.02832112

Effect-size distribution

Cohen (1988)

Small: \(0 \leq .1\)
Medium: \(.1 \leq .3\)
Large: \(.3 \leq .5\)

Power

Strive for 80%
Based on know effect size
Calculate number of subjects needed
Use G*Power to calculate

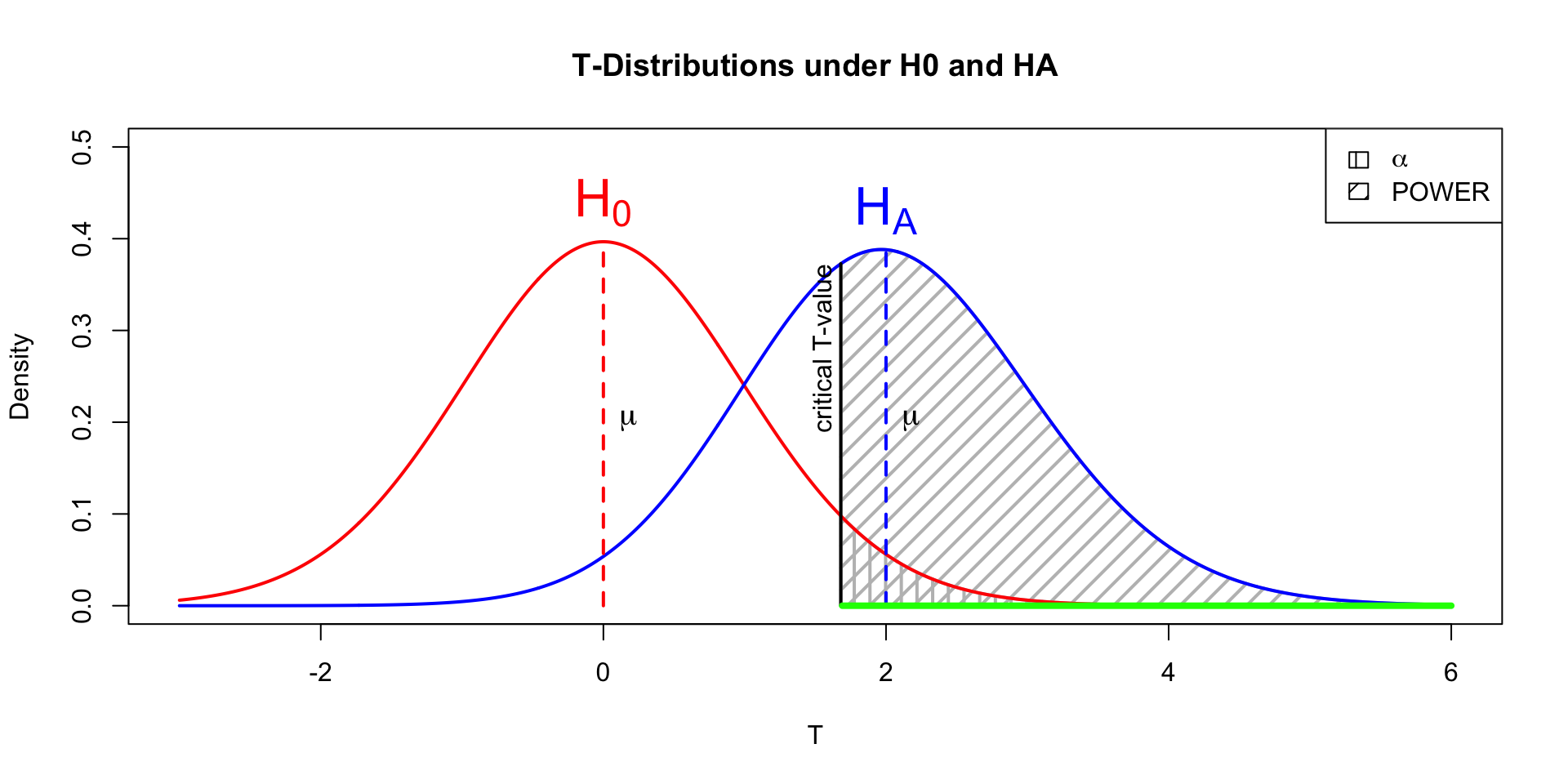
Alpha Power

T = seq(-3,6,.01)
N = 45
E = 2

# Set plot
plot(0,0,
     type = "n",
     ylab = "Density",
     xlab = "T",
     ylim = c(0,.5),
     xlim = c(-3,6),
     main = "T-Distributions under H0 and HA")

critical_t = qt(.05,N-1,lower.tail=FALSE)

# Alpha
range_x = seq(critical_t,6,.01)
polygon(c(range_x,rev(range_x)),
        c(range_x*0,rev(dt(range_x,N-1,ncp=0))),
        col     = "grey",
        density = 10,
        angle   = 90,
        lwd     = 2)

# Power
range_x = seq(critical_t,6,.01)
polygon(c(range_x,rev(range_x)),
        c(range_x*0,rev(dt(range_x,N-1,ncp=E))),
        col     = "grey",
        density = 10,
        angle   = 45,
        lwd     = 2)

lines(T,dt(T,N-1,ncp=0),col="red", lwd=2) # H0 line
lines(T,dt(T,N-1,ncp=E),col="blue",lwd=2) # HA line

# Critical value
lines(rep(critical_t,2),c(0,dt(critical_t,N-1,ncp=E)),lwd=2,col="black")
text(critical_t,dt(critical_t,N-1,ncp=E),"critical T-value",pos=2, srt = 90)

# H0 and HA
text(0,dt(0,N-1,ncp=0),expression(H[0]),pos=3,col="red", cex=2)
text(E,dt(E,N-1,ncp=E),expression(H[A]),pos=3,col="blue",cex=2)

# Mu H0 line
lines(c(0,0),c(0,dt(0,N-1)), col="red",  lwd=2,lty=2)
text(0,dt(0,N-1,ncp=0)/2,expression(mu),pos=4,cex=1.2)
# Mu HA line
lines(c(E,E),c(0,dt(E,N-1,ncp=E)),col="blue",lwd=2,lty=2)
text(E,dt(0,N-1,ncp=0)/2,expression(paste(mu)),pos=4,cex=1.2)

# t-value
lines( c(critical_t+.01,6),c(0,0),col="green",lwd=4)

# Legend
legend("topright", c(expression(alpha),'POWER'),density=c(10,10),angle=c(90,45))

Alpha Power

R-Psychologist

Multiple regression

\[\LARGE{\text{outcome} = \text{model} + \text{error}}\]

In statistics, linear regression is a linear approach for modeling the relationship between a scalar dependent variable y and one or more explanatory variables denoted X.

\[\LARGE{Y_i = \beta_0 + \beta_1 X_{1i} + \beta_2 X_{2i} + \dotso + \beta_n X_{ni} + \epsilon_i}\]

In linear regression, the relationships are modeled using linear predictor functions whose unknown model parameters \(\beta\)’s are estimated from the data.

Source: wikipedia

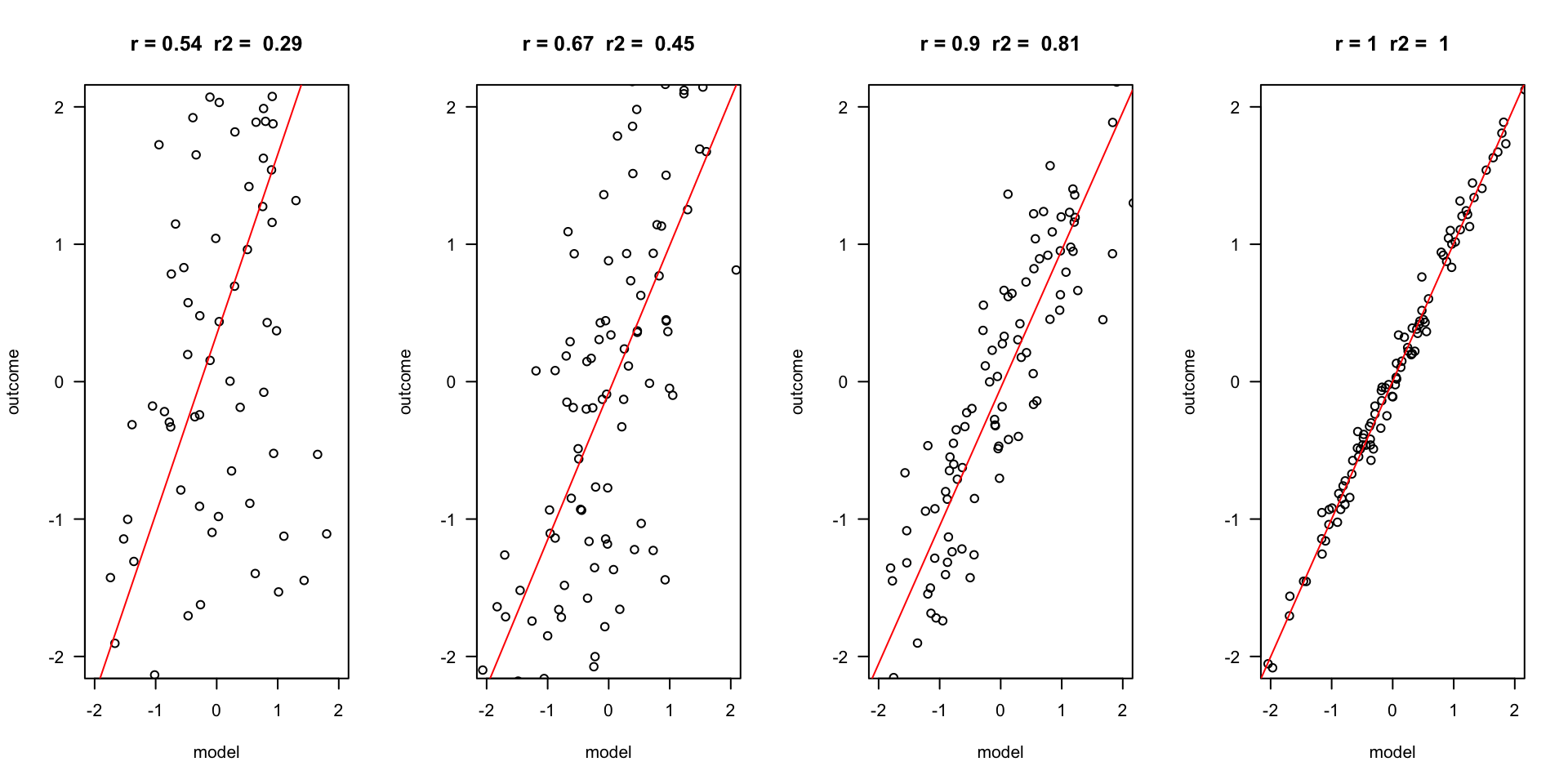
Outcome vs Model

error = c(2, 1, .5, .1)
n = 100

layout(matrix(1:4,1,4))
for(e in error) {
  
  x = rnorm(n)
  y = x + rnorm(n, 0 , e)
  
  r   = round(cor(x,y), 2)
  r.2 = round(r^2, 2)
  
  plot(x,y, las = 1, ylab = "outcome", xlab = "model", main = paste("r =", r," r2 = ", r.2), ylim=c(-2,2), xlim=c(-2,2))
  fit <- lm(y ~ x)
  abline(fit, col = "red")
  
}

Outcome vs Model

Assumptions

A selection from Field (8.3.2.1. Assumptions of the linear model):

For simple regression

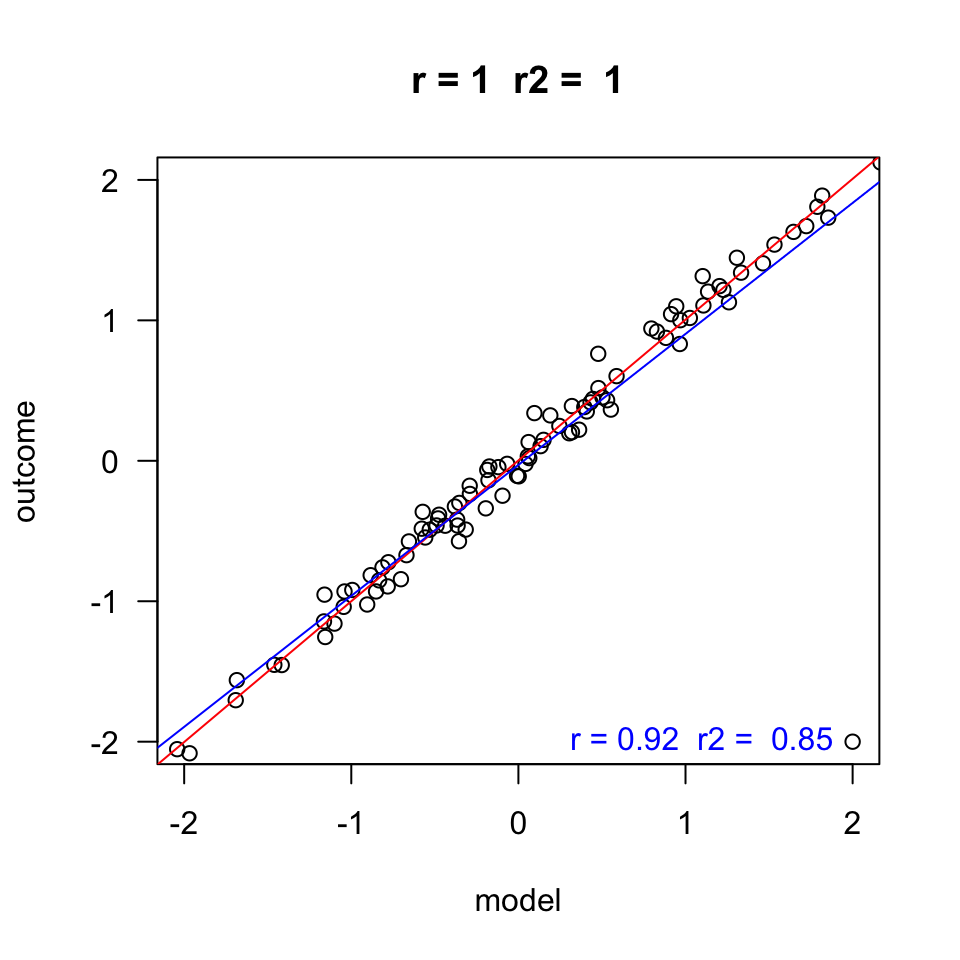
Sensitivity
Homoscedasticity

Plus multiple regressin

Multicollinearity
Linearity

Sensitivity

Outliers

Extreme residuals
- Cook’s distance (< 1)
- Mahalonobis (< 11 at N = 30)
- Laverage (The average leverage value is defined as (k + 1)/n)

Homoscedasticity

Variance of residual should be equal across all expected values
- Look at scatterplot of standardized: expected values \(\times\) residuals. Roughly round shape is needed.

Code

set.seed(27364)

fit <- lm(x[2:n] ~ y[2:n])

ZPRED  = scale(fit$fitted.values)
ZREDID = scale(fit$residuals)

plot(ZPRED, ZREDID)
abline(h = 0, v = 0, lwd=2)

#install.packages("plotrix")
if(!"plotrix" %in% installed.packages()) { install.packages("plotrix") };
library("plotrix")
draw.circle(0,0,1.7,col=rgb(1,0,0,.5))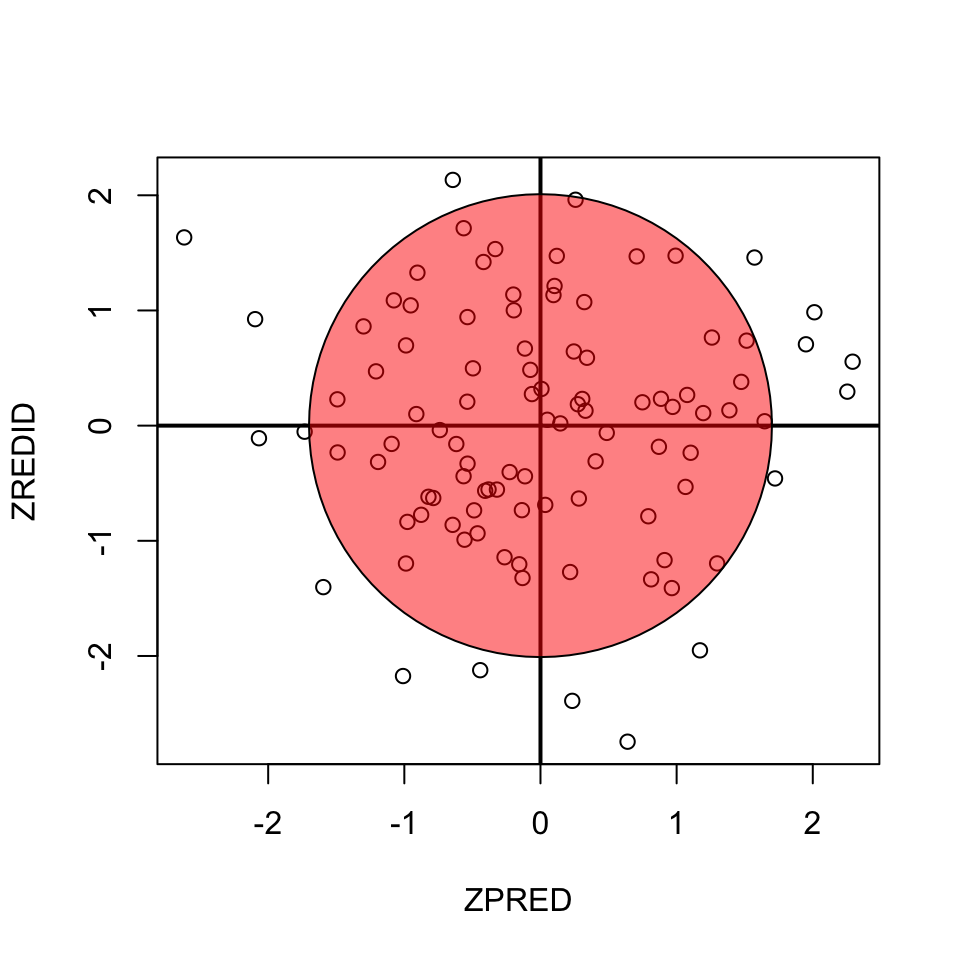

Multicollinearity

To adhere to the multicollinearity assumptien, there must not be a too high linear relation between the predictor variables.

This can be assessed through:

Correlations
Matrix scatterplot
Tolerance > 0.2

Linearity

For the linearity assumption to hold, the predictors must have a linear relation to the outcome variable.

This can be checked through:

Correlations
Matrix scatterplot with predictors and outcome variable

Example

Perdict study outcome based on IQ and motivation.

Read data

# data <- read.csv('IQ.csv', header=T)
data <- read.csv('http://shklinkenberg.github.io/statistics-lectures/topics/regression_multiple_predictors/IQ.csv', header=TRUE)

head(data)

  Studieprestatie Motivatie       IQ
1        2.710330  3.276778 129.9922
2        2.922617  2.598901 128.4936
3        1.997056  3.207279 130.2709
4        2.322539  2.104968 125.7457
5        2.162133  3.264948 128.6770
6        2.278899  2.217771 127.5349

IQ            = data$IQ
study.outcome = data$Studieprestatie
motivation    = data$Motivatie

Regression model in R

Perdict study outcome based on IQ and motivation.

fit <- lm(study.outcome ~ IQ + motivation)

What is the model

fit$coefficients

(Intercept)          IQ  motivation 
-30.2822189   0.2690984  -0.6314253

b.0 = round(fit$coefficients[1], 2) ## Intercept
b.1 = round(fit$coefficients[2], 2) ## Beta coefficient for IQ
b.2 = round(fit$coefficients[3], 2) ## Beta coefficient for motivation

De beta coëfficients are:

\(b_0\) (intercept) = -30.28
\(b_1\) = 0.27
\(b_2\) = -0.63.

Model summaries

summary(fit)


Call:
lm(formula = study.outcome ~ IQ + motivation)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.75127 -0.17437  0.00805  0.17230  0.44435 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) -30.28222    6.64432  -4.558 5.76e-05 ***
IQ            0.26910    0.05656   4.758 3.14e-05 ***
motivation   -0.63143    0.23143  -2.728  0.00978 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.2714 on 36 degrees of freedom
Multiple R-squared:  0.7528,    Adjusted R-squared:  0.739 
F-statistic:  54.8 on 2 and 36 DF,  p-value: 1.192e-11

Visual

What are the expected values based on this model

\[\widehat{\text{studie prestatie}} = b_0 + b_1 \text{IQ} + b_2 \text{motivation}\]

exp.stu.prest = b.0 + b.1 * IQ + b.2 * motivation

model = exp.stu.prest

\[\text{model} = \widehat{\text{studie prestatie}}\]

Apply regression model

\[\widehat{\text{studie prestatie}} = b_0 + b_1 \text{IQ} + b_2 \text{motivation}\] \[\widehat{\text{model}} = b_0 + b_1 \text{IQ} + b_2 \text{motivation}\]

cbind(model, b.0, b.1, IQ, b.2, motivation)[1:5,]

        model    b.0  b.1       IQ   b.2 motivation
[1,] 2.753512 -30.28 0.27 129.9922 -0.63   3.276778
[2,] 2.775969 -30.28 0.27 128.4936 -0.63   2.598901
[3,] 2.872561 -30.28 0.27 130.2709 -0.63   3.207279
[4,] 2.345205 -30.28 0.27 125.7457 -0.63   2.104968
[5,] 2.405860 -30.28 0.27 128.6770 -0.63   3.264948

\[\widehat{\text{model}} = -30.28 + 0.27 \times \text{IQ} + -0.63 \times \text{motivation}\]

How far are we off?

error = study.outcome - model

cbind(model, study.outcome, error)[1:5,]

        model study.outcome       error
[1,] 2.753512      2.710330 -0.04318159
[2,] 2.775969      2.922617  0.14664823
[3,] 2.872561      1.997056 -0.87550534
[4,] 2.345205      2.322539 -0.02266610
[5,] 2.405860      2.162133 -0.24372667

Outcome = Model + Error

Is that true?

study.outcome == model + error

 [1] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
[16] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
[31] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE

Yes!

Visual

plot(study.outcome, xlab='personen', ylab='study.outcome')

n = length(study.outcome)
gemiddelde.study.outcome = mean(study.outcome)

## Voeg het gemiddelde toe
lines(c(1, n), rep(gemiddelde.study.outcome, 2))

## Wat is de totale variantie?
segments(1:n, study.outcome, 1:n, gemiddelde.study.outcome, col='blue')

## Wat zijn onze verwachte scores op basis van dit regressie model?
points(model, col='orange')

## Hoever zitten we ernaast, wat is de error?
segments(1:n, study.outcome, 1:n, model, col='purple', lwd=3)

Visual

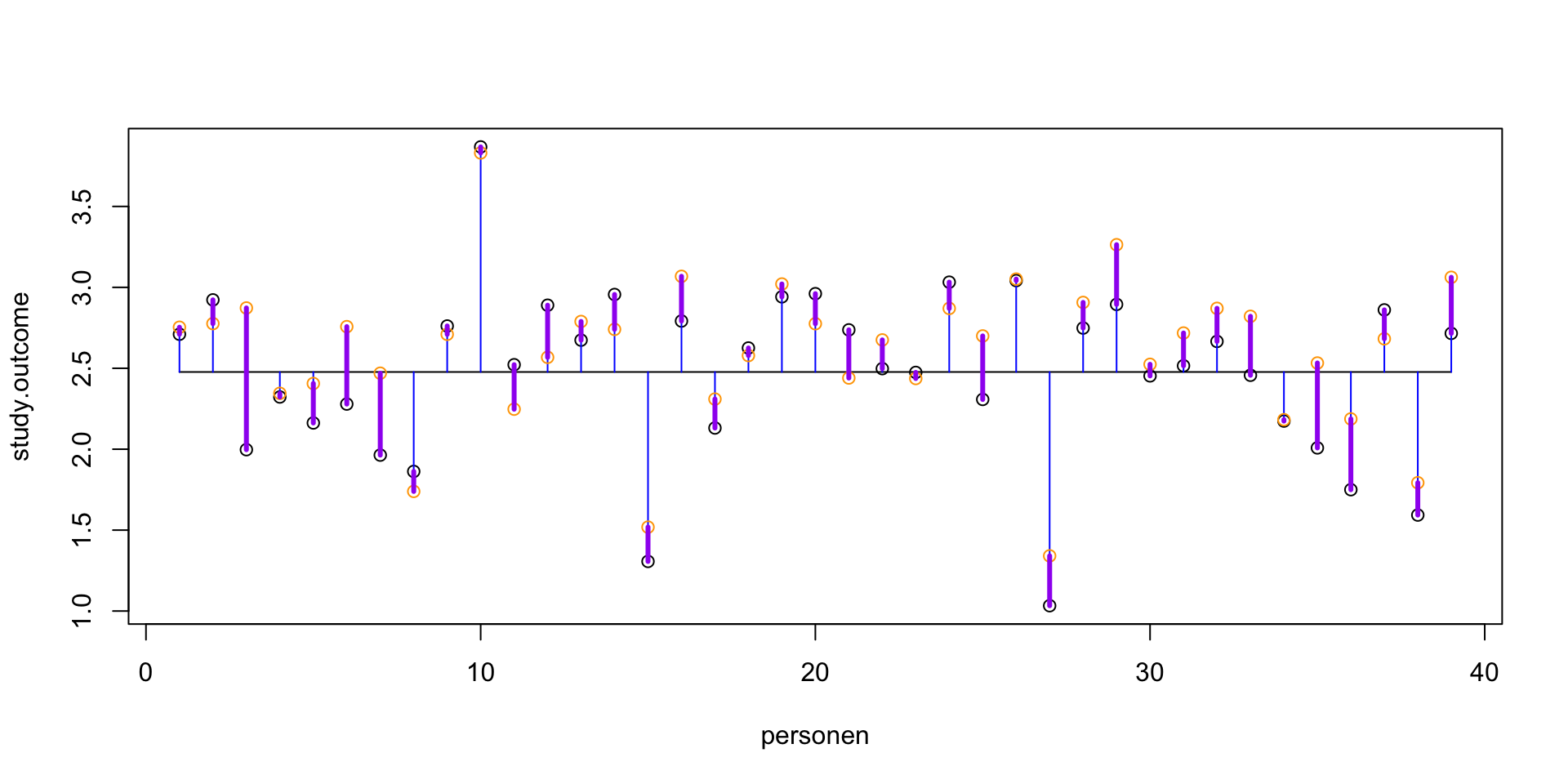
Explained variance

The explained variance is the deviation of the estimated model outcome compared to the total mean.

To get a percentage of explained variance, it must be compared to the total variance. In terms of squares:

\[\frac{{SS}_{model}}{{SS}_{total}}\]

We also call this: \(r^2\) of \(R^2\).

r = cor(study.outcome, model)
r^2

[1] 0.7527463

Compare models

fit1 <- lm(study.outcome ~ motivation, data)
fit2 <- lm(study.outcome ~ motivation + IQ, data)

# summary(fit1)
# summary(fit2)

anova(fit1, fit2)

Analysis of Variance Table

Model 1: study.outcome ~ motivation
Model 2: study.outcome ~ motivation + IQ
  Res.Df    RSS Df Sum of Sq      F    Pr(>F)    
1     37 4.3191                                  
2     36 2.6518  1    1.6673 22.635 3.144e-05 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

End

Contact

T-distribution & Multiple regression

T-distribution

Gosset

Population distribution

Population distribution

A sample

A sample

More samples

Mean and SE for all samples

Sampling distribution

Sampling distribution

T-statistic

t-value

Calculate t-values

Sampled t-values

Sampled t-values

T-distribution

One or two sided

Effect-size

Effect-sizes

Effect-size distribution

Power

Alpha Power

Alpha Power

Multiple regression

Multiple regression

Outcome vs Model

Outcome vs Model

Assumptions

Sensitivity

Homoscedasticity

Multicollinearity

Linearity

Example

Read data

Regression model in R

What is the model

Model summaries

Visual

What are the expected values based on this model

Apply regression model

How far are we off?

Outcome = Model + Error

Visual

Visual

Explained variance

Compare models

End

Contact

T-distribution &
Multiple regression