T-distribution and the
One-sample t-test

Klinkenberg

University of Amsterdam

20 sep 2022

T-distribution

Gosset

In probability and statistics, Student’s t-distribution (or simply the t-distribution) is any member of a family of continuous probability distributions that arises when estimating the mean of a normally distributed population in situations where the sample size is small and population standard deviation is unknown.

In the English-language literature it takes its name from William Sealy Gosset’s 1908 paper in Biometrika under the pseudonym “Student”. Gosset worked at the Guinness Brewery in Dublin, Ireland, and was interested in the problems of small samples, for example the chemical properties of barley where sample sizes might be as low as 3.

Source: Wikipedia

Population distribution

layout(matrix(c(2:6,1,1,7:8,1,1,9:13), 4, 4))

n  = 56    # Sample size
df = n - 1 # Degrees of freedom

mu    = 100
sigma = 15

IQ = seq(mu-45, mu+45, 1)

par(mar=c(4,2,2,0))  
plot(IQ, dnorm(IQ, mean = mu, sd = sigma), type='l', col="red", main = "Population Distribution")

n.samples = 12

for(i in 1:n.samples) {
  
  par(mar=c(2,2,2,0))  
  hist(rnorm(n, mu, sigma), main="Sample Distribution", cex.axis=.5, col="beige", cex.main = .75)
  
}

Population distribution

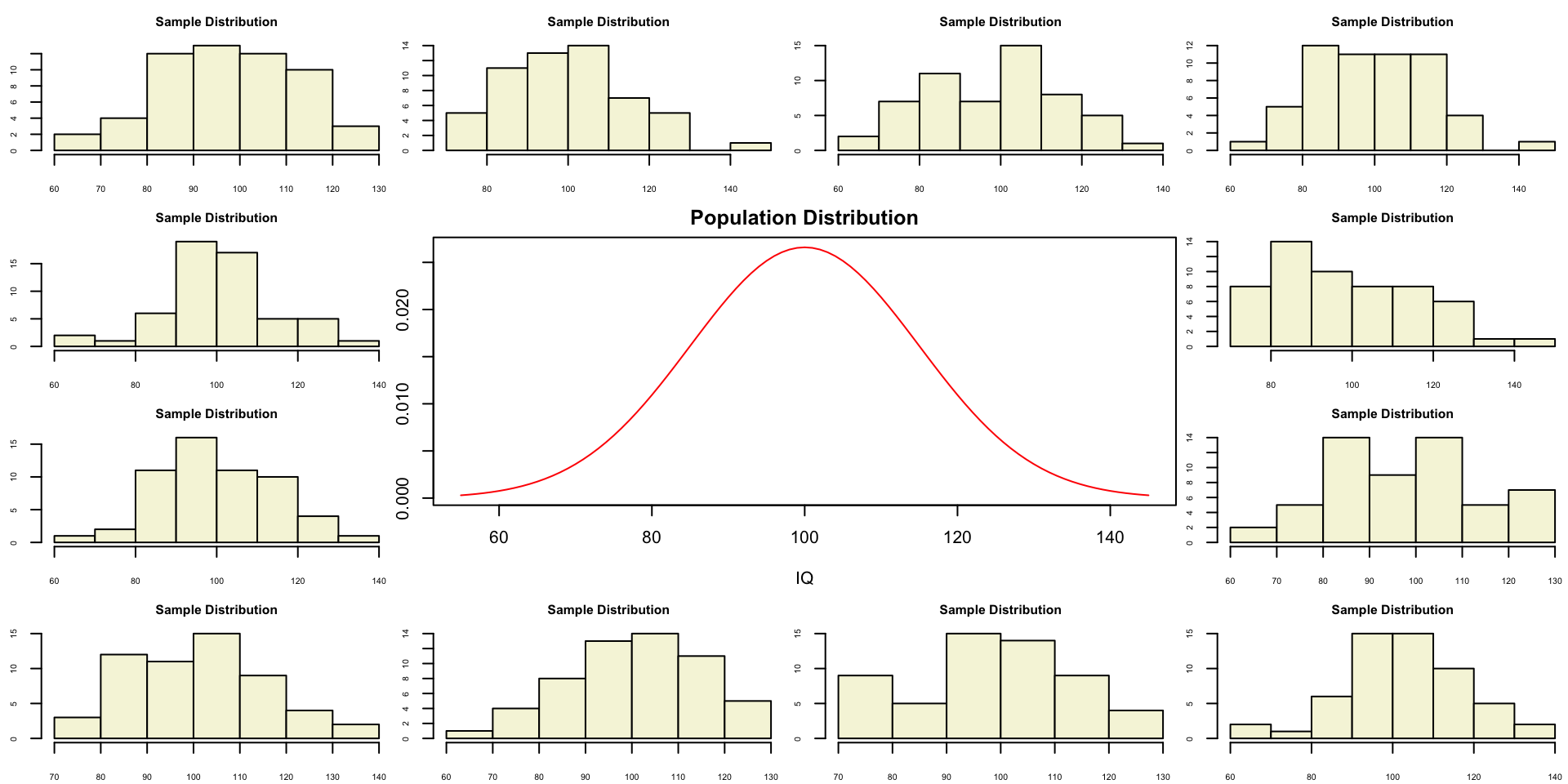
A sample

Let’s take one sample from our normal populatiion and calculate the t-value.

x = rnorm(n, mu, sigma); x

 [1]  90.29226  86.50468  82.67459  87.52014 109.47630  98.08283  87.67426
 [8] 104.11862  90.84647 102.19677 109.45225 108.74995 137.29301 104.96585
[15]  85.70202 100.49200  86.03716  87.62016 104.32542  98.36916 112.92071
[22]  96.43524  81.46636 111.04604 114.71462 135.98574  97.31552 100.96565
[29] 113.32101 101.34637  87.97518 102.77408 122.15193 103.17731  86.67964
[36] 105.05558 122.54113 117.60647 111.24434 101.70309 130.46728  98.23638
[43] 111.14123 104.96811  97.33341 100.28260  85.72114 107.43696 101.52655
[50] 101.63470 108.97211 117.24962  82.24049  87.62497 134.93508  63.65653

hist(x, main = "Sample distribution", col = "beige", breaks = 15)
text(80, 10, round(mean(x),2))

A sample

More samples

let’s take more samples.

n.samples     = 1000
mean.x.values = vector()
se.x.values   = vector()

for(i in 1:n.samples) {
  x = rnorm(n, mu, sigma)
  mean.x.values[i] = mean(x)
  se.x.values[i]   = (sd(x) / sqrt(n))
}

Mean and SE for all samples

head(cbind(mean.x.values, se.x.values))

     mean.x.values se.x.values
[1,]     100.24455    1.808818
[2,]      96.90638    1.588307
[3,]      99.68740    1.919229
[4,]      99.44906    2.463697
[5,]      97.76291    1.562652
[6,]     103.85461    2.099900

Sampling distribution

Of the mean

hist(mean.x.values, 
     col  = "beige", 
     main = "Sampling distribution", 
     xlab = "all sample means")

Sampling distribution

T-statistic

\[T_{n-1} = \frac{\bar{x}-\mu}{SE_x} = \frac{\bar{x}-\mu}{s_x / \sqrt{n}}\]

So the t-statistic represents the deviation of the sample mean \(\bar{x}\) from the population mean \(\mu\), considering the sample size, expressed as the degrees of freedom \(df = n - 1\)

t-value

\[T_{n-1} = \frac{\bar{x}-\mu}{SE_x} = \frac{\bar{x}-\mu}{s_x / \sqrt{n}}\]

t = (mean(x) - mu) / (sd(x) / sqrt(n))
t

[1] -0.2809564

Calculate t-values

\[T_{n-1} = \frac{\bar{x}-\mu}{SE_x} = \frac{\bar{x}-\mu}{s_x / \sqrt{n}}\]

t.values = (mean.x.values - mu) / se.x.values

tail(cbind(mean.x.values, mu, se.x.values, t.values))

        mean.x.values  mu se.x.values   t.values
 [995,]     102.68990 100    2.151975  1.2499683
 [996,]      98.13215 100    2.102059 -0.8885817
 [997,]      98.31403 100    1.927675 -0.8746117
 [998,]      95.94184 100    2.087404 -1.9441195
 [999,]     104.30809 100    1.918401  2.2456652
[1000,]      99.41000 100    2.099974 -0.2809564

Sampled t-values

What is the distribution of all these t-values?

hist(t.values, 
     freq = F, 
     main = "Sampled T-values", 
     xlab = "T-values",
     col  = "beige",
     ylim = c(0, .4))
T = seq(-4, 4, .01)
lines(T, dt(T,df), col = "red")
legend("topright", lty = 1, col="red", legend = "T-distribution")

Sampled t-values

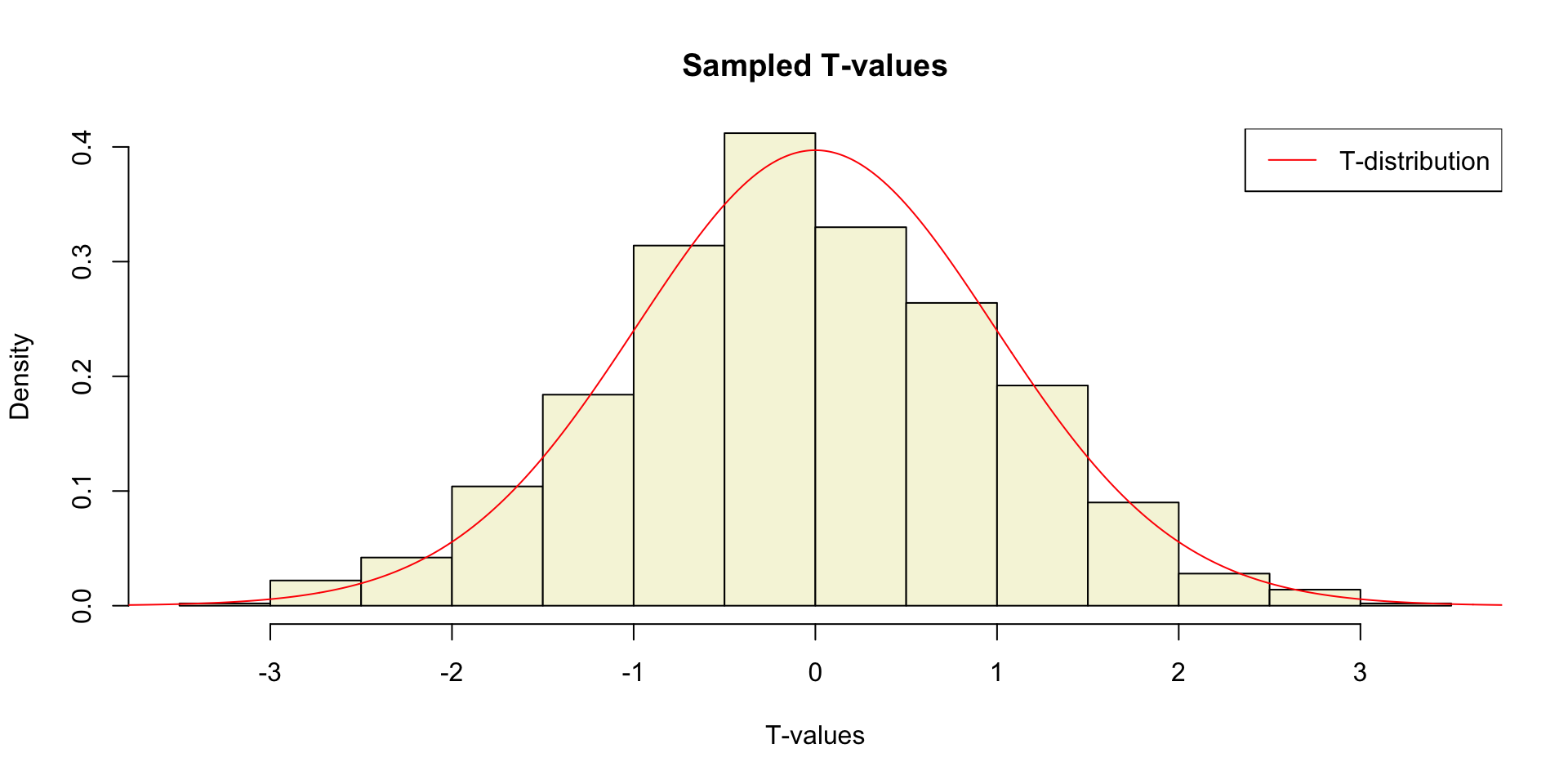
T-distribution

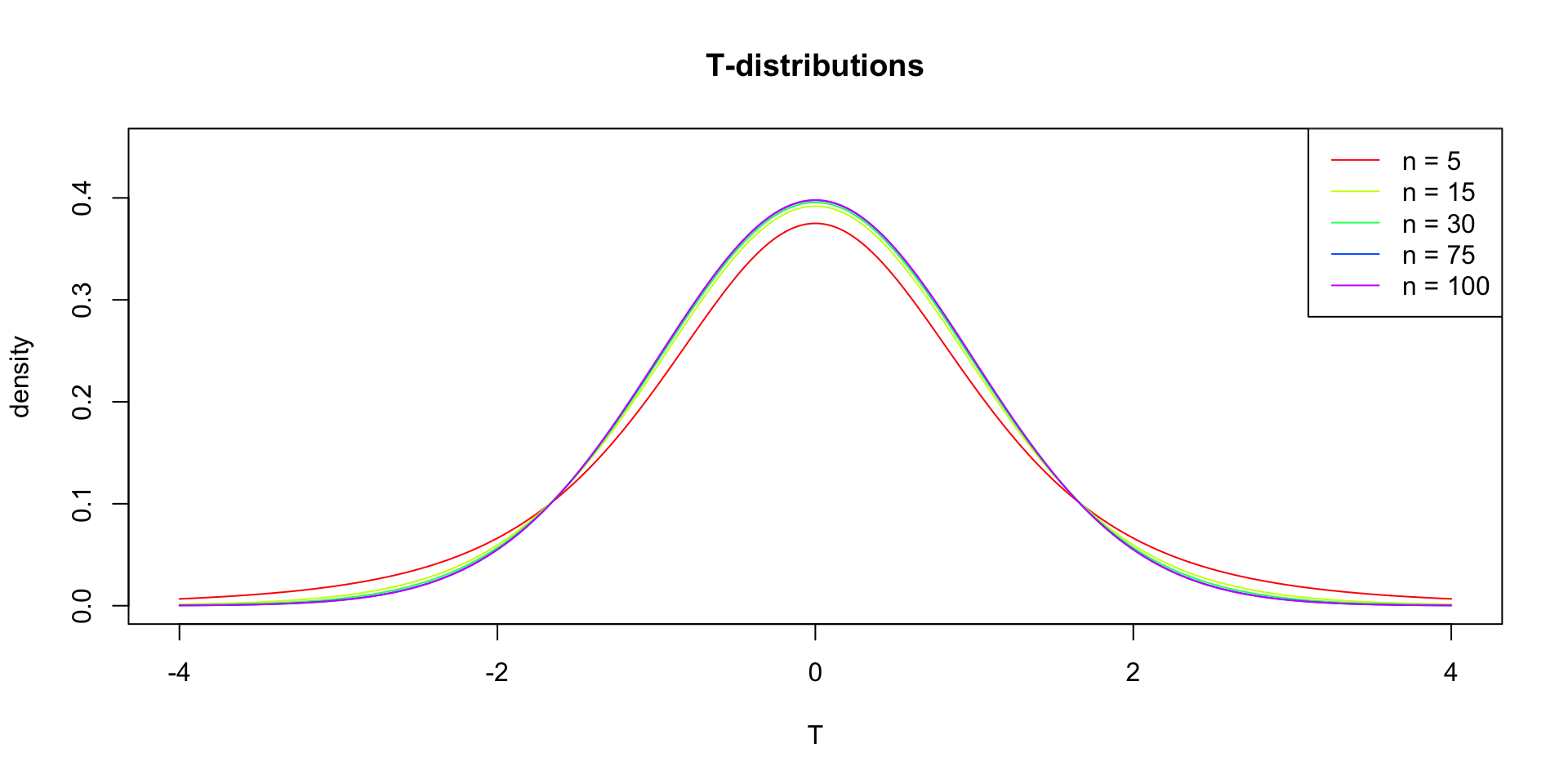
So if the population is normaly distributed (assumption of normality) the t-distribution represents the deviation of sample means from the population mean (\(\mu\)), given a certain sample size (\(df = n - 1\)).

The t-distibution therefore is different for different sample sizes and converges to a standard normal distribution if sample size is large enough.

The t-distribution is defined by:

\[\textstyle\frac{\Gamma \left(\frac{\nu+1}{2} \right)} {\sqrt{\nu\pi}\,\Gamma \left(\frac{\nu}{2} \right)} \left(1+\frac{x^2}{\nu} \right)^{-\frac{\nu+1}{2}}\!\]

where \(\nu\) is the number of degrees of freedom and \(\Gamma\) is the gamma function.

Source: wikipedia

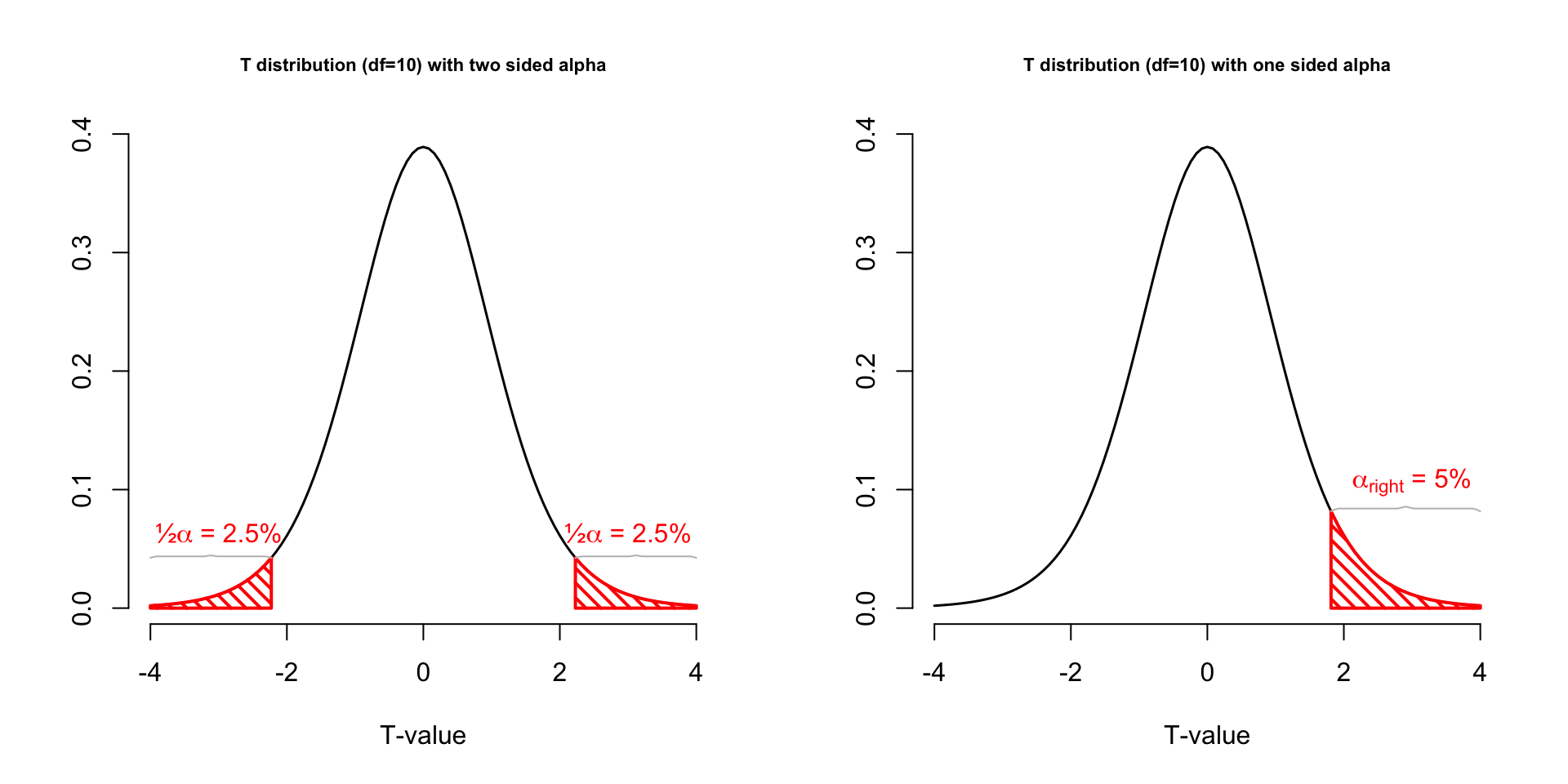
One or two sided

Two sided

\(H_A: \bar{x} \neq \mu\)

One sided

\(H_A: \bar{x} > \mu\)
\(H_A: \bar{x} < \mu\)

Effect-size

The effect-size is the standardised difference between the mean and the expected \(\mu\). In the t-test effect-size is expressed as \(r\).

\[r = \sqrt{\frac{t^2}{t^2 + \text{df}}}\]

r = sqrt(t^2/(t^2 + df))

r

[1] 0.2603778

Effect-sizes

We can also calculate effect-sizes for all our calculated t-values. Under the assumption of \(H_0\) the effect-size distribution looks like this.

        mean.x.values  mu se.x.values   t.values         r
 [995,]     102.68990 100    2.151975  1.2499683 0.1662015
 [996,]      98.13215 100    2.102059 -0.8885817 0.1189654
 [997,]      98.31403 100    1.927675 -0.8746117 0.1171210
 [998,]      95.94184 100    2.087404 -1.9441195 0.2535769
 [999,]     104.30809 100    1.918401  2.2456652 0.2898103
[1000,]      99.41000 100    2.099974 -0.2809564 0.0378570

Effect-size distribution

Cohen (1988)

Small: \(0 \leq .1\)
Medium: \(.1 \leq .3\)
Large: \(.3 \leq .5\)

Power

Strive for 80%
Based on know effect size
Calculate number of subjects needed
Use G*Power to calculate

Alpha Power

T = seq(-3,6,.01)
N = 45
E = 2

# Set plot
plot(0,0,
     type = "n",
     ylab = "Density",
     xlab = "T",
     ylim = c(0,.5),
     xlim = c(-3,6),
     main = "T-Distributions under H0 and HA")

critical_t = qt(.05,N-1,lower.tail=FALSE)

# Alpha
range_x = seq(critical_t,6,.01)
polygon(c(range_x,rev(range_x)),
        c(range_x*0,rev(dt(range_x,N-1,ncp=0))),
        col     = "grey",
        density = 10,
        angle   = 90,
        lwd     = 2)

# Power
range_x = seq(critical_t,6,.01)
polygon(c(range_x,rev(range_x)),
        c(range_x*0,rev(dt(range_x,N-1,ncp=E))),
        col     = "grey",
        density = 10,
        angle   = 45,
        lwd     = 2)

lines(T,dt(T,N-1,ncp=0),col="red", lwd=2) # H0 line
lines(T,dt(T,N-1,ncp=E),col="blue",lwd=2) # HA line

# Critical value
lines(rep(critical_t,2),c(0,dt(critical_t,N-1,ncp=E)),lwd=2,col="black")
text(critical_t,dt(critical_t,N-1,ncp=E),"critical T-value",pos=2, srt = 90)

# H0 and HA
text(0,dt(0,N-1,ncp=0),expression(H[0]),pos=3,col="red", cex=2)
text(E,dt(E,N-1,ncp=E),expression(H[A]),pos=3,col="blue",cex=2)

# Mu H0 line
lines(c(0,0),c(0,dt(0,N-1)), col="red",  lwd=2,lty=2)
text(0,dt(0,N-1,ncp=0)/2,expression(mu),pos=4,cex=1.2)
# Mu HA line
lines(c(E,E),c(0,dt(E,N-1,ncp=E)),col="blue",lwd=2,lty=2)
text(E,dt(0,N-1,ncp=0)/2,expression(paste(mu)),pos=4,cex=1.2)

# t-value
lines( c(critical_t+.01,6),c(0,0),col="green",lwd=4)

# Legend
legend("topright", c(expression(alpha),'POWER'),density=c(10,10),angle=c(90,45))

Alpha Power

R-Psychologist

One-sample t-test

IQ next to you

http://goo.gl/T6Lo2s

Models

\[\text{outcome} = \text{model} + \text{error}\]

Compare sample mean

We use the one-sample t-test to compare the sample mean \(\bar{x}\) to the population mean \(\mu\).

Let’s take a different sample and calculate the mean of this sample.

mu     = 120
n      = length(IQ.next.to.you)
x      = IQ.next.to.you
mean_x = mean(x, na.rm = TRUE)
sd_x   = sd(x, na.rm = TRUE)
cbind(n, mean_x, sd_x)

      n   mean_x     sd_x
[1,] 77 119.9091 12.71673

Does this mean, differ significantly from the population mean \(\mu = 120\)?

Hypothesis

Null hypothesis

\(H_0: \bar{x} = \mu\)

Alternative hypothesis

\(H_A: \bar{x} \neq \mu\)
\(H_A: \bar{x} > \mu\)
\(H_A: \bar{x} < \mu\)

Assumptions

Normal samples distribution
Random sample
Measurement level
- Interval
- Ratio

T-statistic

\[T_{n-1} = \frac{\bar{x}-\mu}{SE_x} = \frac{\bar{x}-\mu}{s_x / \sqrt{n}} = \frac{119.91 - 120 }{12.72 / \sqrt{77}}\]

So the t-statistic represents the deviation of the sample mean \(\bar{x}\) from the population mean \(\mu\), considering the sample size.

t = (mean_x - mu) / (sd_x / sqrt(n)); t

[1] -0.06273026

Type I error

To determine if this t-value significantly differs from the population mean we have to specify a type I error that we are willing to make.

Type I error / \(\alpha\) = .05

P-value one sided

Finally we have to calculate our p-value for which we need the degrees of freedom \(df = n - 1\) to determine the shape of the t-distribution.

df = n - 1; df

[1] 76

if(!"visualize" %in% installed.packages()) { install.packages("visualize") }
library("visualize")

visualize.t(t, df, section = "upper")

P-value one sided

P-value two sided

visualize.t(c(-t, t), df, section = "tails")

Effect-size

\[r = \sqrt{\frac{t^2}{t^2 + \text{df}}}\]

r = sqrt(t^2/(t^2 + df))

r

[1] 0.007195468

End

Contact

T-distribution and the One-sample t-test

T-distribution

Gosset

Population distribution

Population distribution

A sample

A sample

More samples

Mean and SE for all samples

Sampling distribution

Sampling distribution

T-statistic

t-value

Calculate t-values

Sampled t-values

Sampled t-values

T-distribution

One or two sided

Effect-size

Effect-sizes

Effect-size distribution

Power

Alpha Power

Alpha Power

One-sample t-test

IQ next to you

Models

Compare sample mean

Hypothesis

Null hypothesis

Alternative hypothesis

Assumptions

T-statistic

Type I error

P-value one sided

P-value one sided

P-value two sided

Effect-size

End

Contact

T-distribution and the
One-sample t-test