Paired and Independent
t-test

Klinkenberg

University of Amsterdam

22 sep 2022

Paired-samples t-test

Paired 2 samples

Paired-samples t-test

In the Paired samples t-test the deviation (\(D\)) for each pair is calculated and the mean of these deviations (\(\bar{D}\)) is tested against the null hypothesis where \(\mu = 0\).

\[t_{n-1} = \frac{\bar{D} - \mu}{ {SE}_D }\]

Where \(n\) (the number of cases) minus \(1\), are the degrees of freedom \(df = n - 1\) and \(SE_D\) is the standard error of \(D\), defined as \(s_D/\sqrt{n}\).

Hypothesis

\[\LARGE{ \begin{aligned} H_0 &: \bar{D} = \mu_D \\ H_A &: \bar{D} \neq \mu_D \\ H_A &: \bar{D} > \mu_D \\ H_A &: \bar{D} < \mu_D \\ \end{aligned}}\]

Data structure

index k1 k2
1 d d
2 d d
3 d d
4 d d

Where \(k\) is the level of the categorical predictor variabla and \(d\) is the value of the outcome/dependent variable.

Data example

We are going to use the IQ estimates we collected last week. You had to gues the IQ of the one sitting next to you and your own IQ.

Let’s take a look at the data.

IQ estimates

Calculate \(D\)

D = IQ.next.to.you - IQ.you

Calculate \(\bar{D}\)

D      = na.omit(D) # get rid of all missing values
D.mean = mean(D)
D.mean
[1] 1.959184

And we also need n.

n = length(D)
n
[1] 49

Calculate t-value

\[t_{n-1} = \frac{\bar{D} - \mu}{ {SE}_D }\]

mu = 0                # Define mu

D.sd = sd(D)          # Calculate standard deviation
D.se = D.sd / sqrt(n) # Calculate standard error

df   = n - 1          # Calculate degrees of freedom

# Calculate t
t = ( D.mean - mu ) / D.se
t
[1] 1.915726

Test for significance

Two tailed

if(!"visualize" %in% installed.packages()) { install.packages("visualize") }
library("visualize")

visualize.t(c(-t,t), df, section="tails")

Test for significance

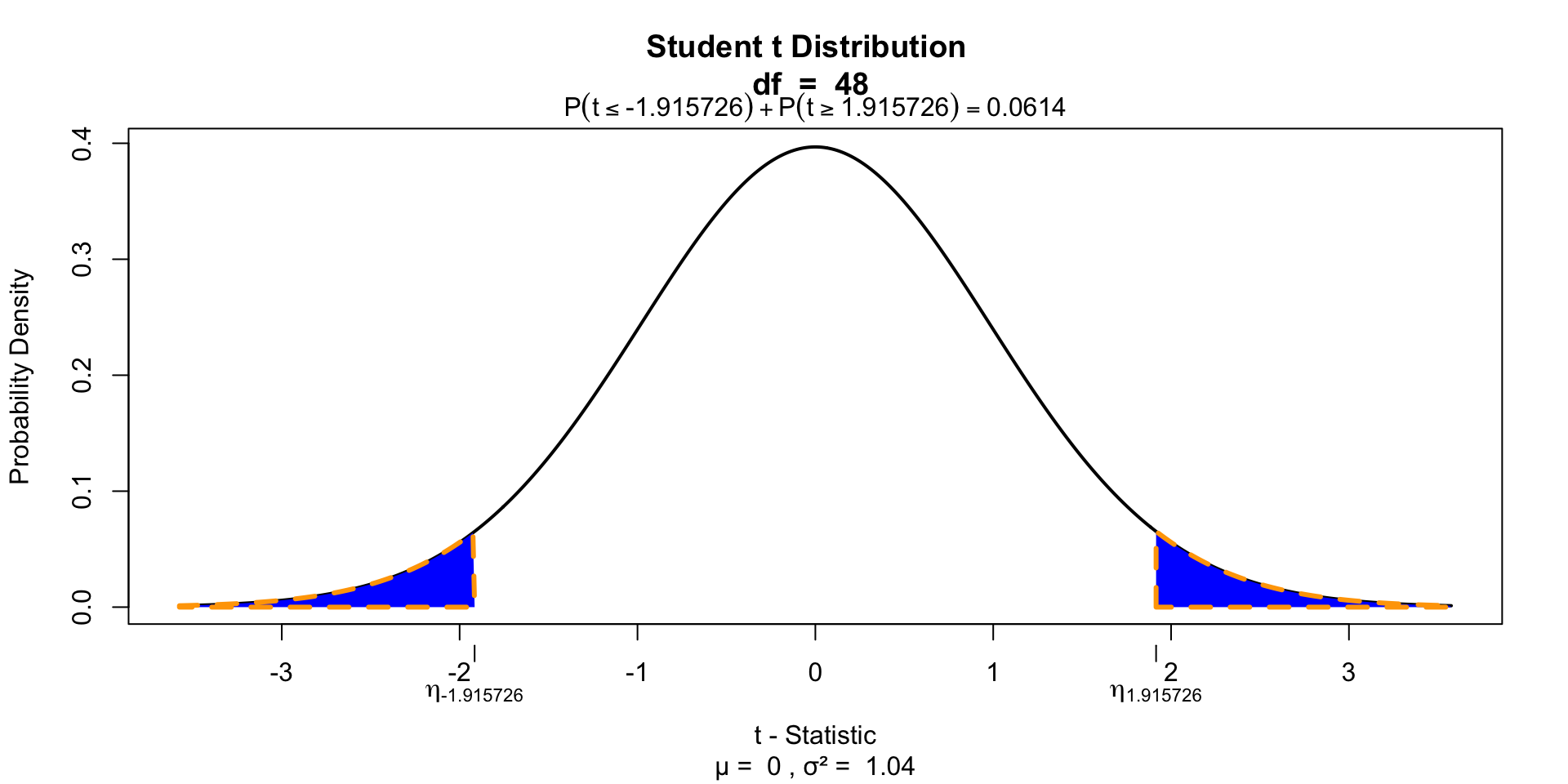
Effect-size

\[r = \sqrt{\frac{t^2}{t^2 + \text{df}}}\]

r = sqrt(t^2/(t^2 + df))
r
[1] 0.2665104

Confidence interval

To display correct conficance intervals in SPSS we need to correct the original scores for whithin subject variation.

** SPSS SYNTAX

COMPUTE personal_mean = MEAN(IQ.next.to.you, IQ.you).
EXECUTE.

AGGREGATE
  /OUTFILE=* MODE=ADDVARIABLES
  /BREAK=
  /total_mean = MEAN(personal_mean).

COMPUTE adjustment = total_mean - personal_mean.
EXECUTE.

COMPUTE IQ.next.to.you.adj = IQ.next.to.you + adjustment.
COMPUTE IQ.you             = IQ.you         + adjustment.
EXECUTE.

Independent-samples t-test

Compare 2 independent samples

Independent-samples t-test

In the independent-samples t-test the mean of both independent samples is calculated and the difference of these \((\bar{X}_1 - \bar{X}_2)\) means is tested against the null hypothesis where \(\mu = 0\).

\[t_{n_1 + n_2 -2} = \frac{(\bar{X}_1 - \bar{X}_2) - \mu}{{SE}_p}\]

Where \(n_1\) and \(n_2\) are the number of cases in each group and \(SE_p\) is the pooled standard error.

Hypothesis

\[\begin{aligned} H_0 &: t = 0 = \mu_t \\ H_A &: t \neq 0 \\ H_A &: t > 0 \\ H_A &: t < 0 \\ \end{aligned}\]

Data structure

index k outcome
1 1 d
2 1 d
3 2 d
4 2 d

Where \(k\) is the level of the categorical predictor variabla and \(d\) is the value of the outcome/dependent variable.

Additional assumption

Specificly for independent sample \(t\)-test.

  • Equality of variance
    • \(H_0\) : Variance \(=\) equal (\(p\) > .05)
    • \(H_A\) : Variance \(\neq\) equal (\(p\) < .05)

Example

We are going to use the IQ estimates we collected last week again. You had to gues the IQ of the one sitting next to you and your own IQ. But we are going to add gender to the data set. We did not register this so we are going to simulate some genders.

gender = sample(c("male", "female"), dim(data)[1], replace = TRUE)

The data

Calculate means

IQ.you.male   = subset(data, gender == "male",   select = IQ.you)$IQ.you
IQ.you.female = subset(data, gender == "female", select = IQ.you)$IQ.you

IQ.you.male.mean   = mean(IQ.you.male,   na.rm = T)
IQ.you.female.mean = mean(IQ.you.female, na.rm = T)

rbind(IQ.you.male.mean, IQ.you.female.mean)
                       [,1]
IQ.you.male.mean   121.8000
IQ.you.female.mean 119.3793

Calculate variance

IQ.you.male.var   = var(IQ.you.male,   na.rm = T)
IQ.you.female.var = var(IQ.you.female, na.rm = T)
rbind(IQ.you.male.var, IQ.you.female.var)
                      [,1]
IQ.you.male.var   59.95789
IQ.you.female.var 54.81527
IQ.you.male.n   = length(IQ.you.male)   - 1
IQ.you.female.n = length(IQ.you.female) - 1
rbind(IQ.you.male.n, IQ.you.female.n)
                [,1]
IQ.you.male.n     19
IQ.you.female.n   28

Calculate t-value

\[t_{n_1 + n_2 -2} = \frac{(\bar{X}_1 - \bar{X}_2) - \mu}{{SE}_p}\]

Where \({SE}_p\) is the pooled standard error.

\[{SE}_p = \sqrt{\frac{S^2_p}{n_1}+\frac{S^2_p}{n_2}}\]

And \(S^2_p\) is the pooled variance.

\[S^2_p = \frac{(n_1-1)s^2_1+(n_2-1)s^2_2}{n_1+n_2-2}\]

Where \(s^2\) is the variance and \(n\) the sample size.

Calculate pooled variance

\[S^2_p = \frac{(n_1-1)s^2_1+(n_2-1)s^2_2}{n_1+n_2-2}\]

df = IQ.you.male.n + IQ.you.female.n - 2

s2.p = ( (IQ.you.male.n-1)*IQ.you.male.var + (IQ.you.female.n-1)*IQ.you.female.var ) / df

df
[1] 45
s2.p
[1] 56.87232

Calculate pooled SE

\[ {SE}_p = \sqrt{\frac{S^2_p}{n_1}+\frac{S^2_p}{n_2}} \]

se.p = sqrt( ((s2.p/IQ.you.male.n) + (s2.p/IQ.you.female.n)) )
se.p
[1] 2.241525

Calculate t-value

\[t_{n_1 + n_2 -2} = \frac{(\bar{X}_1 - \bar{X}_2) - \mu}{{SE}_p}\]

t = ( IQ.you.male.mean - IQ.you.female.mean ) / se.p

t
[1] 1.07993

Test for significance

Two tailed

if(!"visualize" %in% installed.packages()) { install.packages("visualize") }
library("visualize")

visualize.t(c(-t,t), df, section="tails")

Test for significance

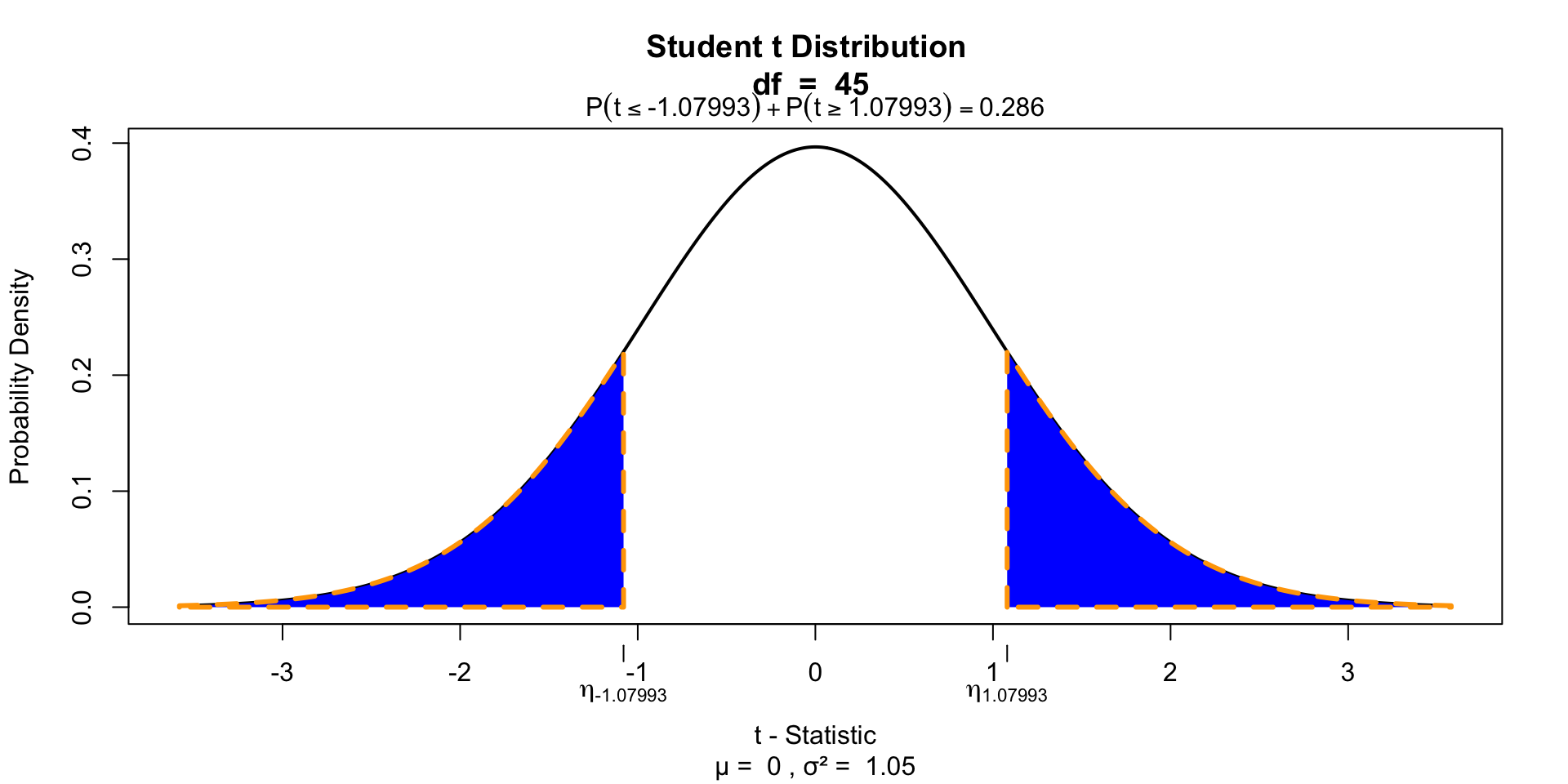
Effect-size

\[r = \sqrt{\frac{t^2}{t^2 + \text{df}}}\]

r = sqrt(t^2/(t^2 + df))

r
[1] 0.15894

End

Contact

CC BY-NC-SA 4.0

Scientific & Statistical Reasoning