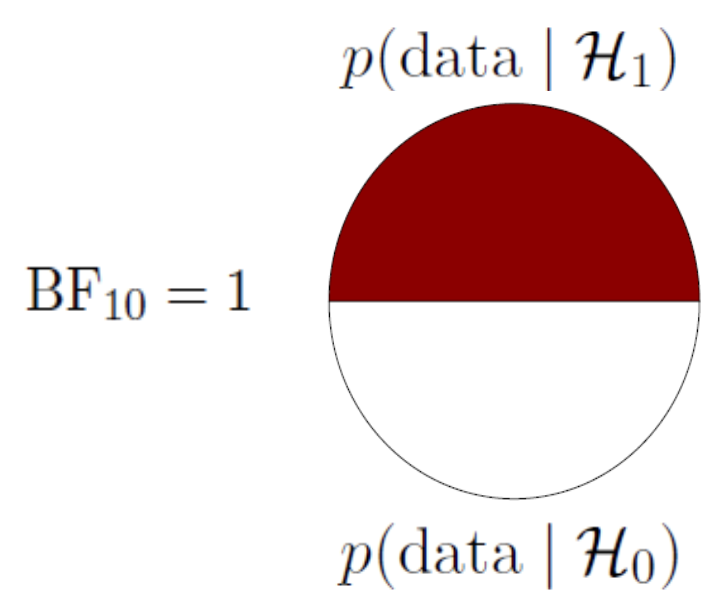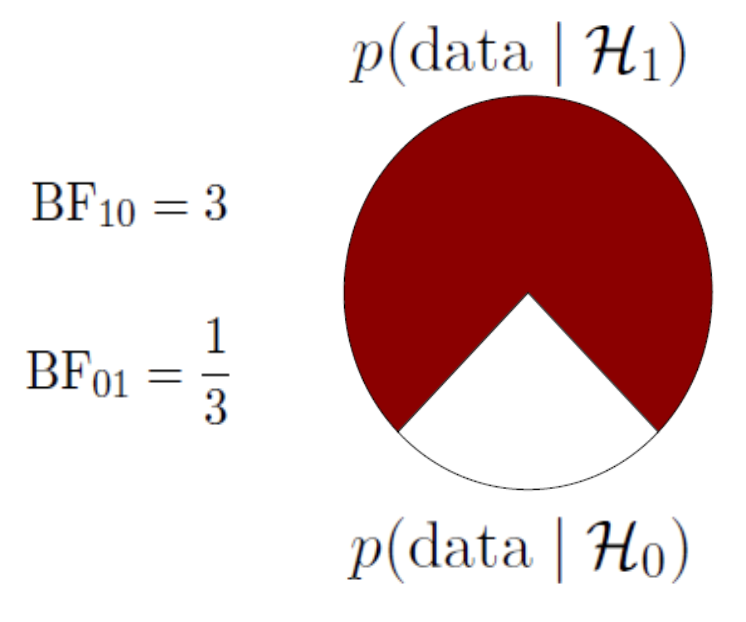
Bayes

Parameter estimation & hypothesis testing

Author

Klinkenberg

Published

October 21, 2022

Bayes Theorem

Bayes rule

\[\large P(A\mid B) = \frac{P(B \mid A) P(A)}{P(B)}\]

Conditional probabilities

\(P(A \mid B) = \frac{P(B \mid A) P(A)}{P(B)}\)

	\(P(A)\)	\(P(\neg A)\)
\(\begin{equation} \begin{aligned} P(\neg B) = & P(\neg B \mid A) P(A) + \\ & P(\neg B \mid \neg A) P(\neg A) \end{aligned} \end{equation}\)	\(P(\neg B \mid A)\)	\(P(\neg B \mid \neg A)\)
\(\begin{equation} \begin{aligned} P(B) = & P(B \mid A) P(A) + \\ & P(B \mid \neg A) P(\neg A) \end{aligned} \end{equation}\)	\(P(B \mid A)\)	\(P(B \mid \neg A)\)

Hypothesis | Data

\[\large P(H \mid D) = \frac{P(D \mid H) \times P(H)}{P(D)}\]

Posterior Likelihood Prior

\[\underbrace{P(H \mid D)}_{\text{Posterior}} = \underbrace{P(H)}_{\text{Prior}} \times \underbrace{\frac{P(D \mid H)}{P(D)}}_{\text{Likelihood}}\]

\(P(H)\), the \(prior\), is the initial degree of belief in \(H\).
\(P(H \mid D)\), the \(posterior\), is the degree of belief after incorporating news that \(D\) is true.
the quotient \(\frac{P(D \mid H)}{P(D)}\) represents the support \(D\) provides for \(H\).

Posterior \(\propto\) Likelihood \(\times\) Prior

Bayes is about

Posterior \(\propto\) Likelihood \(\times\) Prior

Quantified belief
Common sense expressed in numbers
Updating belief in light of new evidence
Yesterdays posteriors are todays priors

Generative model

Frequentists

State of the world → Data

Bayesions

Data → State of the world

Resources

Bayesian parameter estimation

Updating belief

Posterior \(\propto\) Likelihood \(\times\) Prior

So what is your belief

In lecture one I tossed ten times. with a coin that was supposedly healed after hamering it flat.

I arbitrarily assumed my \(H_A: \theta=.25\).

Considering all possible values of \(\theta\), what is your belief?

\([0,1] \Rightarrow \{\theta\in\Bbb R:0\le \theta\le 1\}\)

Draw your belief

Prior distribution

You have assigned a prior probability distribution to the parameter \(\theta\).

This is your prior

Now we normally do not draw our priors, but we could.

Priors

We can choose a flat prior, or a beta distributed prior with different parameter values \(a\) and \(b\).

theta = seq(0,1, .001)
layout(matrix(1:4,2,2))
plot(theta, dunif(theta),           type="l", ylab = "likelihood")
plot(theta, dbeta(theta, 3, 5),     type="l", ylab = "likelihood")
plot(theta, dbinom(25, 100, theta), type="l", ylab = "likelihood")
plot(theta, dbeta(theta, 2, 2),     type="l", ylab = "likelihood")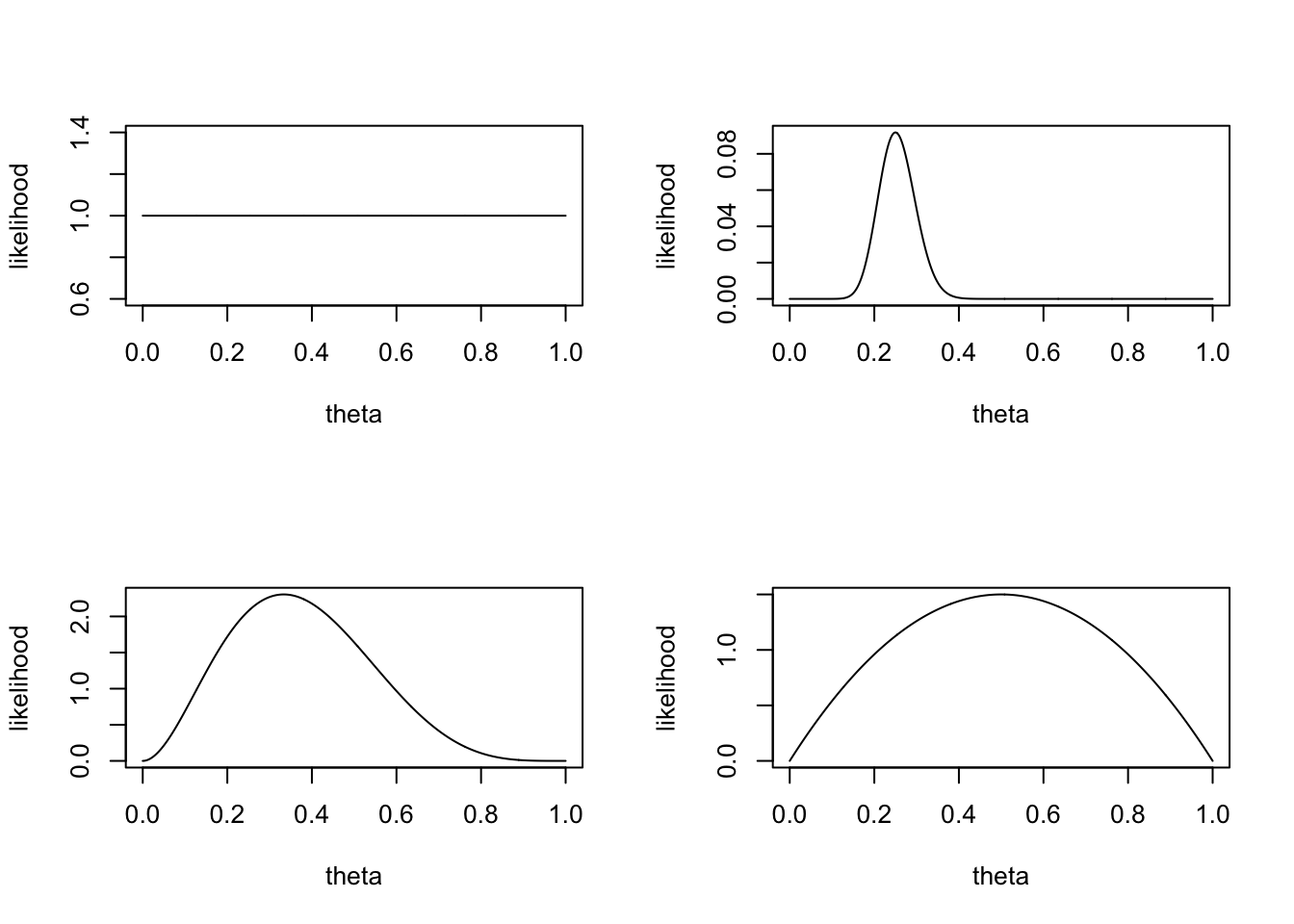

Choose prior

Binomial distribution

\(\theta^k (1-\theta)^{n-k} \\ \theta^{25} (1-\theta)^{100-25}\)

Now what is the data saying

My ten tosses

\(\begin{aligned} k &= 2 \\ n &= 10 \end{aligned}\)

k = 2
n = 10

Likelihood

What is the most likely parameter value \(\theta\) assuming the data to be true:

\(\theta = \frac{2}{10} = 0.2\)

theta.given.data = k/n

theta.given.data

[1] 0.2

Likelihood function

How likely is 2 out of 10 for all possible \(\theta\) values?

\(\theta^k (1-\theta)^{n-k}\)

thetas = seq(0, 1, .01)

likelihood =  dbinom(k, n, thetas)

plot(thetas, dbinom(k, n, thetas),
     main = "Likelihood function",
     type='l', 
     ylab = "Likelihood", 
     las = 1)
abline(v=theta.given.data, lty='dashed')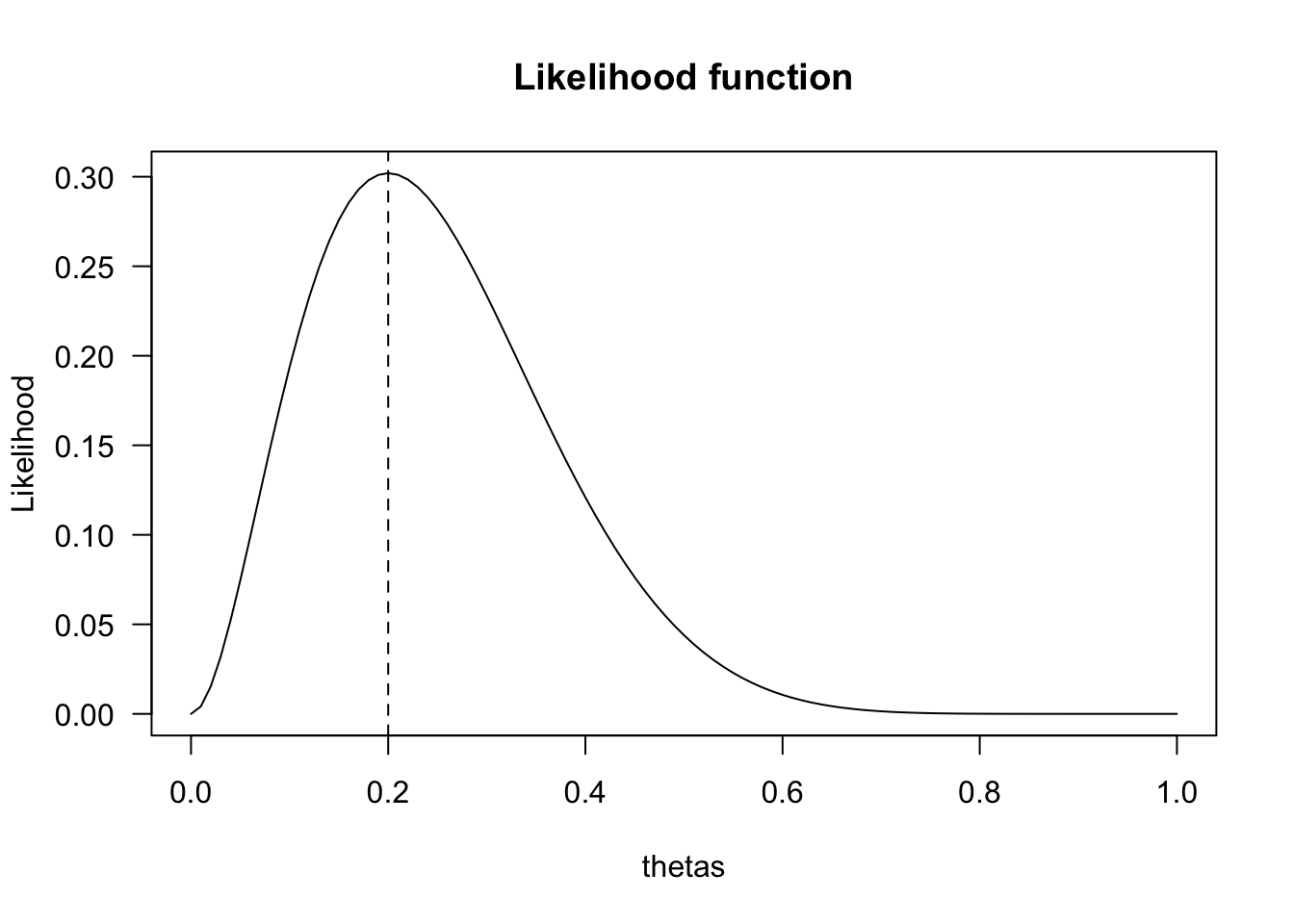

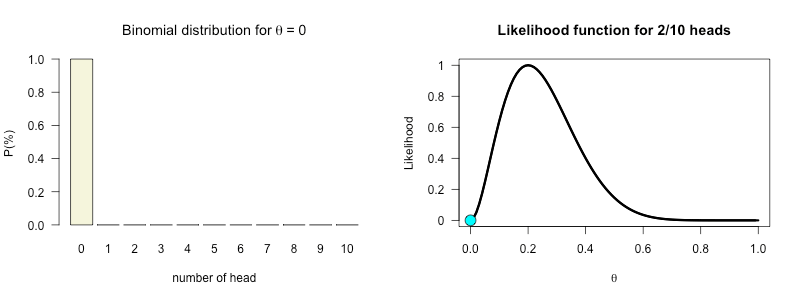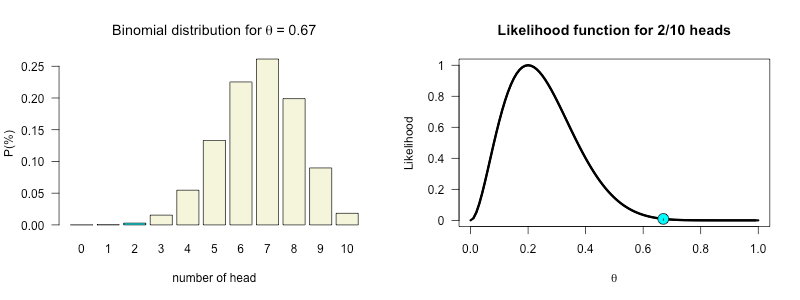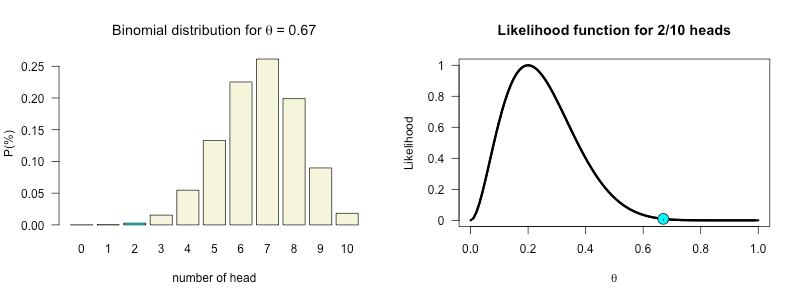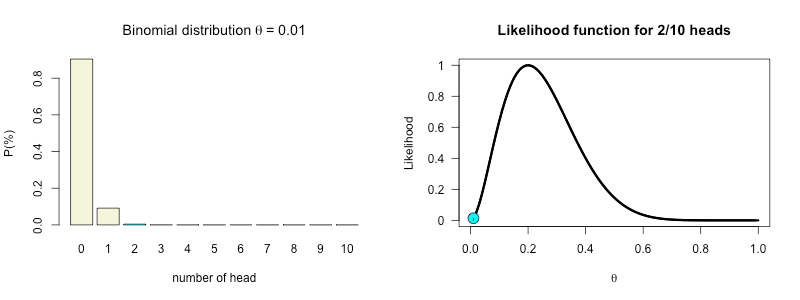
Posterior

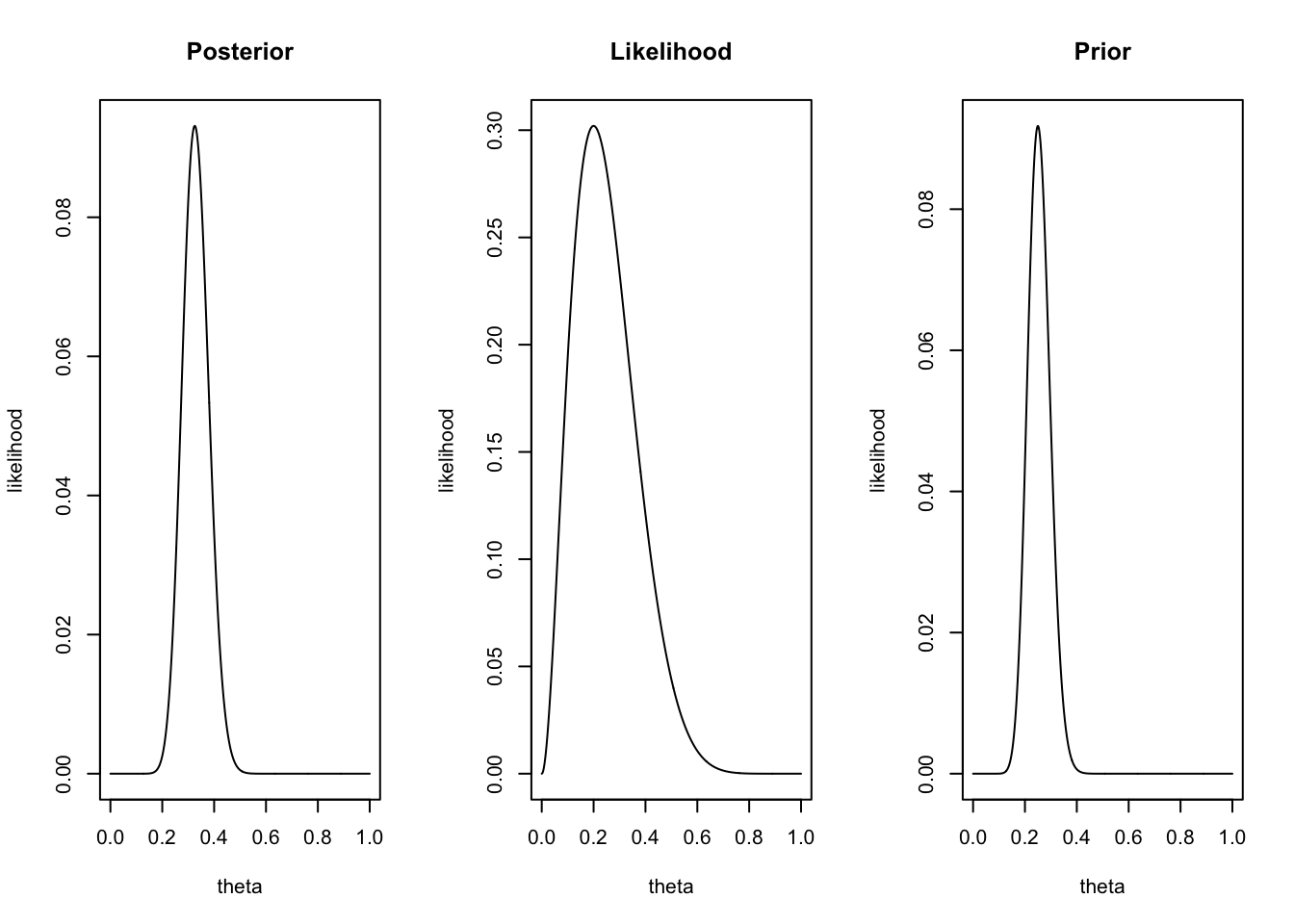
Now we can update our belief about the possible values of theta based on the data (the likelihood function) we found. For this we use Bayes rule.

\(\begin{aligned} {Posterior} &\propto {Likelihood} \times {Prior} \\ \theta^{27}(1-\theta)^{83} &= \theta^{2} (1-\theta)^{10-2} \times \theta^{25} (1-\theta)^{100-25} \end{aligned}\)

Visual

Theta all mighty

The true value of \(theta\) for our binomial distribution.

\(\Huge \theta = .68\)

The data driver!

Animation code

set.seed(25)
## Run multiple samples with our real theta of .68 as our driving force.
real.theta = .68

old.k = 27
old.n = 83

for(i in 1:20) {
  
  # Choose a random sample size between 10 and 100
  sample.size.n = sample(30:100, 1)
  # Sample number of heads based on sample size and fixed real parameter value
  number.of.heads.k = rbinom(1, sample.size.n, real.theta)
  
  # sample.size.n
  # number.of.heads.k
  
  new.k = old.k + number.of.heads.k
  new.n = old.n + sample.size.n
  
  layout(matrix(1:3,1,3))
  plot(theta, dbinom(new.k, new.n,  theta), type="l", ylab = "likelihood", main = "Posterior")
  plot(theta, dbinom(number.of.heads.k, sample.size.n,   theta), type="l", ylab = "likelihood", main = "Likelihood")
  plot(theta, dbinom(old.k, old.n, theta), type="l", ylab = "likelihood", main = "Prior")
  
  old.k = new.k
  old.n = new.n
  
}

Animation

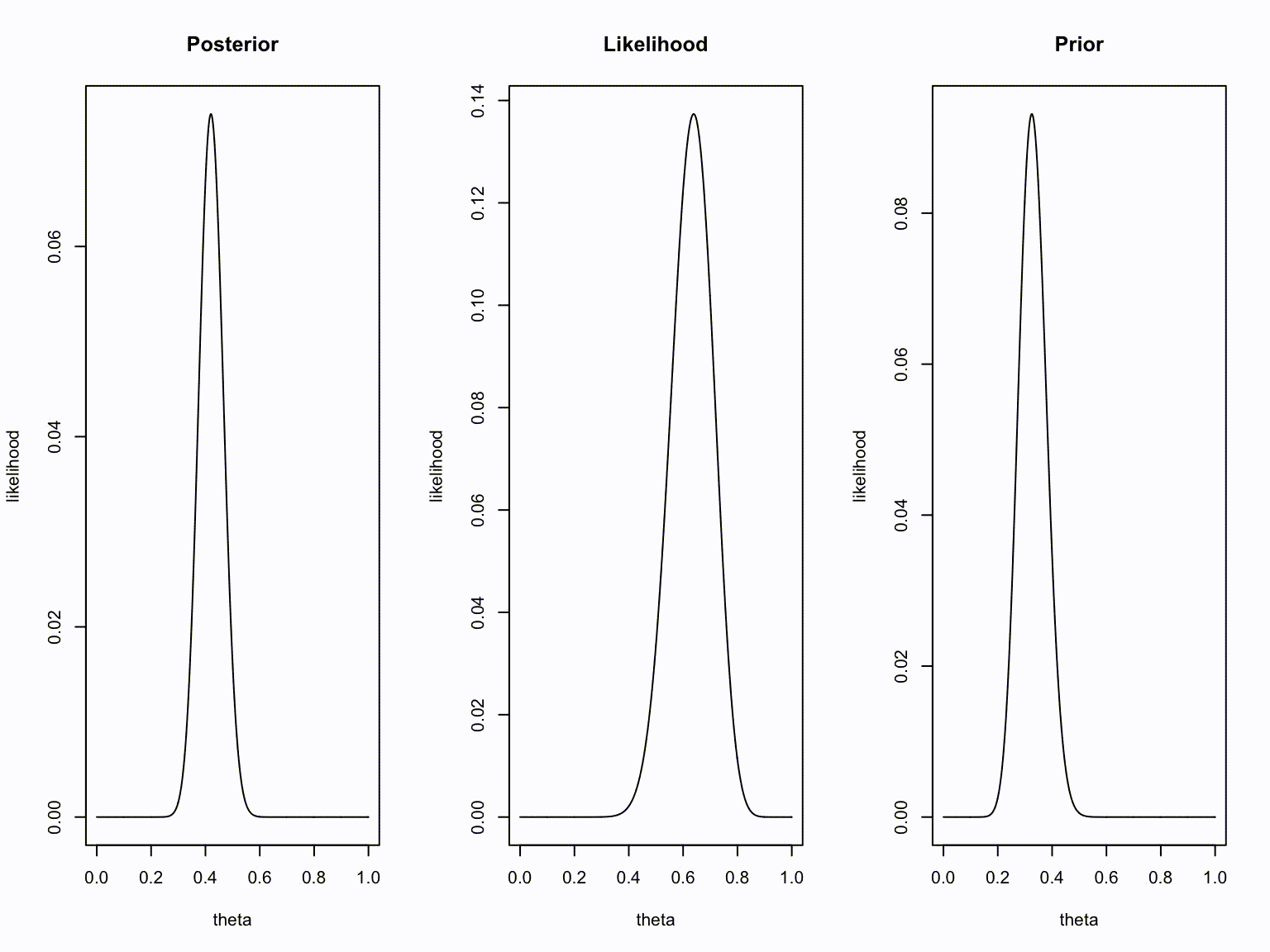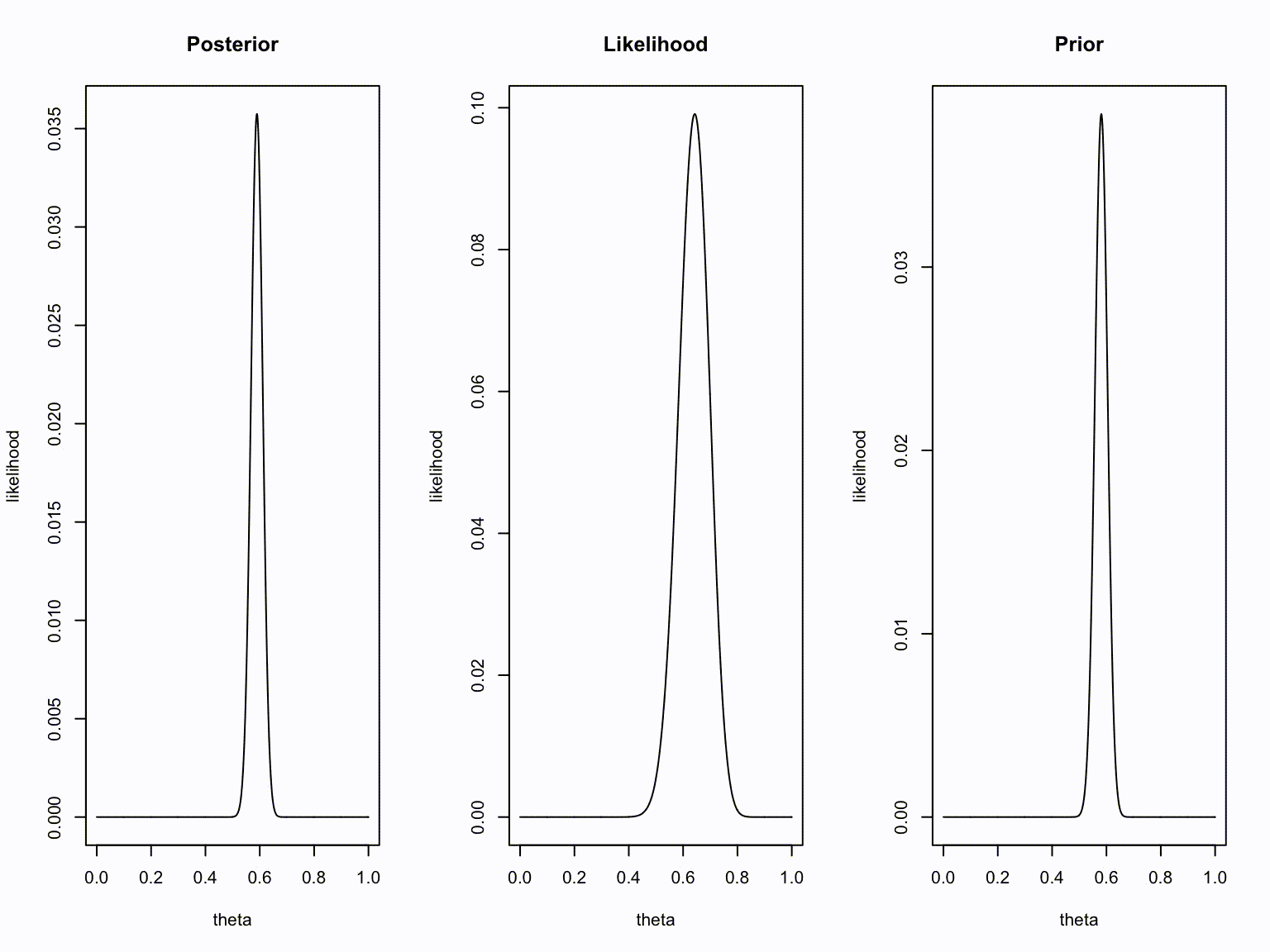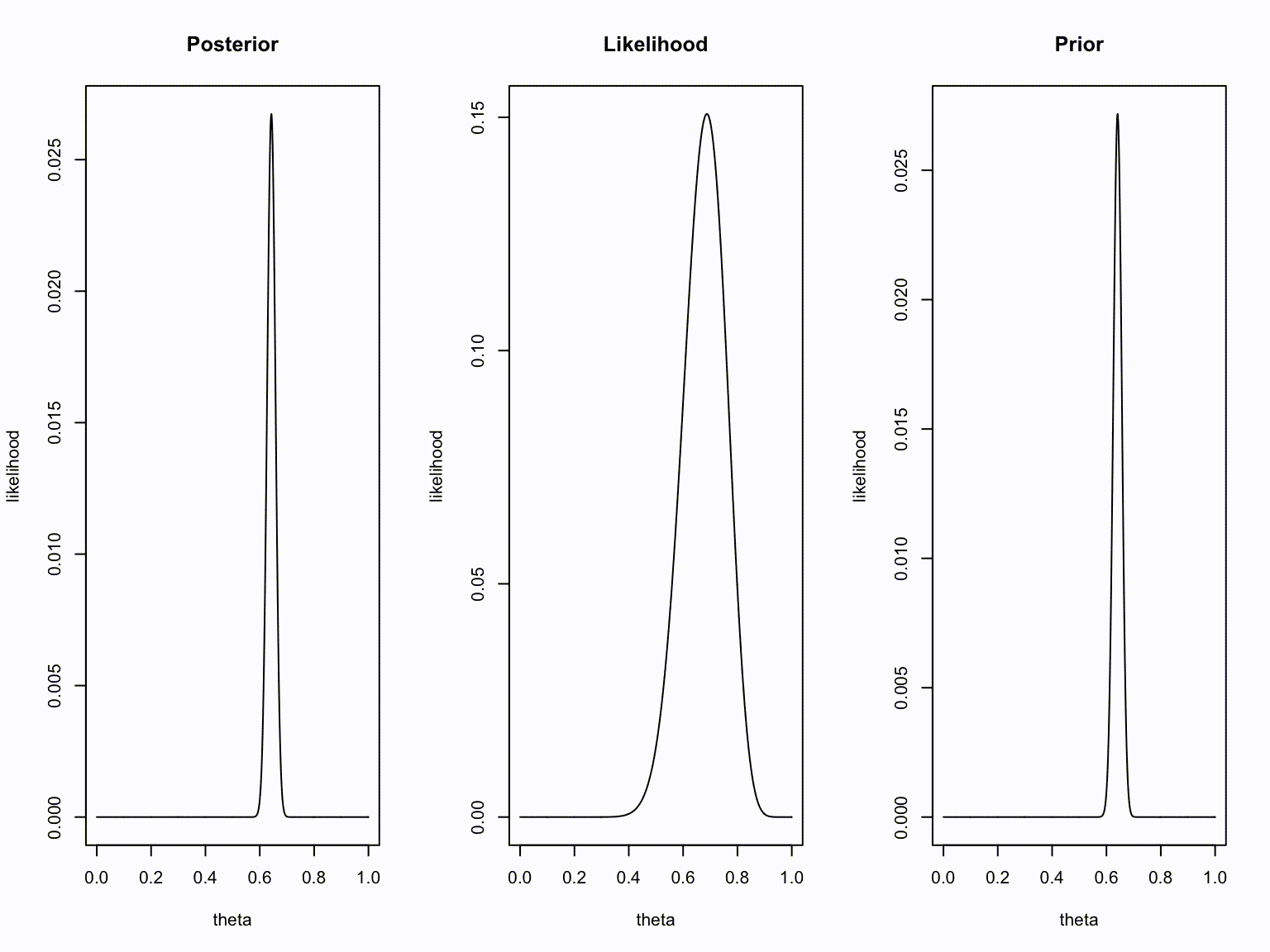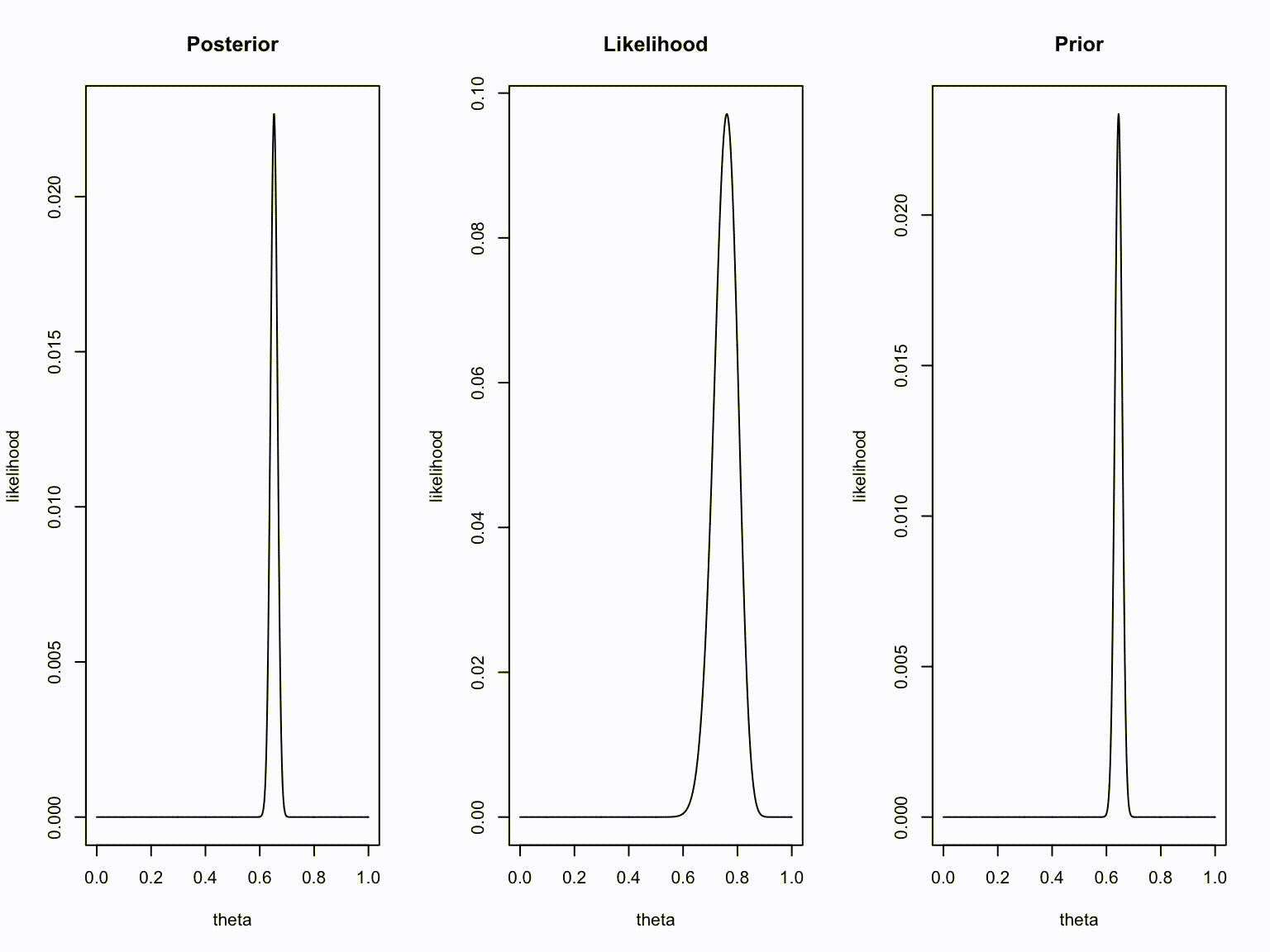
Take home message

Bayesians quantify uncertainty through distributions.
The more peaked the distribution, the lower the uncertainty.
Incoming information continually updates our knowledge; today’s posterior is tomorrow’s prior.

Bayesian hypothesis testing

Bayesion Hypothesis

\(H_0\), the null hypothesis. This is an invariance or “general law”. For instance \(\theta = 1\) (all swans are white) or \(\theta = .5\) (people cannot look into the future – performance is at chance).
\(H_A\) is the hypothesis that relaxes the restriction imposed by \(H_0\).

Prior Belief

\[\large \underbrace{\frac{P(H_A \mid data)}{P(H_0 \mid data)}}_\textrm{Posterior belief} = \underbrace{\frac{P(H_A)}{P(H_0)}}_\textrm{Prior belief} \times \underbrace{\frac{P(data \mid H_A)}{P(data \mid H_0)}}_\textrm{Bayes Factor}\]

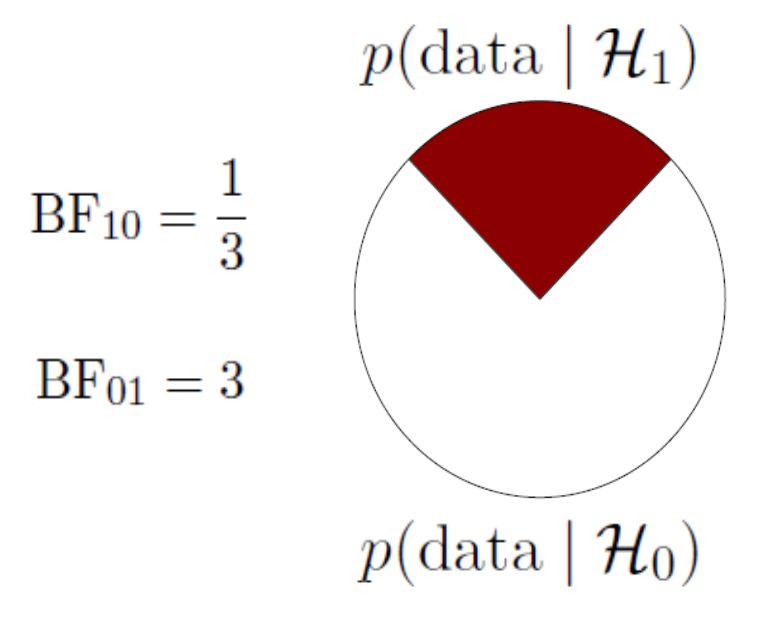
Bayes Factor

\[\underbrace{\frac{P(data \mid H_A)}{P(data \mid H_0)}}_\textrm{Bayes Factor}\]

A ratio of the likelihood of the data under the alternative and the null.

A Bayes factor of \({BF}_{10} = 3\), means that the data are 3 times more likely under the alternative than under the null.

Simple BF explanation

The special case of the Bayes Factor for null hypotheses testing can be visualised as the difference between the likelihood of the data at \(H_A\) / \(H_1\) and \(H_0\) at the parameter value that represents the null.

interactive BF

A First Lesson in Bayesian Inference - Shiny App by EJ

Heuristics for BF

Heuristics for the Interpretation of the Bayes Factor by Harold Jeffreys

BF	Evidence
1 – 3	Anecdotal
3 – 10	Moderate
10 – 30	Strong
30 – 100	Very strong
>100	Extreme

Advantages of the Bayes Factor

Provides a continuous degree of evidence without requiring an all-or-none decision.
Allows evidence to be monitored during data collection.
Differentiates between “the data support H0” (evidence for absence) and “the data are not informative” (absence of evidence).

BF pizza

JASP

A fresh way to do statistics

End

Contact