ANOVA

Repeated & Mixed

Klinkenberg

University of Amsterdam

18 oct 2022

ANOVA
One-way repeated

One-way repeated measures ANOVA

The one-way repeated measures ANOVA analyses the variance of the model while reducing the error by the within person variance.

1 dependent/outcome variable
1 independent/predictor variable
- 2 or more levels
All with same subjects

Assumptions

Uni- or Multivariate
Continuous dependent variable
Normaly distributed
- Shapiro-Wilk
Equality of variance within groups
- Mauchly’s test of Sphericity

Uni- or Multi- descision tree

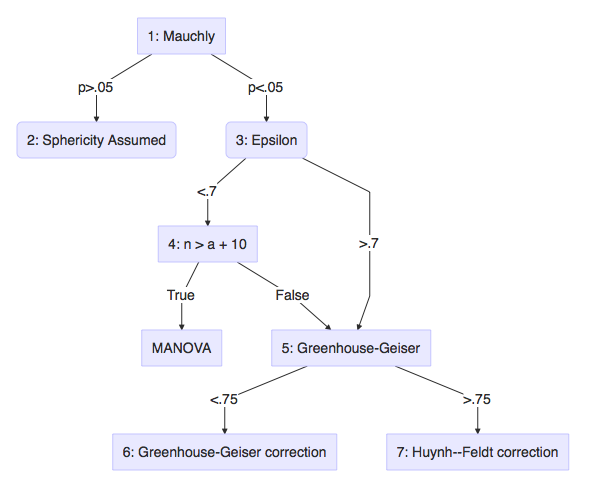
Field: 15.5.2, Output 15.2
Field: Output 15.4
Field: Jane Superbrain 15.2, Output 15.2 GG and HF.
Field: Jane Superbrain 15.2, Sample size \(n\) is larger than \(a\) (number of levels) + 10
Field: 15.5.4, Output 15.2
Field: 15.5.4, Output 15.4
Field: 15.5.4, Output 15.4

Formulas

Variance	Sum of Squares	df	Mean Squares	F-ratio
Between	\({SS}_{{between}} = {SS}_{{total}} - {SS}_{{within}}\)	\({DF}_{{total}}-{DF}_{{within}}\)	\(\frac{{SS}_{{between}}}{{DF}_{{between}}}\)
Within	\({SS}_{{within}} = \sum{s_i^2(n_i-1)}\)	\((n_i-1)n\)	\(\frac{{SS}_{{within}}}{{DF}_{{within}}}\)
• Model	\({SS}_{{model}} = \sum{n_k(\bar{X}_k-\bar{X})^2}\)	\(k-1\)	\(\frac{{SS}_{{model}}}{{DF}_{{model}}}\)	\(\frac{{MS}_{{model}}}{{MS}_{{error}}}\)
• Error	\({SS}_{{error}} = {SS}_{{within}} - {SS}_{{model}}\)	\((n-1)(k-1)\)	\(\frac{{SS}_{{error}}}{{DF}_{{error}}}\)
Total	\({SS}_{{total}} = s_{grand}^2(N-1)\)	\(N-1\)	\(\frac{{SS}_{{total}}}{{DF}_{{total}}}\)

Where \(n_i\) is the number of observations per person and \(k\) is the number of conditions. These two are equal for a one-way repeated ANOVA. Furthermore \(n\) is the number of subjects per condition and \(N\) is the total number of data points \(n \times k\).

Example

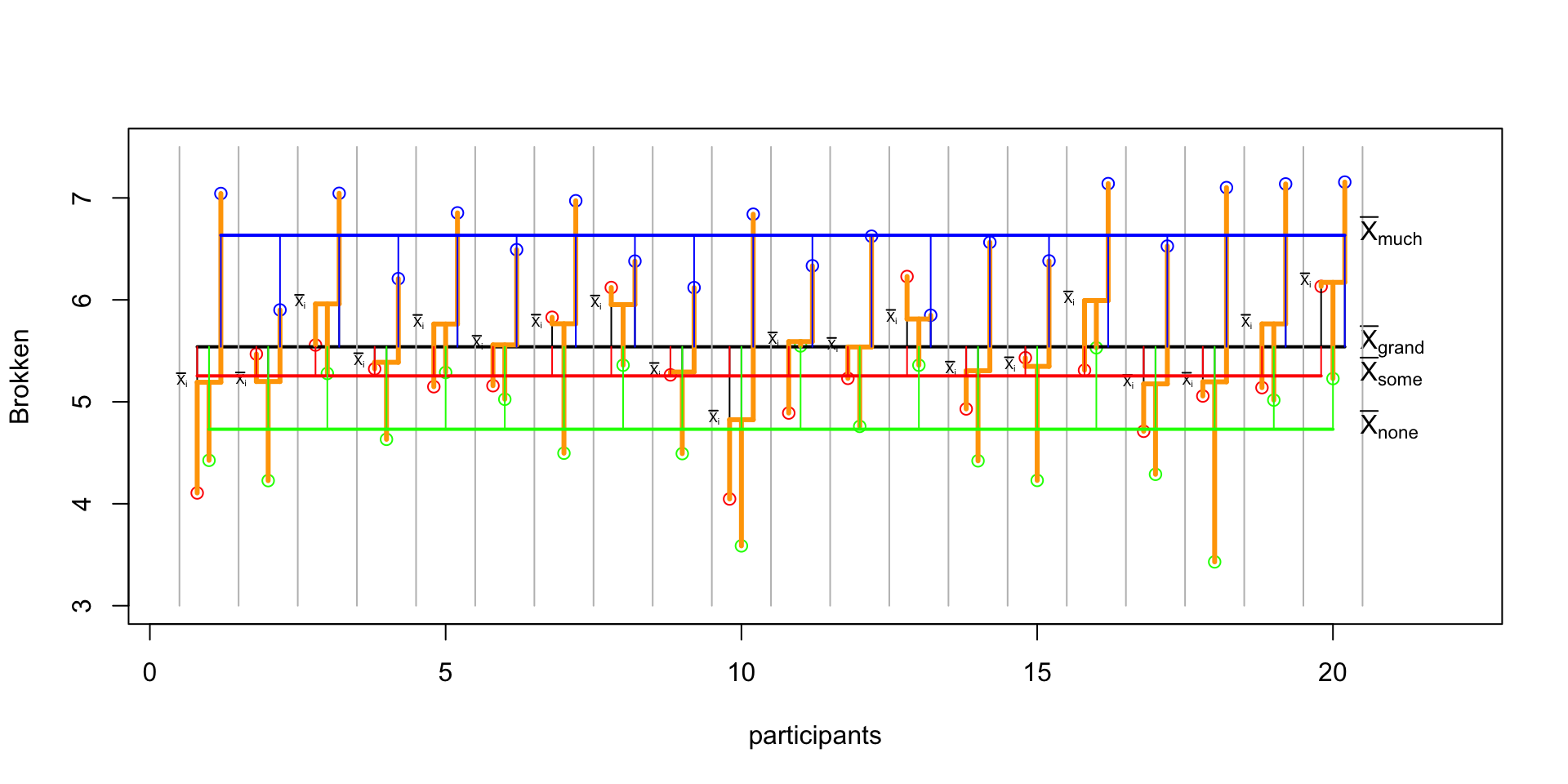
Measure driving ability in a driving simulator. Test in three consecutive conditions where participants come back to attend the next condition.

Alcohol none
Alcohol some
Alcohol much

The data

MS total

# Assign to individual variables
none_alc = data$none_alc
some_alc = data$some_alc
much_alc = data$much_alc
total    = c(none_alc,some_alc,much_alc)

\({MS}_{total} = \frac{{SS}_{{total}}}{{DF}_{{total}}} = s_{grand}^2\)

MS_total = var(total); MS_total

[1] 0.9410458

SS total

\({DF_{total}} = N-1\)

\({SS}_{{total}} = s_{grand}^2(N-1)\)

N = length(total)
DF_total = N - 1
SS_total = MS_total * DF_total; SS_total

[1] 55.5217

sum((total - mean(total))^2)

[1] 55.5217

SS total visual

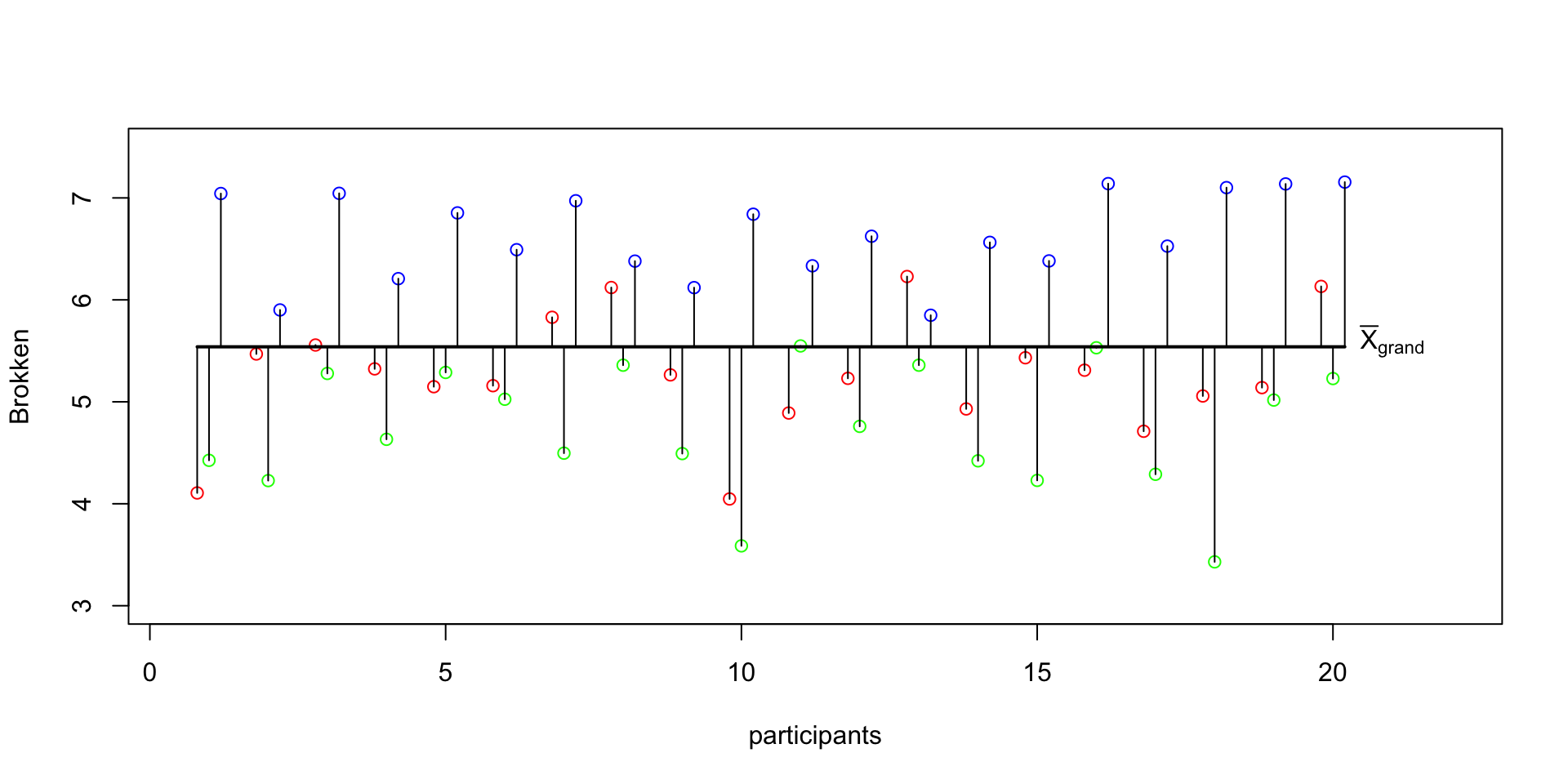
MS within

\({MS}_{within} = \frac{{SS}_{{within}}}{{DF}_{{within}}} \\ {DF}_{within} = (n_i-1)n\)

n.i = 3  # Number of mesurements per individual (none, some, much)
n   = 20 # Number of mesurements per group

DF_within = (n.i - 1) * n
DF_within

[1] 40

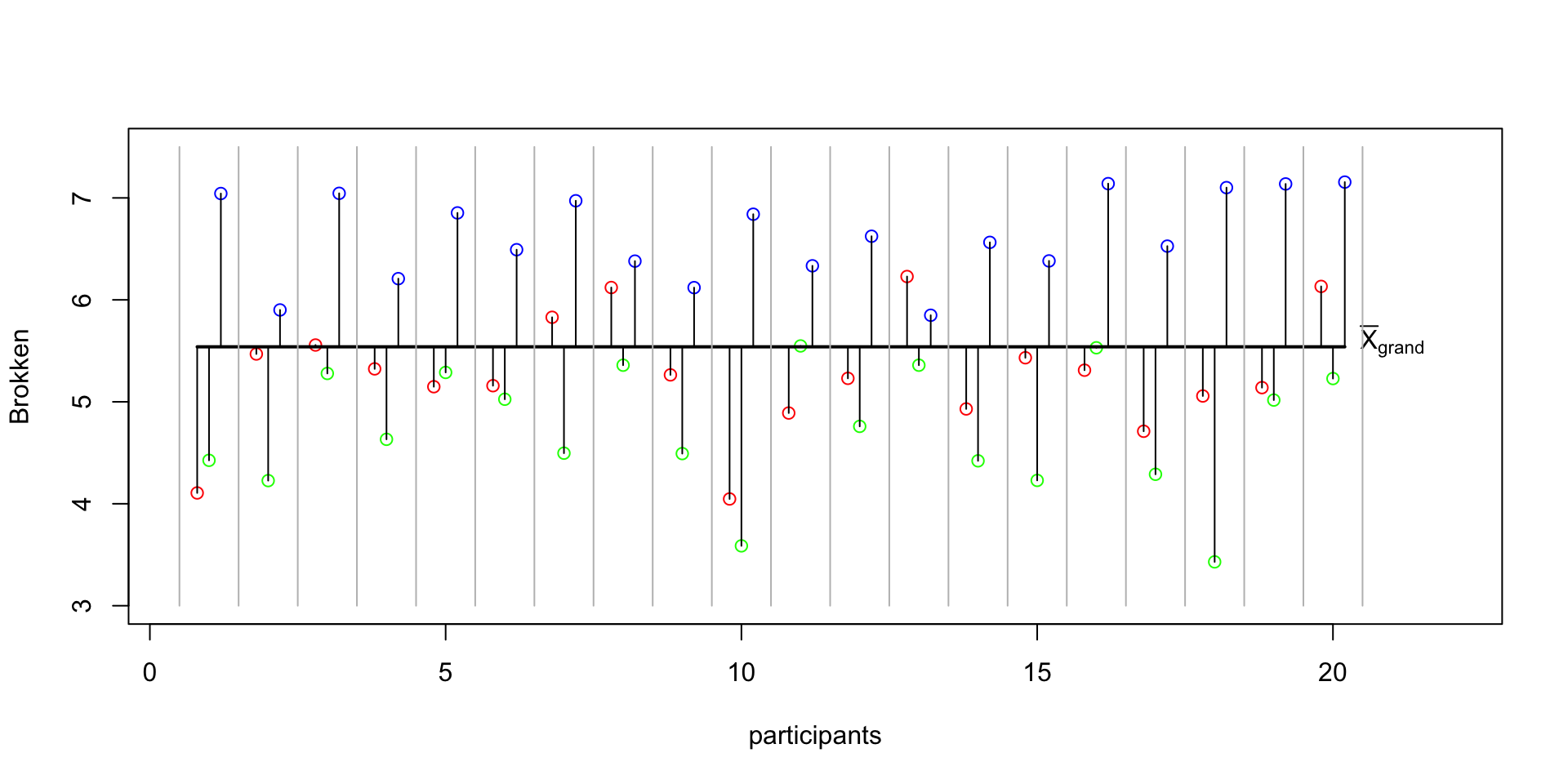
SS within

\({SS}_{{within}} = \sum{s_i^2(n_i-1)}\)

var_pp = apply(cbind(none_alc, some_alc, much_alc),1,var)
ss_pp  = var_pp * (n.i - 1)

SS_within = sum(ss_pp); SS_within

[1] 48.45032

mean_pp = apply(cbind(none_alc, some_alc, much_alc),1,mean)

sum(c((none_alc - mean_pp)^2, 
      (some_alc - mean_pp)^2,
      (much_alc - mean_pp)^2))

[1] 48.45032

SS within data

SS within visual

MS between

\({MS}_{between} = \frac{{SS}_{{between}}}{{DF}_{{between}}}\)

\({DF}_{between}-{DF}_{{within}} \\ {SS}_{between} = {SS}_{total} - {SS}_{within}\)

SS_between = SS_total - SS_within
SS_between

[1] 7.071382

DF_between = DF_total - DF_within
DF_between

[1] 19

MS model

\({MS}_{model} = \frac{{SS}_{{model}}}{{DF}_{{model}}} \\ {DF}_{model} = k-1\)

k = 3
DF_model = k - 1
DF_model

[1] 2

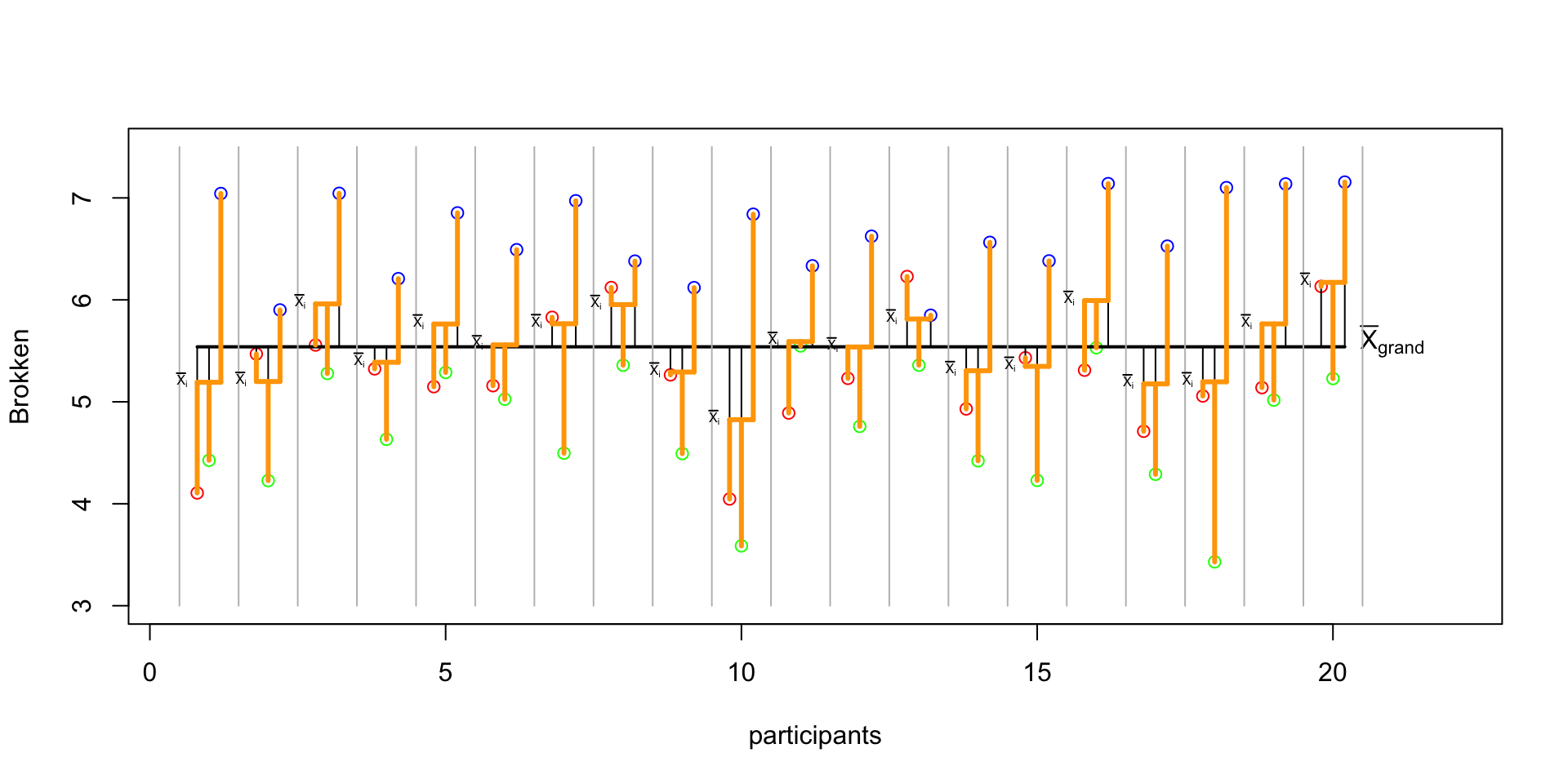
SS model

\({SS}_{model} = \sum{n_k(\bar{X}_k-\bar{X})^2}\)

# SS model
n_k1 = length(none_alc)
n_k2 = length(some_alc)
n_k3 = length(much_alc)

# Calculate sums of squares for the model
SS_k1 = n_k1 * (mean(none_alc) - mean(total))^2
SS_k2 = n_k2 * (mean(some_alc) - mean(total))^2
SS_k3 = n_k3 * (mean(much_alc) - mean(total))^2

SS_model = sum(SS_k1, SS_k2, SS_k3)
SS_model

[1] 38.63266

SS model visual

MS error

\(\frac{{SS}_{error}}{{DF}_{error}}\)

\({DF}_{error} = (n-1)(k-1)\)

DF_error = DF_within - DF_model
DF_error

[1] 38

SS error

\({SS}_{error} = {SS}_{within} - {SS}_{model}\)

SS_error = SS_within - SS_model
SS_error

[1] 9.817655

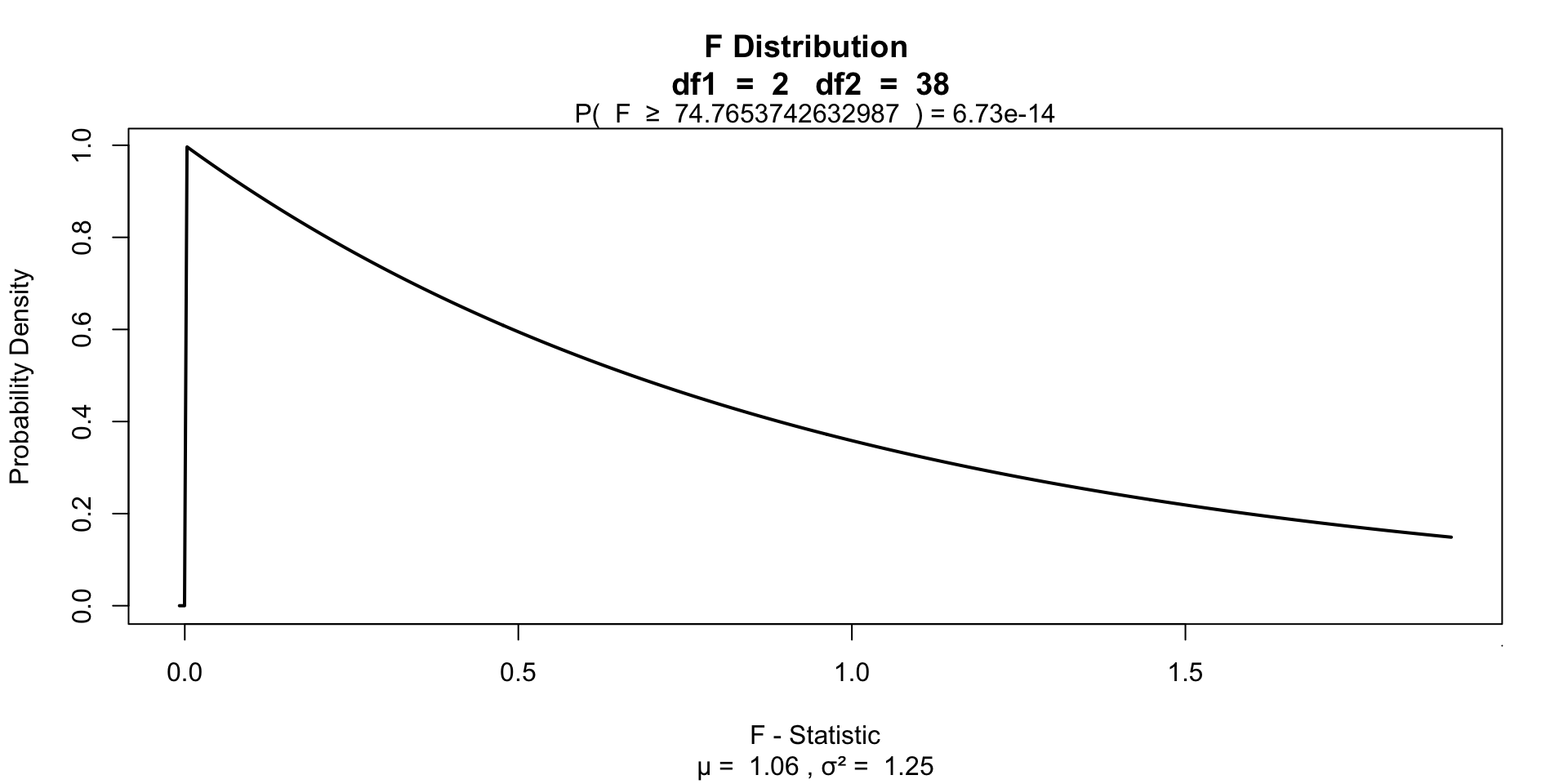
F ratio

\(F = \frac{{MS}_{{model}}}{{MS}_{{error}}}\)

# Calculate mean squares
MS_model = SS_model / DF_model
MS_error = SS_error / DF_error

# Calculate F statistic
F = MS_model / MS_error
F

[1] 74.76537

Visualize

library('visualize')
visualize.f(F, DF_model, DF_error, section="upper")

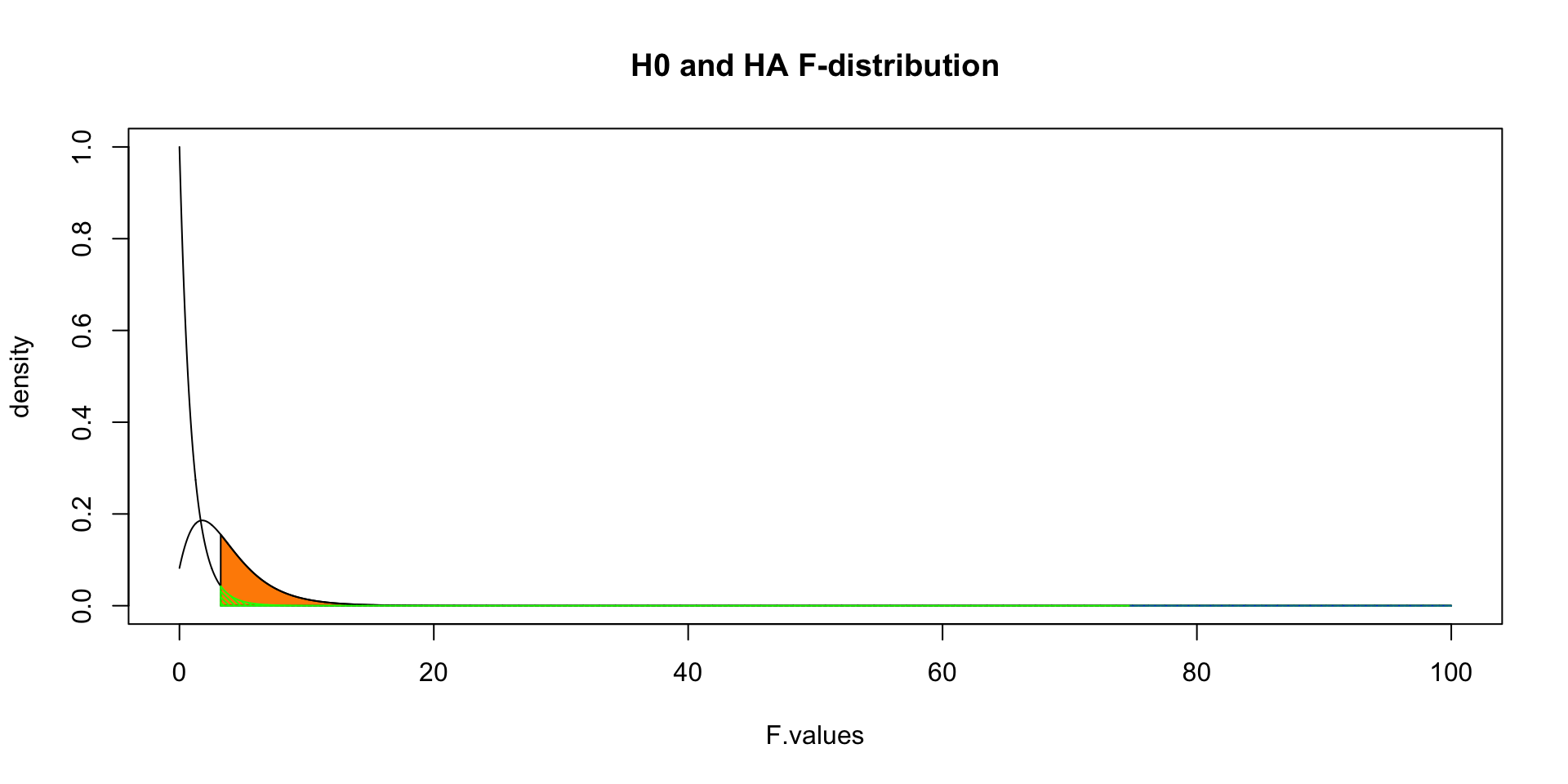
Contrast

Planned comparisons

Exploring differences of theoretical interest
Higher precision
Higher power

Post-Hoc

Unplanned comparisons

Exploring all possible differences
Adjust T value for inflated type 1 error

Effect size

General effect size measures

Amount of explained variance \(R^2\) also called eta squared \(\eta^2\).
Omega squared \(\omega^2\)

Effect sizes of contrasts or post-hoc comparisons

Cohen’s \(r\) gives the effect size for a specific comparison
- \(r_{Contrast} = \sqrt{\frac{t^2}{t^2+{df}}}\)
- \(r_{Contrast} = \sqrt{\frac{F(1,{df}_R)}{F(1,{df}_R)+{df}_R}}\)

ANOVA factorial repeated

Factorial repeated measures ANOVA

The factorial repeated measures ANOVA analyses the variance of the model while reducing the error by the within person variance.

1 dependent/outcome variable
2 or more independent/predictor variable
- 2 or more levels
All with same subjects

Assumptions

Same as one-way repeated measures ANOVA

Example

In this example we will again look at the amount of accidents in a car driving simulator while subjects where given varying doses of speed and alcohol. But this time we lat participants partake in all conditions. Every week subjects returned for a different experimental condition.

Dependent variable
- Accidents
Independent variables
- Speed
  - None
  - Small
  - Large
- Alcohol
  - None
  - Small
  - Large

person	1_1	1_2	1_3	2_1	2_2	2_3	3_1	3_2	3_3
1	1
2		2
3			3
4				4
5					5
6						6
7							7
8								8
9									9

Data

Mixed design ANOVA

Mixed design

The mixed ANOVA analyses the variance of the model while reducing the error by the within person variance.

1 dependent/outcome variable
2 or more independent/predictor variable with different subjects
- 2 or more levels
1 or more independent/predictor variable with same subjects
- 2 or more levels

Assumptions

Same as repeated measures ANOVA and same as factorial ANOVA.

Example

Dependent variable
- Accidents
Independent variables
- Speed (same subjects)
  - None
  - Small
  - Large
- Alcohol (same subjects)
  - None
  - Small
  - Large
- Gender
  - Males
  - Females

person	gender	1_1	1_2	1_3	2_1	2_2	2_3	3_1	3_2	3_3
1	males	1
2	males		2
3	males			3
4	males				4
5	males					5
6	males						6
7	males							7
8	males								8
9	males									9
10	females	1
12	females		2
13	females			3
14	females				4
15	females					5
16	females						6
17	females							7
18	females								8
20	females									9

Data

End

Contact

ANOVA

ANOVAOne-way repeated

One-way repeated measures ANOVA

Assumptions

Uni- or Multi- descision tree

Formulas

Example

The data

MS total

SS total

SS total visual

MS within

SS within

SS within data

SS within visual

MS between

MS model

SS model

SS model visual

MS error

SS error

F ratio

Visualize

Contrast

Post-Hoc

Effect size

ANOVA factorial repeated

Factorial repeated measures ANOVA

Assumptions

Example

Data

Mixed design ANOVA

Mixed design

Assumptions

Example

Data

End

Contact

ANOVA
One-way repeated