ANOVA

Independent factorial

Klinkenberg

University of Amsterdam

13 oct 2022

Independent factorial ANOVA

Two or more independent variables with two or more categories. One dependent variable.

Independent factorial ANOVA

The independent factorial ANOVA analyses the variance of multiple independent variables (Factors) with two or more categories.

Effects and interactions:

1 dependent/outcome variable
2 or more independent/predictor variables
- 2 or more cat./levels

Assumptions

Continuous variable
Random sample
Normaly distributed
- Shapiro-Wilk test
Equal variance within groups
- Levene’s test

Formulas

Variance	Sum of squares	df	Mean squares	F-ratio
Model	\(\text{SS}_{\text{model}} = \sum{n_k(\bar{X}_k-\bar{X})^2}\)	\(k_{model}-1\)	\(\frac{\text{SS}_{\text{model}}}{\text{df}_{\text{model}}}\)	\(\frac{\text{MS}_{\text{model}}}{\text{MS}_{\text{error}}}\)
\(\hspace{2ex}A\)	\(\text{SS}_{\text{A}} = \sum{n_k(\bar{X}_k-\bar{X})^2}\)	\(k_A-1\)	\(\frac{\text{SS}_{\text{A}}}{\text{df}_{\text{A}}}\)	\(\frac{\text{MS}_{\text{A}}}{\text{MS}_{\text{error}}}\)
\(\hspace{2ex}B\)	\(\text{SS}_{\text{B}} = \sum{n_k(\bar{X}_k-\bar{X})^2}\)	\(k_B-1\)	\(\frac{\text{SS}_{\text{B}}}{\text{df}_{\text{B}}}\)	\(\frac{\text{MS}_{\text{B}}}{\text{MS}_{\text{error}}}\)
\(\hspace{2ex}AB\)	\(\text{SS}_{A \times B} = \text{SS}_{\text{model}} - \text{SS}_{\text{A}} - \text{SS}_{\text{B}}\)	\(df_A \times df_B\)	\(\frac{\text{SS}_{\text{AB}}}{\text{df}_{\text{AB}}}\)	\(\frac{\text{MS}_{\text{AB}}}{\text{MS}_{\text{error}}}\)
Error	\(\text{SS}_{\text{error}} = \sum{s_k^2(n_k-1)}\)	\(N-k_{model}\)	\(\frac{\text{SS}_{\text{error}}}{\text{df}_{\text{error}}}\)
Total	\(\text{SS}_{\text{total}} = \text{SS}_{\text{model}} + \text{SS}_{\text{error}}\)	\(N-1\)	\(\frac{\text{SS}_{\text{total}}}{\text{df}_{\text{total}}}\)

Example

In this example we will look at the amount of accidents in a car driving simulator while subjects where given varying doses of speed and alcohol.

Dependent variable
- Accidents
Independent variables
- Speed
  - None
  - Small
  - Large
- Alcohol
  - None
  - Small
  - Large

person	alcohol	speed	accidents
1	1	1	0
2	1	2	2
3	1	3	4
4	2	1	6
5	2	2	8
6	2	3	10
7	3	1	12
8	3	2	14
9	3	3	16

Data

SS model

Variance	Sum of squares	df	Mean squares	F-ratio
Model	\(\text{SS}_{\text{model}} = \sum{n_k(\bar{X}_k-\bar{X})^2}\)	\(k_{model}-1\)	\(\frac{\text{SS}_{\text{model}}}{\text{df}_{\text{model}}}\)	\(\frac{\text{MS}_{\text{model}}}{\text{MS}_{\text{error}}}\)

  speed alcohol accidents  n
1  much    much    7.5720 20
2  none    much    5.2970 20
3  some    much    6.5125 20
4  much    none    3.8880 20
5  none    none    2.1060 20
6  some    none    2.9445 20
7  much    some    5.5790 20
8  none    some    3.4435 20
9  some    some    4.7625 20

SS.model <- sum((exp.accidents - mean(data$accidents))^2); SS.model

[1] 494.2205

m.k1 = mean(subset(data, speed == "none" & alcohol == "none", select = "accidents")$accidents)
m.k2 = mean(subset(data, speed == "none" & alcohol == "some", select = "accidents")$accidents)
m.k3 = mean(subset(data, speed == "none" & alcohol == "much", select = "accidents")$accidents)
m.k4 = mean(subset(data, speed == "some" & alcohol == "none", select = "accidents")$accidents)
m.k5 = mean(subset(data, speed == "some" & alcohol == "some", select = "accidents")$accidents)
m.k6 = mean(subset(data, speed == "some" & alcohol == "much", select = "accidents")$accidents)
m.k7 = mean(subset(data, speed == "much" & alcohol == "none", select = "accidents")$accidents)
m.k8 = mean(subset(data, speed == "much" & alcohol == "some", select = "accidents")$accidents)
m.k9 = mean(subset(data, speed == "much" & alcohol == "much", select = "accidents")$accidents)

n.k1 = n.k2 = n.k3 = n.k4 = n.k5 = n.k6 = n.k7 = n.k8 = n.k9 = 20

ss.m.k1 = n.k1 * (m.k1 - mean(accidents))^2
ss.m.k2 = n.k2 * (m.k2 - mean(accidents))^2
ss.m.k3 = n.k3 * (m.k3 - mean(accidents))^2
ss.m.k4 = n.k4 * (m.k4 - mean(accidents))^2
ss.m.k5 = n.k5 * (m.k5 - mean(accidents))^2
ss.m.k6 = n.k6 * (m.k6 - mean(accidents))^2
ss.m.k7 = n.k7 * (m.k7 - mean(accidents))^2
ss.m.k8 = n.k8 * (m.k8 - mean(accidents))^2
ss.m.k9 = n.k9 * (m.k9 - mean(accidents))^2

ss.model = sum(ss.m.k1,ss.m.k2,ss.m.k3,ss.m.k4,ss.m.k5,ss.m.k6,ss.m.k7,ss.m.k8,ss.m.k9)
ss.model

[1] 494.2205

SS model visual

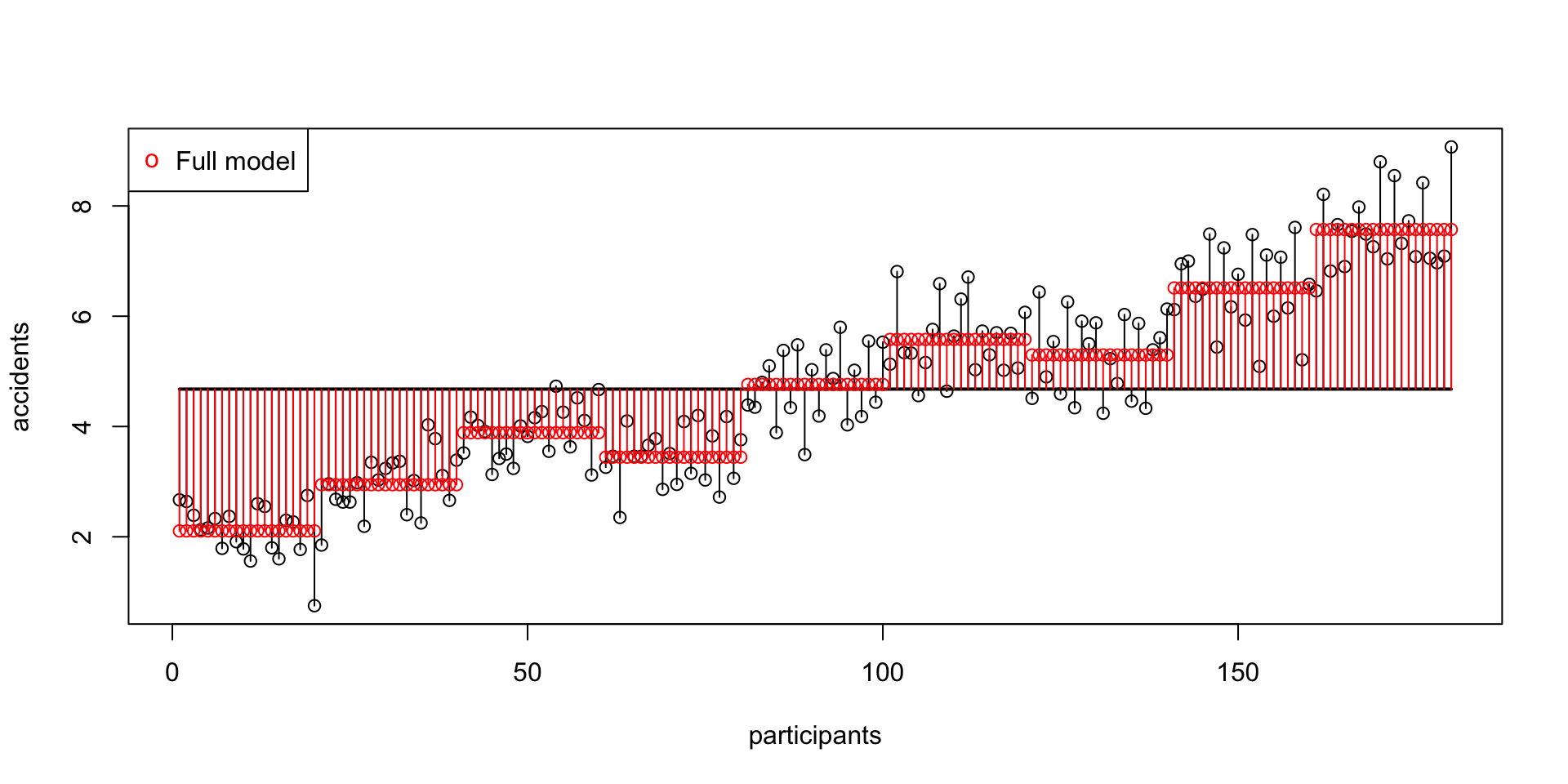
SS error

Variance	Sum of squares	df	Mean squares	F-ratio
Error	\(\text{SS}_{\text{error}} = \sum{s_k^2(n_k-1)}\)	\(N-k\)	\(\frac{\text{SS}_{\text{error}}}{\text{df}_{\text{error}}}\)

v.k1 = var(subset(data, speed == "none" & alcohol == "none", select = "accidents")$accidents)
v.k2 = var(subset(data, speed == "none" & alcohol == "some", select = "accidents")$accidents)
v.k3 = var(subset(data, speed == "none" & alcohol == "much", select = "accidents")$accidents)
v.k4 = var(subset(data, speed == "some" & alcohol == "none", select = "accidents")$accidents)
v.k5 = var(subset(data, speed == "some" & alcohol == "some", select = "accidents")$accidents)
v.k6 = var(subset(data, speed == "some" & alcohol == "much", select = "accidents")$accidents)
v.k7 = var(subset(data, speed == "much" & alcohol == "none", select = "accidents")$accidents)
v.k8 = var(subset(data, speed == "much" & alcohol == "some", select = "accidents")$accidents)
v.k9 = var(subset(data, speed == "much" & alcohol == "much", select = "accidents")$accidents)

ss.e.k1 = v.k1 * (n.k1 - 1)
ss.e.k2 = v.k2 * (n.k2 - 1)
ss.e.k3 = v.k3 * (n.k3 - 1)
ss.e.k4 = v.k4 * (n.k4 - 1)
ss.e.k5 = v.k5 * (n.k5 - 1)
ss.e.k6 = v.k6 * (n.k6 - 1)
ss.e.k7 = v.k7 * (n.k7 - 1)
ss.e.k8 = v.k8 * (n.k8 - 1)
ss.e.k9 = v.k9 * (n.k9 - 1)

ss.error = sum(ss.e.k1,ss.e.k2,ss.e.k3,ss.e.k4,ss.e.k5,ss.e.k6,ss.e.k7,ss.e.k8,ss.e.k9)
ss.error

[1] 66.34642

SS error visual

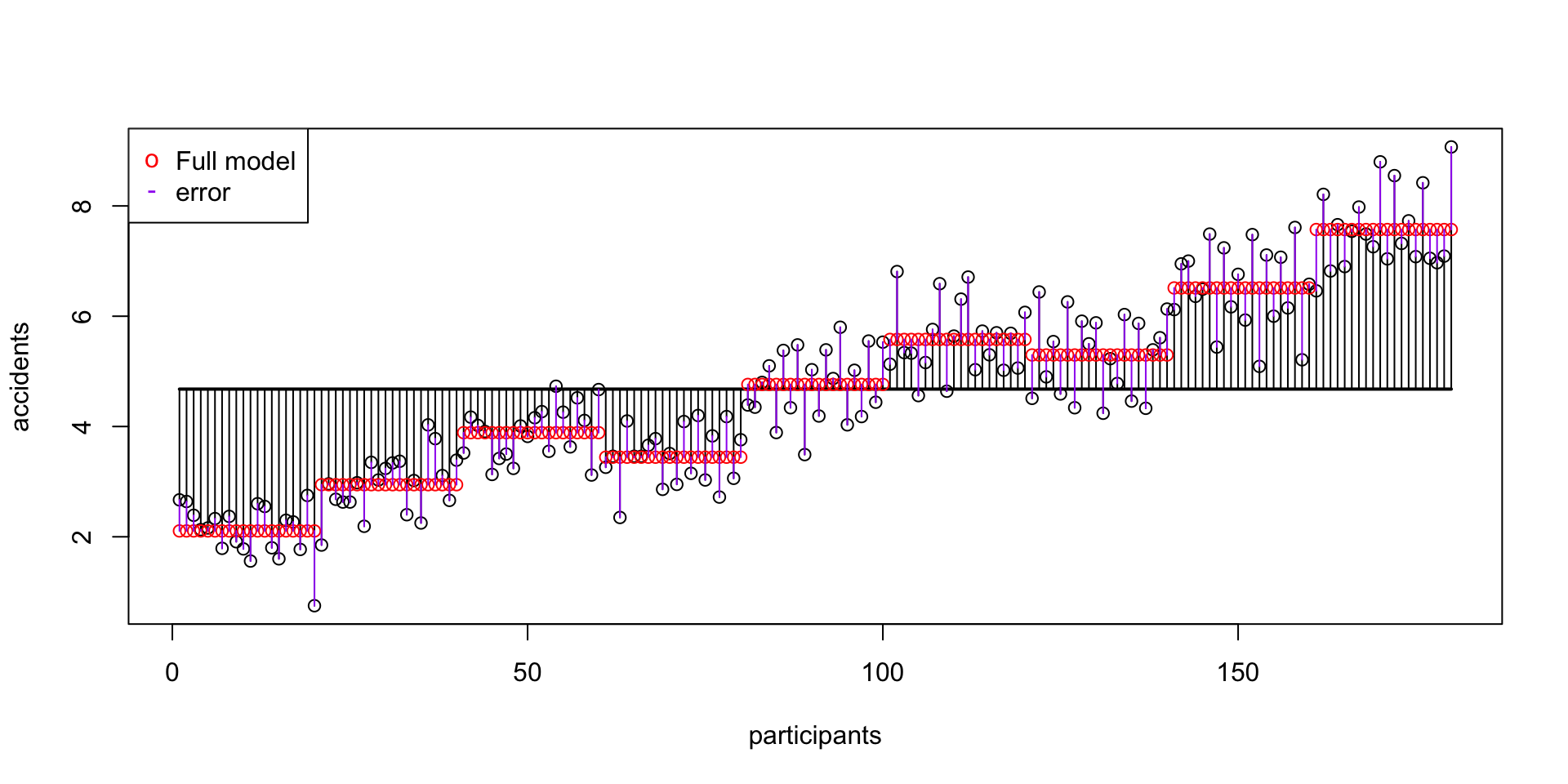
SS A Speed

Variance	Sum of squares	df	Mean squares	F-ratio
\(\hspace{2ex}A\)	\(\text{SS}_{\text{A}} = \sum{n_k(\bar{X}_k-\bar{X})^2}\)	\(k_A-1\)	\(\frac{\text{SS}_{\text{A}}}{\text{df}_{\text{A}}}\)	\(\frac{\text{MS}_{\text{A}}}{\text{MS}_{\text{error}}}\)

m.s1 = mean(subset(data, speed == "none", select = "accidents")$accidents)
m.s2 = mean(subset(data, speed == "some", select = "accidents")$accidents)
m.s3 = mean(subset(data, speed == "much", select = "accidents")$accidents)

n.s1 = n.s2 = n.s3 = 60

ss.s1 = n.s1 * (m.s1 - mean(accidents))^2
ss.s2 = n.s2 * (m.s2 - mean(accidents))^2
ss.s3 = n.s3 * (m.s3 - mean(accidents))^2

ss.speed = sum(ss.s1,ss.s2,ss.s3)
ss.speed

[1] 128.1639

SS A Speed Visual

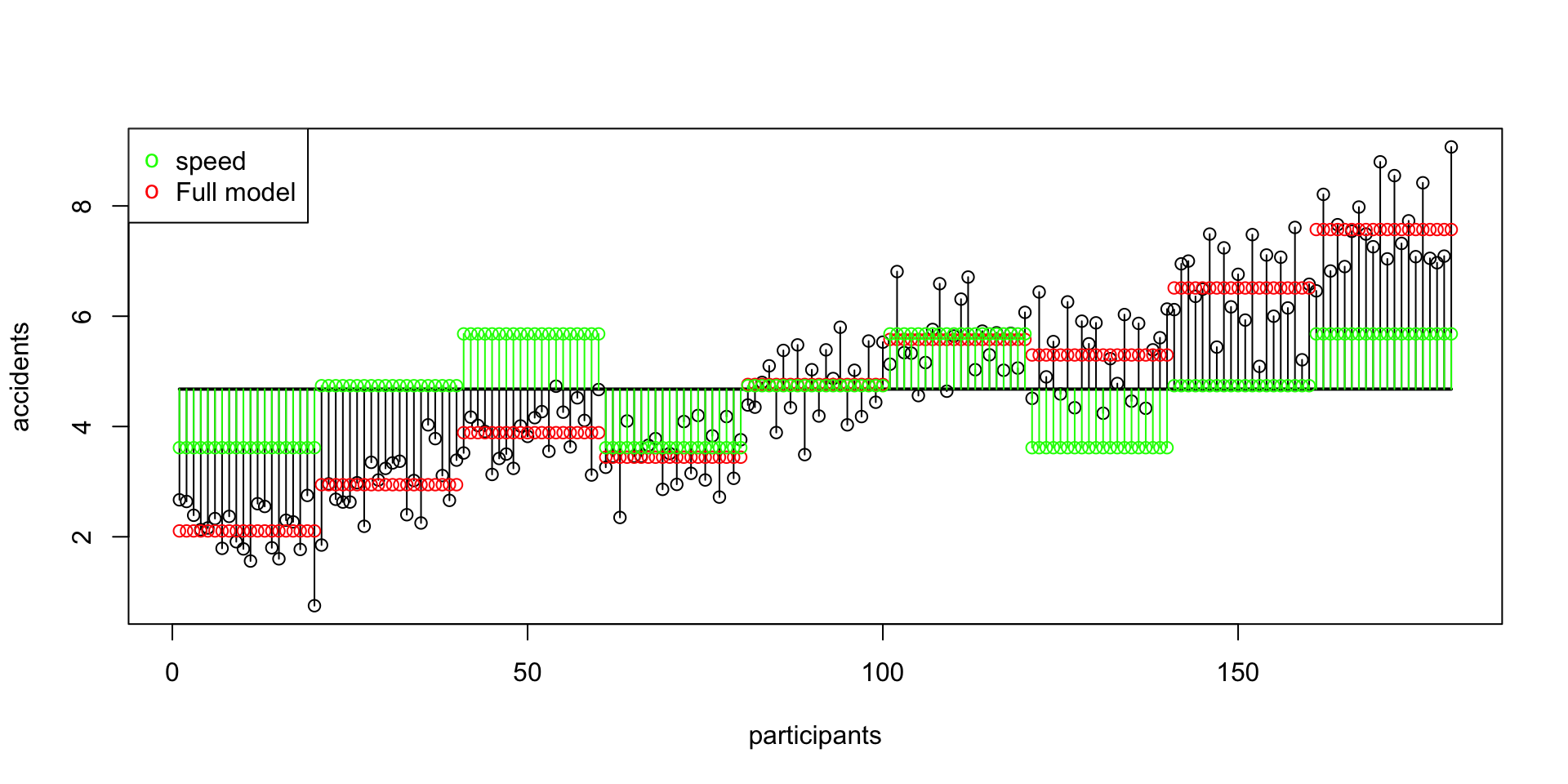
SS B Alcohol

Variance	Sum of squares	df	Mean squares	F-ratio
\(\hspace{2ex}B\)	\(\text{SS}_{\text{B}} = \sum{n_k(\bar{X}_k-\bar{X})^2}\)	\(k_B-1\)	\(\frac{\text{SS}_{\text{B}}}{\text{df}_{\text{B}}}\)	\(\frac{\text{MS}_{\text{B}}}{\text{MS}_{\text{error}}}\)

ss.a1 = n.a1 * (m.a1 - mean(accidents))^2 
ss.a2 = n.a2 * (m.a2 - mean(accidents))^2 
ss.a3 = n.a3 * (m.a3 - mean(accidents))^2 

ss.alcohol = sum(ss.a1,ss.a2,ss.a3)
ss.alcohol

[1] 364.1458

SS B Alcohol Visual

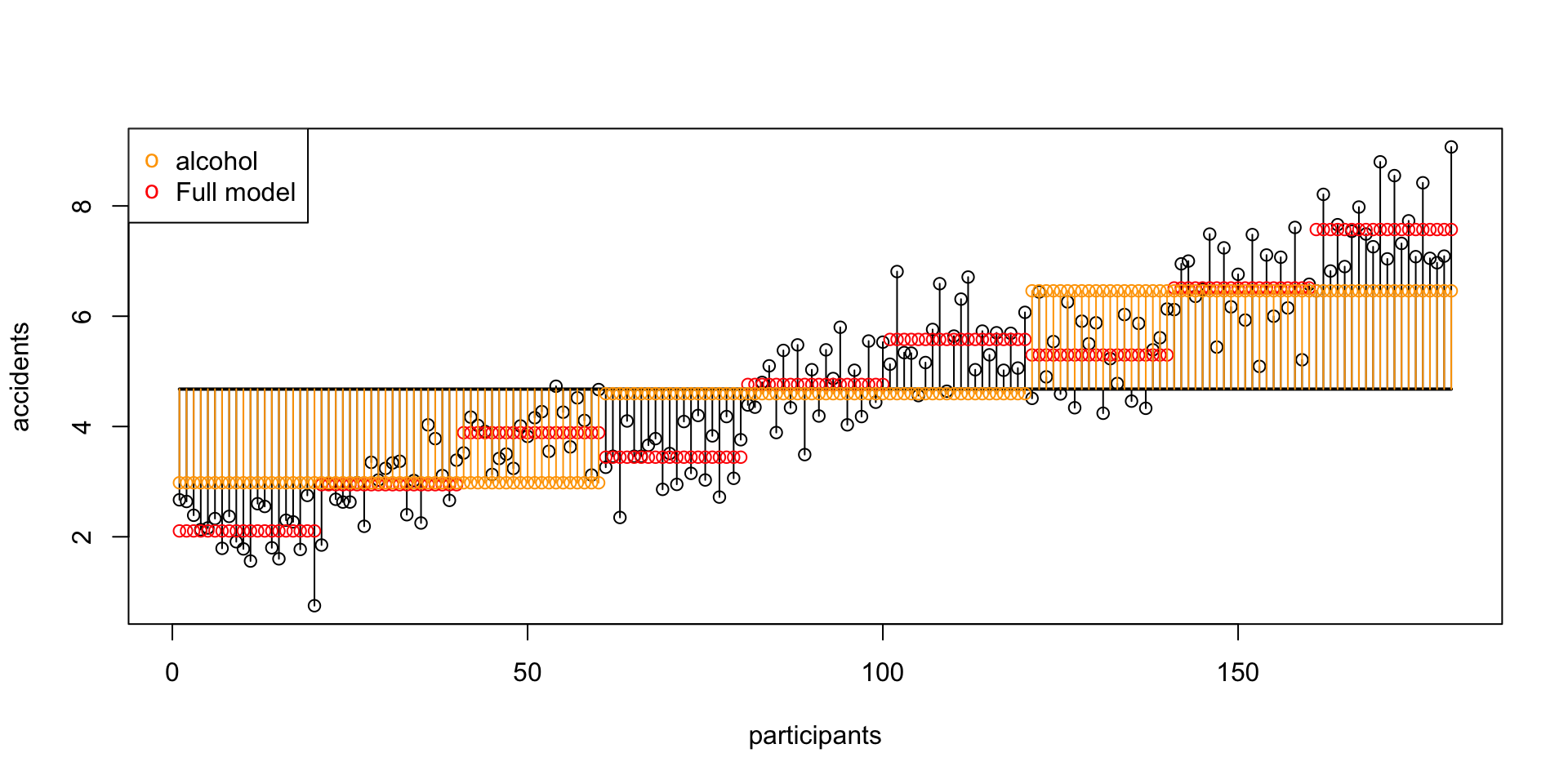
SS AB Alcohol x Speed

Variance	Sum of squares	df	Mean squares	F-ratio
\(\hspace{2ex}AB\)	\(\text{SS}_{A \times B} = \text{SS}_{\text{model}} - \text{SS}_{\text{A}} - \text{SS}_{\text{B}}\)	\(df_A \times df_B\)	\(\frac{\text{SS}_{\text{AB}}}{\text{df}_{\text{AB}}}\)	\(\frac{\text{MS}_{\text{AB}}}{\text{MS}_{\text{error}}}\)

# Sums of squares for the interaction between speed and alcohol
ss.speed.alcohol <- ss.model - ss.speed - ss.alcohol
ss.speed.alcohol

[1] 1.910727

Mean Squares

Mean squares for:

Speed
Alcohol
Speed \(\times\) Alcohol

\[\begin{aligned} F_{Speed} &= \frac{{MS}_{Speed}}{{MS}_{error}} \\ F_{Alcohol} &= \frac{{MS}_{Alcohol}}{{MS}_{error}} \\ F_{Alcohol \times Speed} &= \frac{{MS}_{Alcohol \times Speed}}{{MS}_{error}} \\ \end{aligned}\]

Interaction

\[F_{Alcohol \times Speed}\]

N          = length(accidents)
k.speed    = 3
k.alcohol  = 3
k.model    = 9
df.speed   = k.speed   - 1
df.alcohol = k.alcohol - 1
df.speed.alcohol = df.speed * df.alcohol

ms.speed.alcohol = ss.speed.alcohol / df.speed.alcohol

df.error = N - k.model
ms.error = ss.error / df.error

\(P\)-value

F.speed.alcohol = ms.speed.alcohol / ms.error
F.speed.alcohol

[1] 1.231168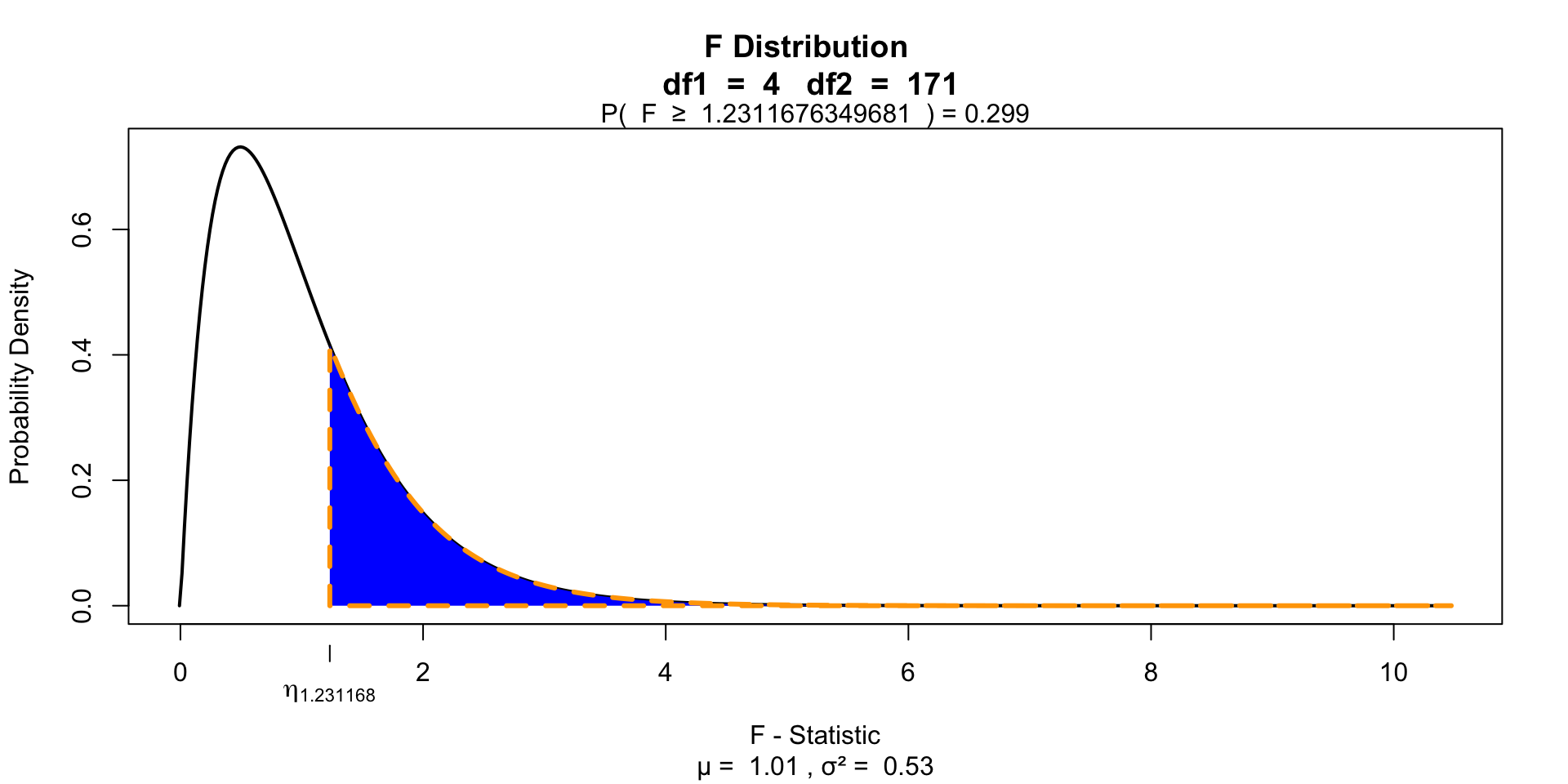

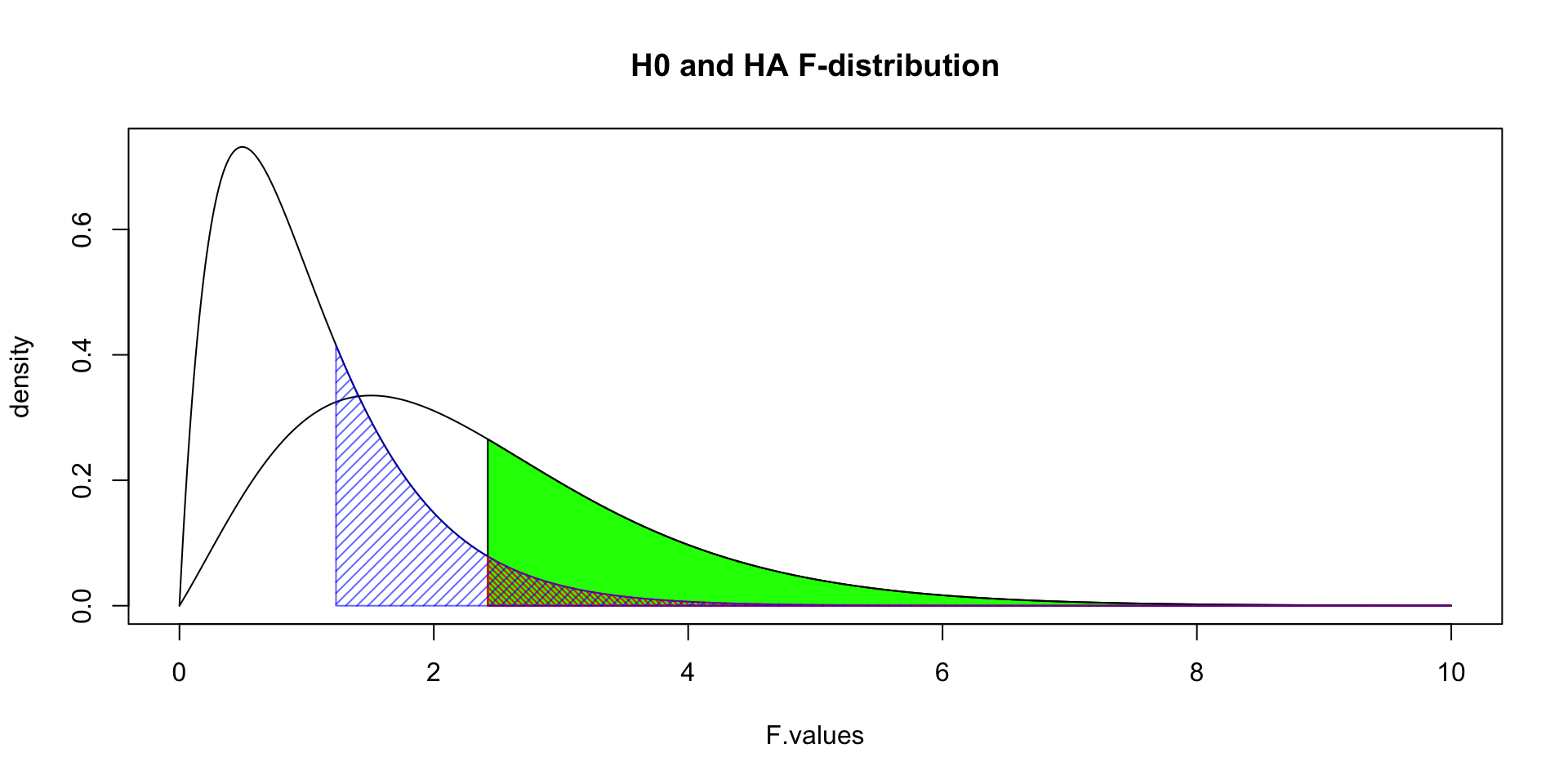
library(visualize)
visualize.f(F.speed.alcohol, df.speed.alcohol, df.error, section = "upper")

Contrast

Planned comparisons

Exploring differences of theoretical interest
Higher precision
Higher power

Post-Hoc

Unplanned comparisons

Exploring all possible differences
Adjust T value for inflated type 1 error

Effect size

General effect size measures

Amount of explained variance \(R^2\) also called eta squared \(\eta^2\).
Omega squared \(\omega^2\)

Effect sizes of contrasts or post-hoc comparisons

Cohen’s \(r\) gives the effect size for a specific comparison
- \(r_{Contrast} = \sqrt{\frac{t^2}{t^2+{df}}}\)

End

Contact