Probability Models

Klinkenberg

University of Amsterdam

2025-09-08

Why do we need them

Exact approach

Applicable

Exact probabilities can only be calculated for:

  • Discreet variables
  • Categorical variables

An exact approach lists and counts all possible combinations.

Coin values

Coin values for heads and tails.

\(\{1, 0\}\)

10 tosses

Toss1 Toss2 Toss3 Toss4 Toss5 Toss6 Toss7 Toss8 Toss9 Toss10
0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5
0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5
0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5
0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5
0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5
0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5
0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5
Toss1 Toss2 Toss3 Toss4 Toss5 Toss6 Toss7 Toss8 Toss9 Toss10 probability
0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.0009766
0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.0009766
0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.0009766
0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.0009766
0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.0009766
#Heads frequencies Probabilities
0 1 0.0009766
1 10 0.0097656
2 45 0.0439453
3 120 0.1171875
4 210 0.2050781
5 252 0.2460938
6 210 0.2050781
7 120 0.1171875
8 45 0.0439453
9 10 0.0097656
10 1 0.0009766

Calculate binomial probabilities

\[ {n\choose k}p^k(1-p)^{n-k}, \small {n\choose k} = \frac{n!}{k!(n-k)!} \]

n = 10   # Sample size
k = 0:10 # Discrete probability space
p = .5   # Probability of head
n k p n! k! (n-k)! (n over k) p^k (1-p)^(n-k) Binom Prob
10 0 0.5 3628800 1 3628800 1 1.0000000 0.0009766 0.0009766
10 1 0.5 3628800 1 362880 10 0.5000000 0.0019531 0.0097656
10 2 0.5 3628800 2 40320 45 0.2500000 0.0039063 0.0439453
10 3 0.5 3628800 6 5040 120 0.1250000 0.0078125 0.1171875
10 4 0.5 3628800 24 720 210 0.0625000 0.0156250 0.2050781
10 5 0.5 3628800 120 120 252 0.0312500 0.0312500 0.2460938
10 6 0.5 3628800 720 24 210 0.0156250 0.0625000 0.2050781
10 7 0.5 3628800 5040 6 120 0.0078125 0.1250000 0.1171875
10 8 0.5 3628800 40320 2 45 0.0039063 0.2500000 0.0439453
10 9 0.5 3628800 362880 1 10 0.0019531 0.5000000 0.0097656
10 10 0.5 3628800 3628800 1 1 0.0009766 1.0000000 0.0009766

Warning

Formula not exam material

Binomial distribution

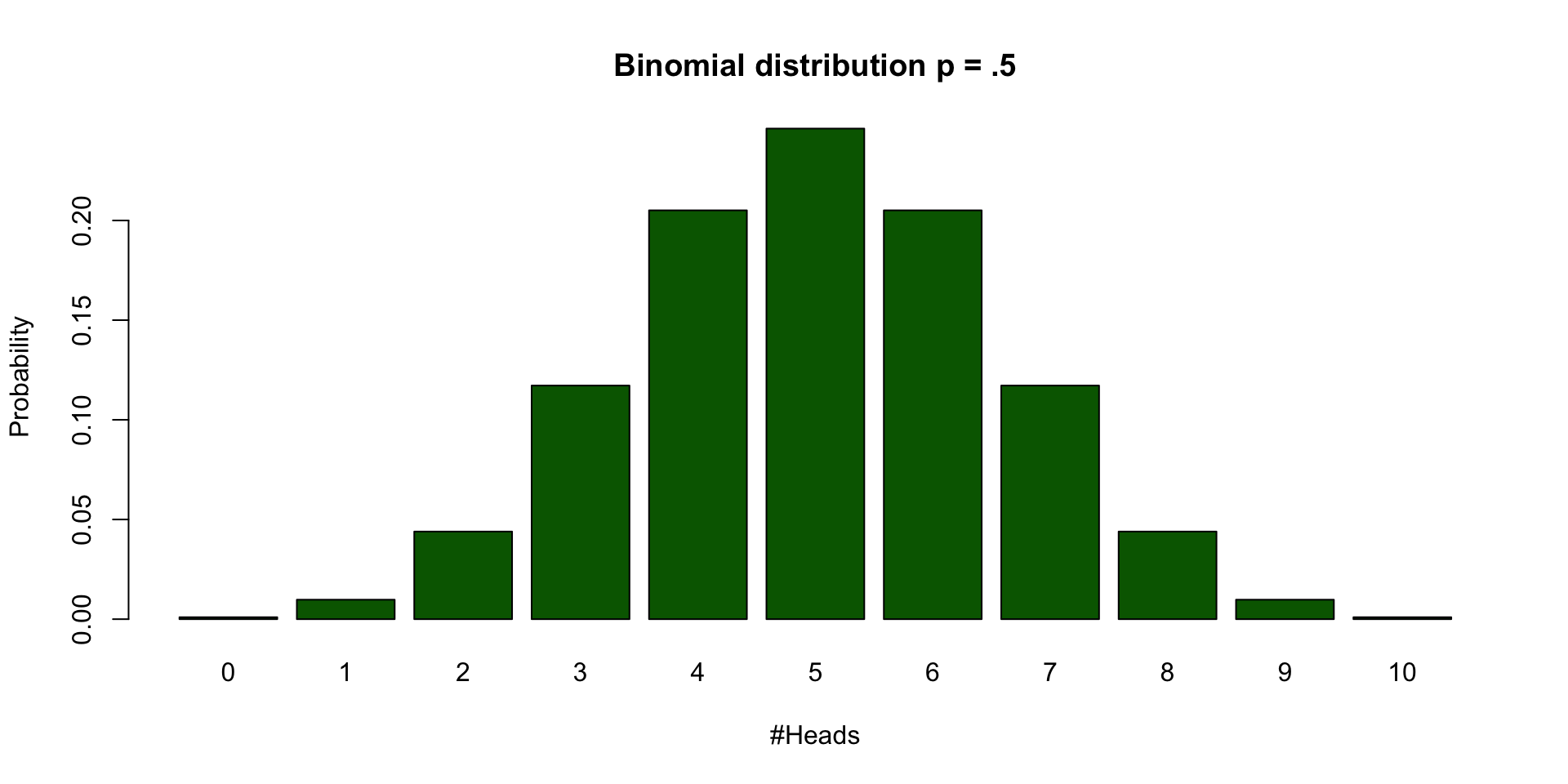
Bootstrapping

Sampling from your sample to approximate the sampling distribution.

My Coin tosses

my.tosses = c(0,0,1,0,0,0,0,0,1,0)

Sample from the sample

Sampling with replacement

sample(my.tosses, replace = TRUE)
 [1] 0 0 0 0 0 0 0 0 0 0
sample(my.tosses, replace = TRUE)
 [1] 1 0 0 0 0 0 0 1 0 0
sample(my.tosses, replace = TRUE)
 [1] 0 0 0 0 1 0 0 0 0 0
sample(my.tosses, replace = TRUE)
 [1] 0 0 0 0 1 1 0 0 0 0

Sampling from the sample

n.bootstrap.samples = 1000
n.heads = vector()

for (i in 1:n.bootstrap.samples) {
  bootstrap.sample <- sample(my.tosses, replace = TRUE)
  
  n.heads[i] <- sum(bootstrap.sample) 
}
0 0 3 2 0 3 3 2 3 6 5 2 4 1 3 2 4 2 2 5 1 1 1 2 0 2 3 3 2 2 3 0 1 2 5 4 0 2 1 2
4 3 0 2 3 2 2 4 2 0 4 3 3 3 3 2 0 1 4 2 2 1 3 2 1 1 0 0 1 2 2 4 1 3 1 0 4 2 1 2
0 3 1 2 2 0 1 5 3 1 1 0 1 5 3 0 2 1 1 2 2 1 4 3 1 2 0 2 2 2 3 3 2 3 0 1 3 3 1 3
2 3 2 2 1 3 1 1 2 3 1 1 1 2 0 5 4 2 2 3 1 2 1 2 0 1 2 3 2 2 2 3 3 3 1 2 1 4 3 4
1 2 0 4 0 4 2 2 0 1 4 1 1 3 2 4 1 2 2 1 2 3 3 1 2 1 2 0 1 2 1 2 2 2 3 3 1 2 3 2
2 1 1 2 1 1 1 1 2 3 1 1 2 2 2 0 3 2 4 1 4 1 2 1 1 2 2 3 3 1 2 1 1 0 1 1 2 2 0 0
3 2 3 1 0 0 2 2 4 5 3 2 2 1 0 3 0 1 3 3 3 0 1 2 2 2 2 3 3 3 1 1 2 3 2 2 3 1 4 0
0 3 2 4 4 3 1 3 4 1 6 2 2 1 0 3 1 1 3 3 1 2 1 2 1 3 2 3 1 1 3 4 2 2 3 1 2 2 2 0
2 2 3 2 2 3 3 2 1 2 1 1 0 2 1 0 4 2 2 2 1 2 1 3 1 1 1 4 3 5 2 4 1 1 2 3 2 2 2 2
2 3 4 1 1 2 1 2 3 3 3 2 1 1 1 1 3 1 1 1 1 0 2 1 2 4 4 5 1 1 3 4 2 2 3 2 3 2 2 2
2 0 0 3 3 0 2 1 2 2 2 2 1 2 4 3 1 1 2 3 4 1 0 2 0 2 2 4 1 3 2 5 3 3 1 4 2 0 1 2
4 5 3 3 3 1 2 2 3 2 2 1 4 3 1 0 3 1 1 2 2 1 4 0 3 4 3 1 2 1 1 0 3 3 2 0 1 4 2 3
4 2 3 0 4 2 3 1 1 0 4 1 3 2 2 1 3 0 2 1 3 2 3 4 2 3 3 4 0 2 1 1 2 2 4 3 1 3 2 1
2 1 1 0 4 1 2 1 1 5 3 2 4 2 2 1 1 1 3 2 2 3 1 3 1 1 3 1 4 1 1 1 1 2 2 1 3 3 2 3
1 2 5 5 2 5 2 3 1 1 1 3 3 1 2 4 1 1 4 3 1 4 1 1 3 1 0 2 2 0 1 1 0 1 1 2 4 2 1 4
2 1 1 2 2 3 3 1 3 3 1 3 2 3 2 2 4 1 2 4 2 3 1 1 2 4 0 0 3 0 2 0 4 0 0 1 1 1 1 1
2 1 1 2 4 3 4 3 2 3 0 1 1 1 2 1 4 2 1 1 1 2 3 2 0 0 0 4 3 2 1 1 5 1 0 1 1 5 3 4
0 2 0 4 4 4 1 4 3 1 1 2 4 2 0 0 5 1 1 1 1 1 2 2 2 2 2 0 2 3 1 3 2 2 1 4 2 2 0 1
0 3 2 0 1 1 3 0 1 2 2 2 1 3 3 3 2 0 1 4 1 3 2 3 1 2 0 1 3 2 1 2 2 3 0 4 2 6 3 1
1 2 1 1 2 1 3 1 5 2 1 2 2 3 2 4 2 2 4 1 3 2 2 3 1 2 1 2 7 3 1 3 2 1 2 3 3 1 2 4
2 3 1 2 1 2 1 4 3 3 2 1 3 4 0 0 0 0 4 2 2 2 5 3 0 3 6 2 2 1 2 2 4 3 3 0 1 1 0 3
0 1 1 2 2 2 2 0 3 2 1 4 0 4 3 1 3 2 1 3 3 0 2 3 0 2 1 2 2 3 2 1 1 2 2 2 2 1 3 2
2 4 2 2 0 0 5 3 0 2 4 0 3 2 1 1 4 1 1 1 4 1 2 0 3 3 2 2 4 3 1 1 0 2 2 0 4 2 0 1
1 1 2 1 4 4 2 2 0 2 0 4 2 0 1 2 2 4 3 1 3 4 0 2 2 1 3 2 3 3 0 2 2 1 0 2 3 2 1 1
2 4 4 2 2 2 4 2 2 1 3 2 2 1 4 2 2 4 5 3 4 2 2 1 3 3 3 5 4 3 3 3 2 6 3 3 2 1 3 1

Frequencies

Frequencies for number of heads per sample.

0 1 2 3 4 5 6 7 8 9 10
Freq 107 265 304 196 99 23 5 1 0 0 0

Bootstrapped sampling distribution

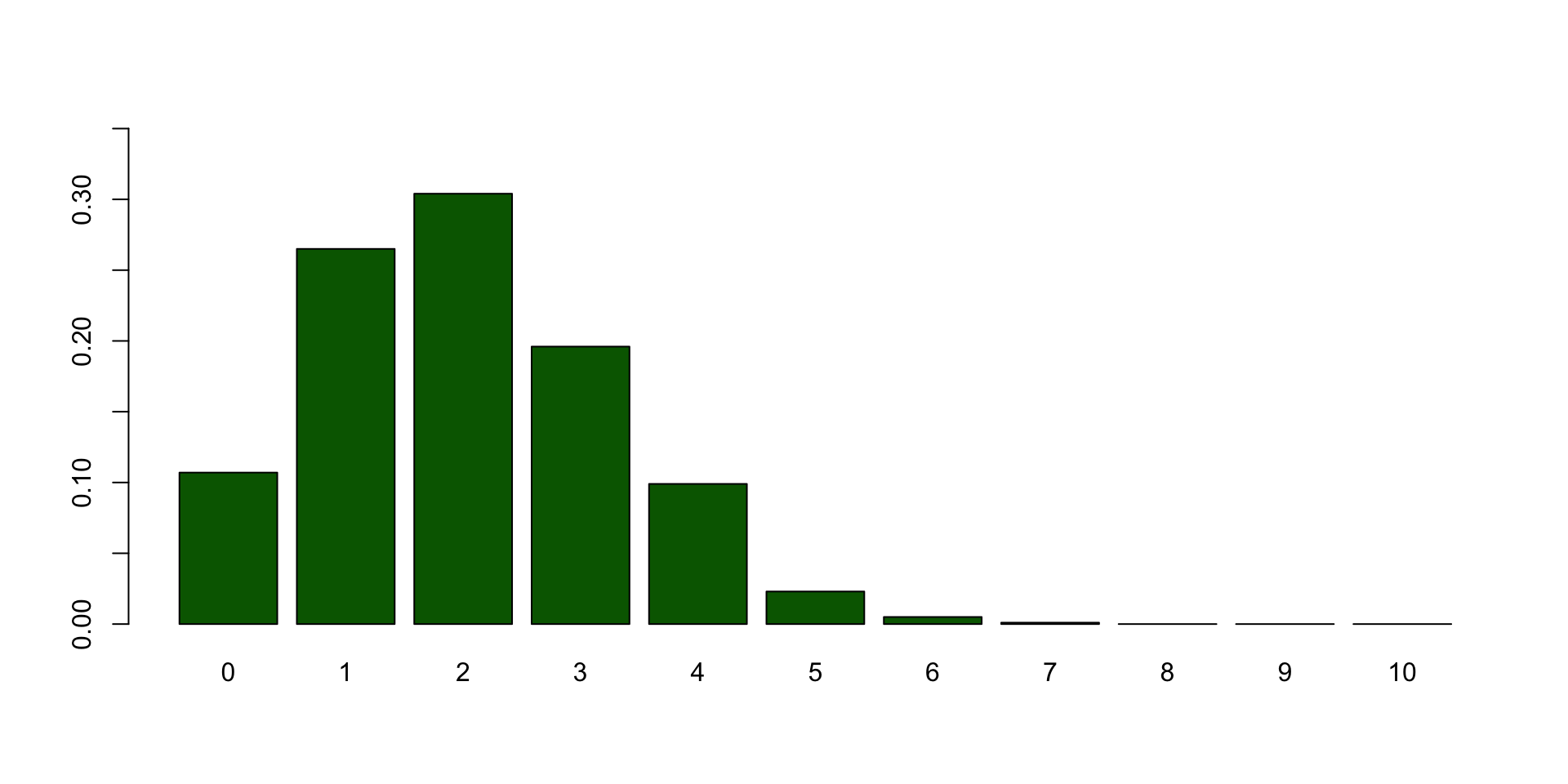
Theoretical Approximations

Continuous Probability distirbutions

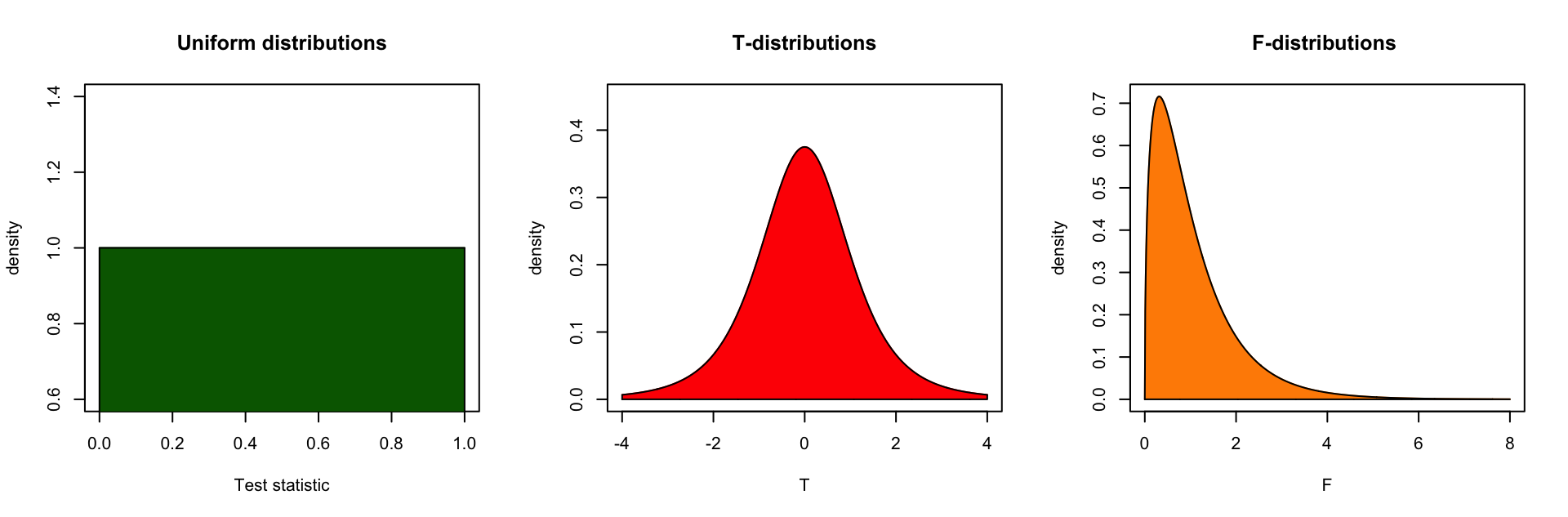
For all continuous probability distributions:

  • Total area is always 1
  • The probability of one specific test statistic is 0
  • x-axis represents the test statistic
  • y-axis represents the probability density

T-distribution

Gosset

William Sealy Gosset (aka Student) in 1908 (age 32)

In probability and statistics, Student’s t-distribution (or simply the t-distribution) is any member of a family of continuous probability distributions that arises when estimating the mean of a normally distributed population in situations where the sample size is small and population standard deviation is unknown.

In the English-language literature it takes its name from William Sealy Gosset’s 1908 paper in Biometrika under the pseudonym “Student”. Gosset worked at the Guinness Brewery in Dublin, Ireland, and was interested in the problems of small samples, for example the chemical properties of barley where sample sizes might be as low as 3 (Wikipedia, 2024).

Population distribution

layout(matrix(c(2:6,1,1,7:8,1,1,9:13), 4, 4))

n  = 56    # Sample size
df = n - 1 # Degrees of freedom

mu    = 120
sigma = 15

IQ = seq(mu-45, mu+45, 1)

par(mar=c(4,2,2,0))  
plot(IQ, dnorm(IQ, mean = mu, sd = sigma), type='l', col="red", main = "Population Distribution")

n.samples = 12

for(i in 1:n.samples) {
  
  par(mar=c(2,2,2,0))  
  hist(rnorm(n, mu, sigma), main="Sample Distribution", cex.axis=.5, col="beige", cex.main = .75)
  
}

Population distribution

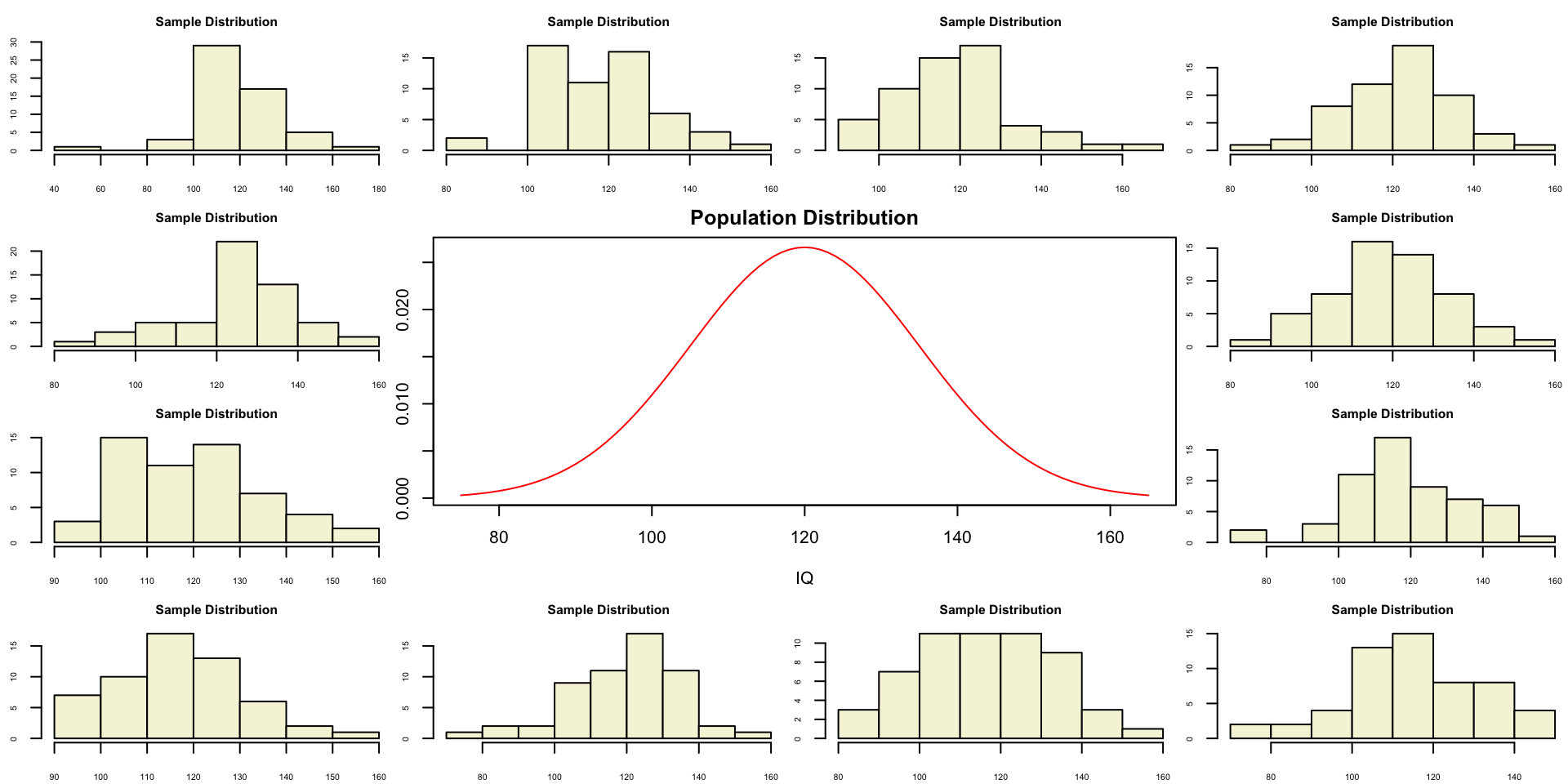
One sample

Let’s take a larger sample from our normal population.

x = rnorm(n, mu, sigma); x
 [1] 125.38159 131.87150  97.91258 106.65761 128.79834 130.37589 104.12035
 [8] 137.92415 135.05426 136.38486 143.56131 110.19591 111.06758  81.15490
[15] 124.67001 137.63382 115.79382 131.16588 122.68704 124.44491 121.53545
[22] 134.25584 121.45674 132.00408 139.55906  98.17081 121.98904 122.04234
[29] 118.85838 136.76335 142.98176 107.43160 115.22124 137.70291 131.19283
[36] 105.44568 131.72974 107.19139 130.45036 116.90866 115.49826 123.98368
[43] 120.42300 114.66301 114.37692 116.56588 112.17237 102.97537 130.09115
[50] 137.89815 104.97558 150.87956  95.52687 143.39545 114.49853 121.09488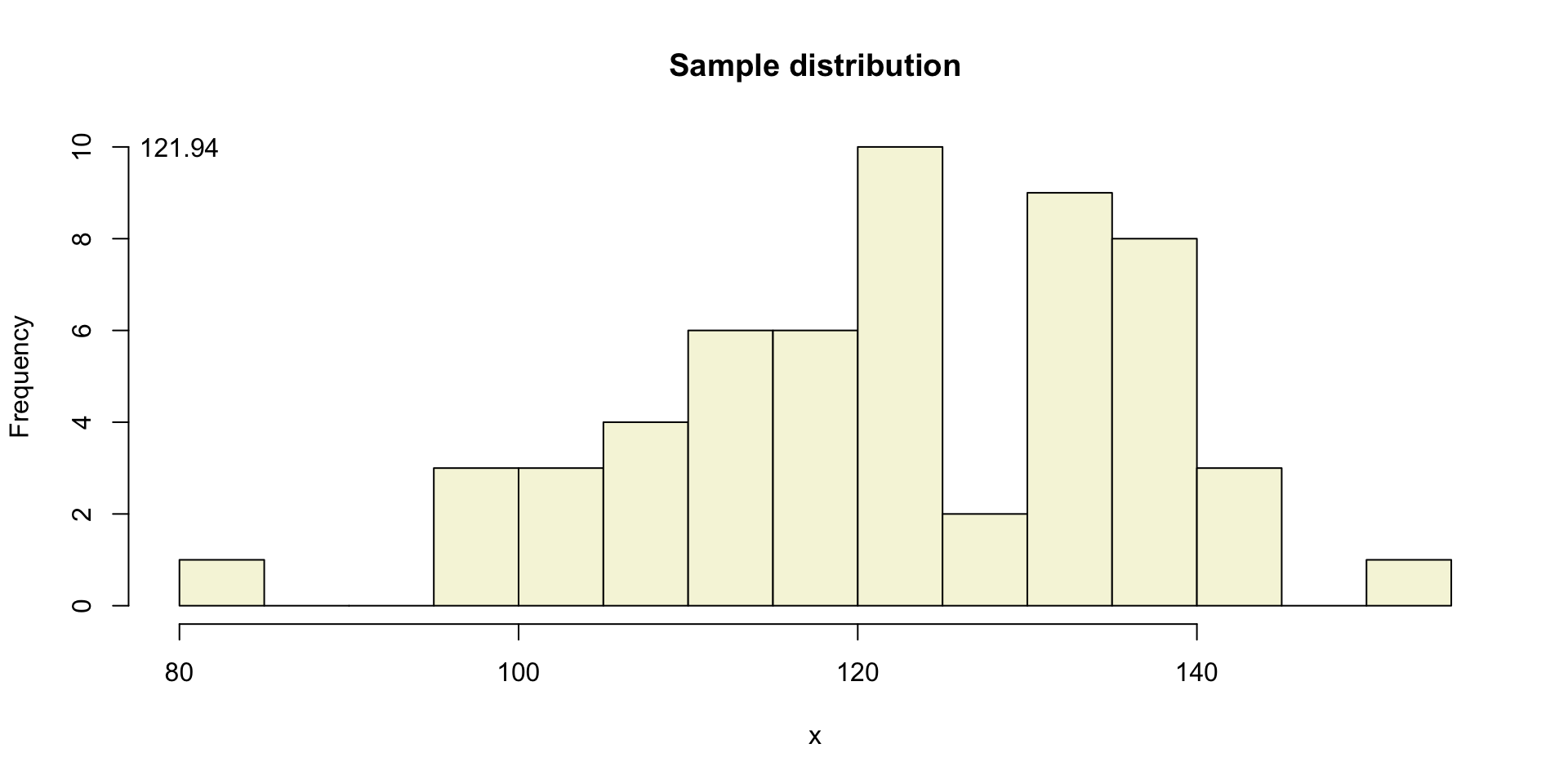

More samples

let’s take more samples.

n.samples     = 1000
mean.x.values = vector()
sd.x.values   = vector()
se.x.values   = vector()

for(i in 1:n.samples) {
  x = rnorm(n, mu, sigma)
  mean.x.values[i] = mean(x)
  se.x.values[i]   = (sd(x) / sqrt(n))
  sd.x.values[i]   = sd(x)
}

Mean and SE for all samples

     mean.x.values se.x.values
[1,]      118.9136    2.025850
[2,]      118.6910    1.900806
[3,]      121.9166    2.080805
[4,]      119.9850    2.336038
[5,]      119.8122    1.781885
[6,]      121.7780    2.006616
        mean.x.values se.x.values
 [995,]      118.6369    2.270611
 [996,]      120.8203    1.729008
 [997,]      122.0699    1.850029
 [998,]      122.4615    2.048059
 [999,]      119.8978    2.042032
[1000,]      121.0900    1.709775

Sampling distribution

of the mean

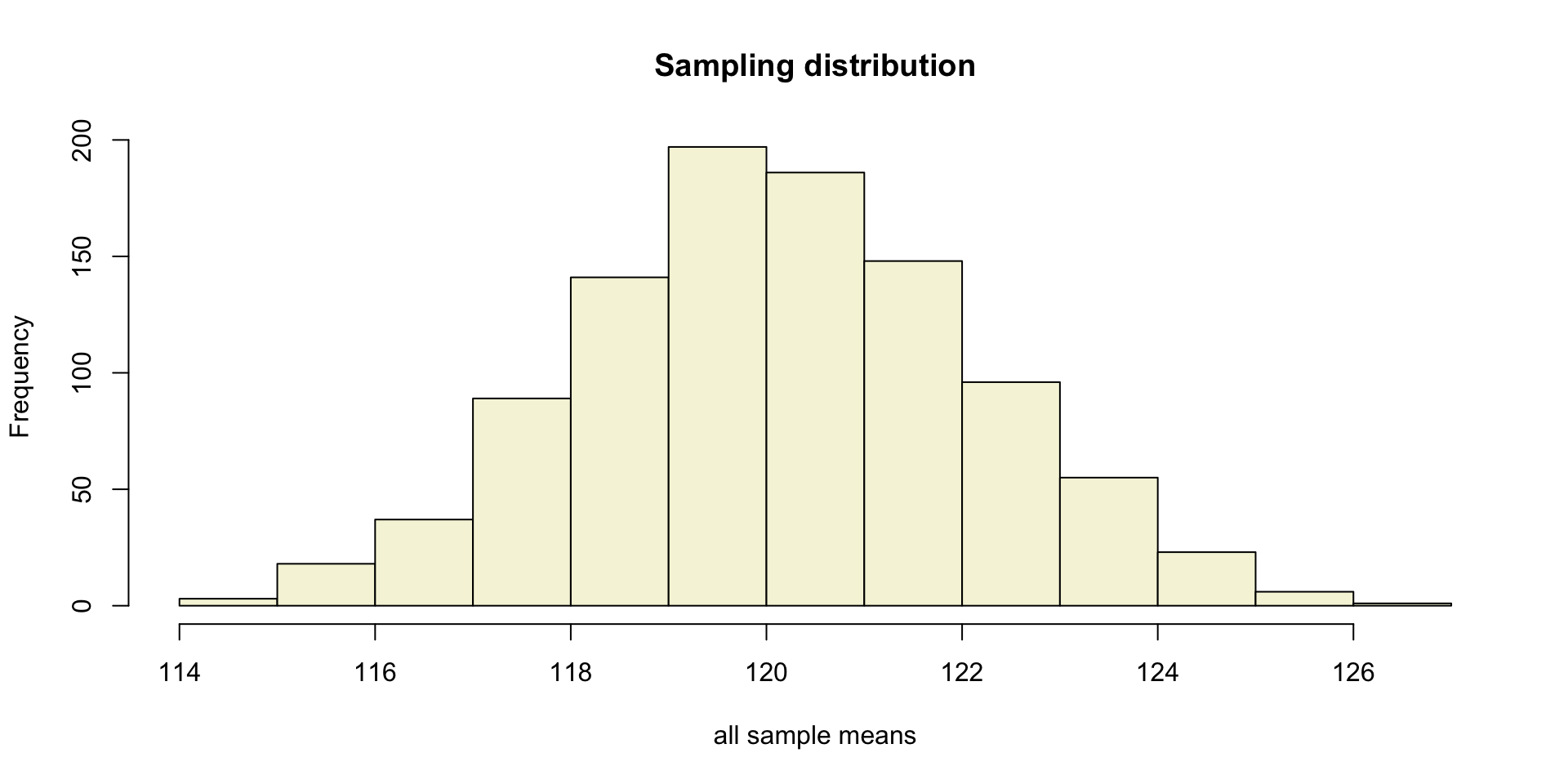
T-statistic

\[T_{n-1} = \frac{\bar{x}-\mu}{SE_x} = \frac{\bar{x}-\mu}{s_x / \sqrt{n}}\]

So the t-statistic represents the deviation of the sample mean \(\bar{x}\) from the population mean \(\mu\), considering the sample size, expressed as the degrees of freedom \(df = n - 1\)

T-value

\[T_{n-1} = \frac{\bar{x}-\mu}{SE_x} = \frac{\bar{x}-\mu}{s_x / \sqrt{n}}\]

t = (mean(x) - mu) / (sd(x) / sqrt(n))
t
[1] 0.6374982

Calculate t-values

\[T_{n-1} = \frac{\bar{x}-\mu}{SE_x} = \frac{\bar{x}-\mu}{s_x / \sqrt{n}}\]

t.values = (mean.x.values - mu) / se.x.values
        mean.x.values  mu se.x.values    t.values
 [995,]      118.6369 120    2.270611 -0.60033932
 [996,]      120.8203 120    1.729008  0.47445351
 [997,]      122.0699 120    1.850029  1.11885233
 [998,]      122.4615 120    2.048059  1.20187523
 [999,]      119.8978 120    2.042032 -0.05004259
[1000,]      121.0900 120    1.709775  0.63749824

Sampling distribution t-values

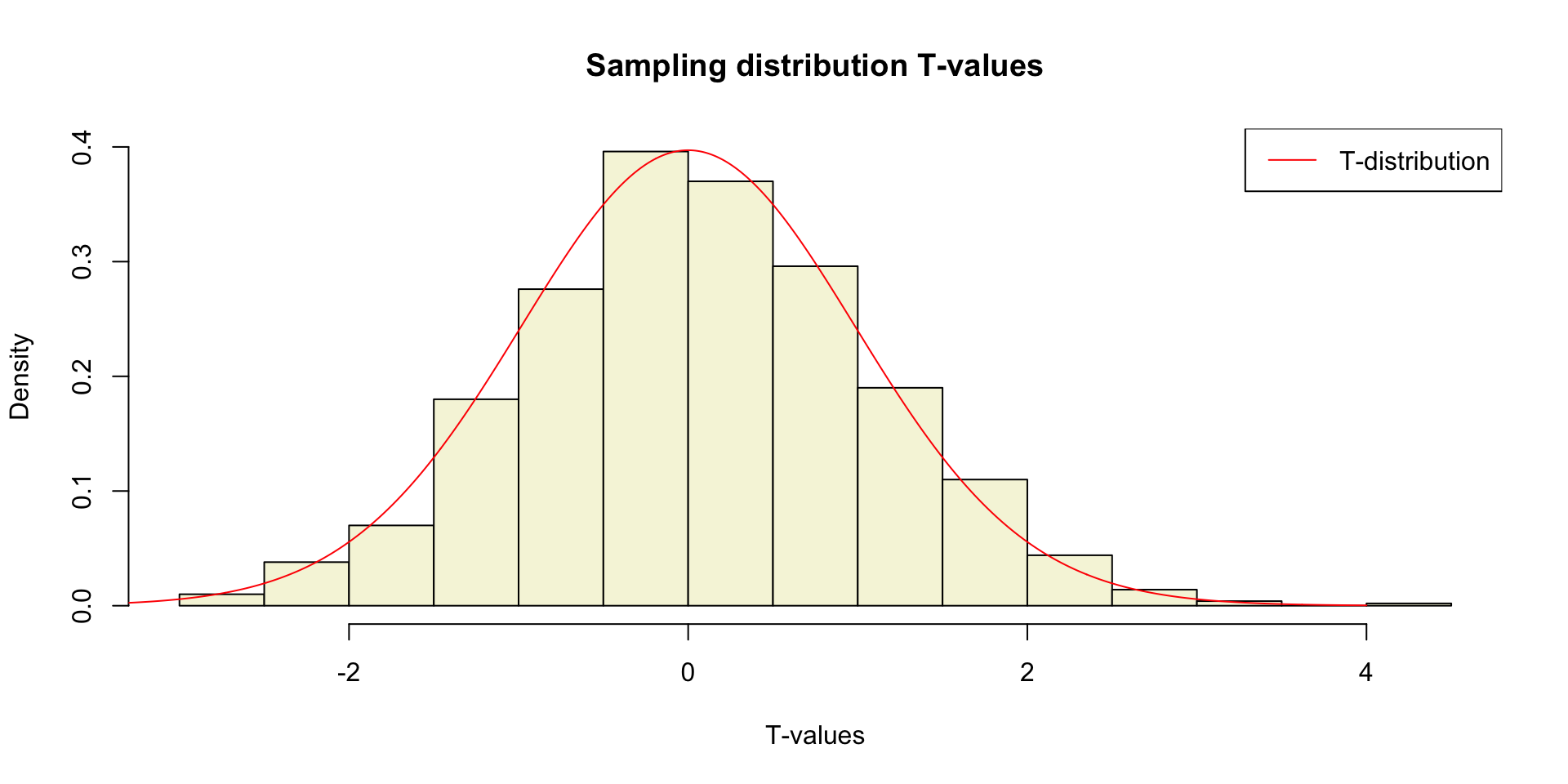
The t-distribution approximates the sampling distribution, hence the name theoretical approximation.

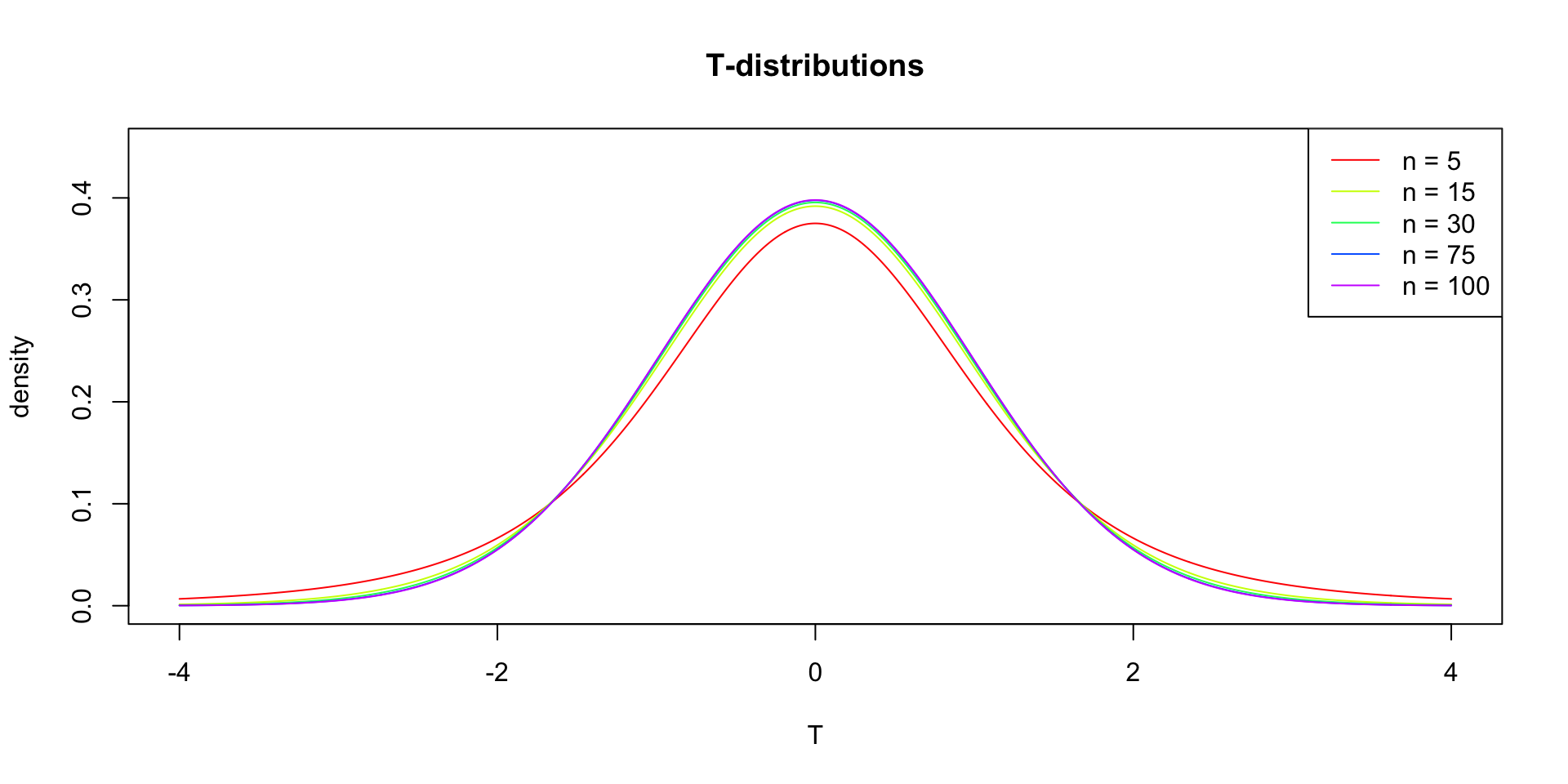
T-distribution

So if the population is normaly distributed (assumption of normality) the t-distribution represents the deviation of sample means from the population mean (\(\mu\)), given a certain sample size (\(df = n - 1\)).

The t-distibution therefore is different for different sample sizes and converges to a standard normal distribution if sample size is large enough.

The t-distribution is defined by the probability density function (PDF):

\[\textstyle\frac{\Gamma \left(\frac{\nu+1}{2} \right)} {\sqrt{\nu\pi}\,\Gamma \left(\frac{\nu}{2} \right)} \left(1+\frac{x^2}{\nu} \right)^{-\frac{\nu+1}{2}}\!\]

where \(\nu\) is the number of degrees of freedom and \(\Gamma\) is the gamma function (Wikipedia, 2024).

Warning

Formula not exam material

End

Contact

CC BY-NC-SA 4.0

References

Wikipedia. (2024). Student’s t-distribution — Wikipedia, the free encyclopedia. http://en.wikipedia.org/w/index.php?title=Student's%20t-distribution&oldid=1202978121.
  • Distribution illustration generated with DALL-E by OpenAI