Mediation

Klinkenberg

University of Amsterdam

2024-10-14

Mediation

In statistics, a mediation model is one that seeks to identify and explain the mechanism or process that underlies an observed relationship between an independent variable and a dependent variable via the inclusion of a third hypothetical variable, known as a mediator variable (also a mediating variable, intermediary variable, or intervening variable) (Wikipedia, 2024).

Causality

Mediation does not imply causation!

Criteria for causal relations

All requirements need to be met:

1. Correlation
2. Time order
3. No spurious (false) correlation
4. No common cause confounder

Example

Does the speed of recovery after sickness improve with the use of alternative medicine or is this effect mediated by a healthy lifestyle?

Photo by Pixabay from Pexels

Mediaton paths

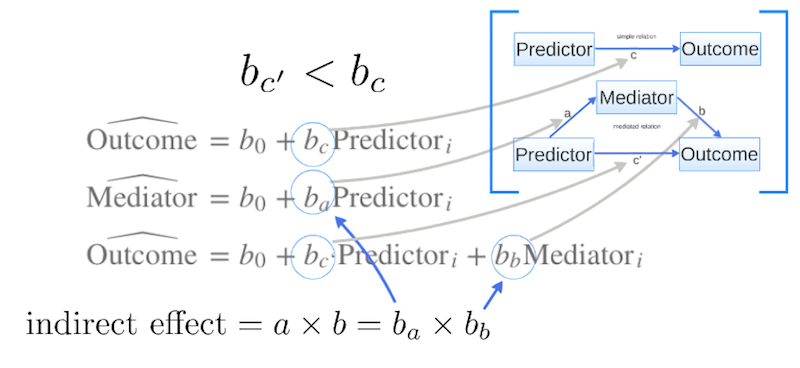
Mediation Path

The data

Apply 3 models

• Model 1
• Model 2
• Model 3

\[\widehat{\text{Outcome}} = b_0 + b_c \times \text{Predictor}_i\]

	Dependent variable
Predictors	Estimates	CI	p
(Intercept)	12.48	9.71 – 15.24	<0.001
use homeopathic remedies	4.76	4.48 – 5.04	<0.001
Observations	100
R2 / R2 adjusted	0.922 / 0.921

\[\widehat{\text{Mediator}} = b_0 + b_a \times \text{Predictor}_i\]

	Dependent variable
Predictors	Estimates	CI	p
(Intercept)	1.87	1.12 – 2.61	<0.001
use homeopathic remedies	1.21	1.14 – 1.29	<0.001
Observations	100
R2 / R2 adjusted	0.913 / 0.912

\[\widehat{\text{Outcome}} = b_0 + b_{c`} \times \text{Predictor}_i + b_b \times \text{Mediator}_i\]

	Dependent variable
Predictors	Estimates	CI	p
(Intercept)	7.14	5.15 – 9.12	<0.001
use homeopathic remedies	1.30	0.70 – 1.91	<0.001
healthy lifestyle	2.86	2.38 – 3.34	<0.001
Observations	100
R2 / R2 adjusted	0.968 / 0.968

Extract beta coëfficients

\[ \begin{aligned} b_a &= 1.21 \\ b_b &= 2.86 \\ b_c &= 4.762 \\ b_{c`} &= 1.301 \\ \end{aligned} \]

Path model

Visual

3D Visual

Interactive, give it a spin.

Indirect effect

\(a \times b = b_a \times b_b\)

b.a*b.b

use.homeopathic.remedies 
                3.461192 

b.c - b.c.accent

use.homeopathic.remedies 
                3.461192 

Indirect effect (partially standardized)

\(\frac{ab}{s_{Outcome}} = \frac{b_a b_b}{s_{Outcome}}\)

b.a*b.b/sd(speed.of.healing)

use.homeopathic.remedies 
               0.3833868 

Indirect effect (standardized)

\(\frac{ab}{s_{Outcome}} \times s_{Predictor} = \frac{b_a b_b}{s_{Outcome}} \times s_{Predictor}\)

b.a*b.b/sd(speed.of.healing)*sd(use.homeopathic.remedies)

use.homeopathic.remedies 
               0.6979258 

Types of mediation

• Parallel mediation
• Serial mediation
• Combined serial and parallel mediation
• Mediation with covariates
• Combined mediation and moderation

End

Contact

• Klinkenberg
• ln.AvU@grebneknilK.S
• ShKlinkenberg

CC BY-NC-SA 4.0

References

Wikipedia. (2024). Mediation (statistics) — Wikipedia, the free encyclopedia. http://en.wikipedia.org/w/index.php?title=Mediation%20(statistics)&oldid=1200952353.