Null Hypothesis Significance Testing

Author
Affiliation

Klinkenberg

University of Amsterdam

Published

February 19, 2024

Null Hypothesis
Significance Testing

Neyman-Pearson Paradigm

Neyman - Pearson

Two hypothesis

\(H_0\)

  • Skeptical point of view
  • No effect
  • No preference
  • No Correlation
  • No difference

\(H_A\)

  • Refute Skepticism
  • Effect
  • Preference
  • Correlation
  • Difference

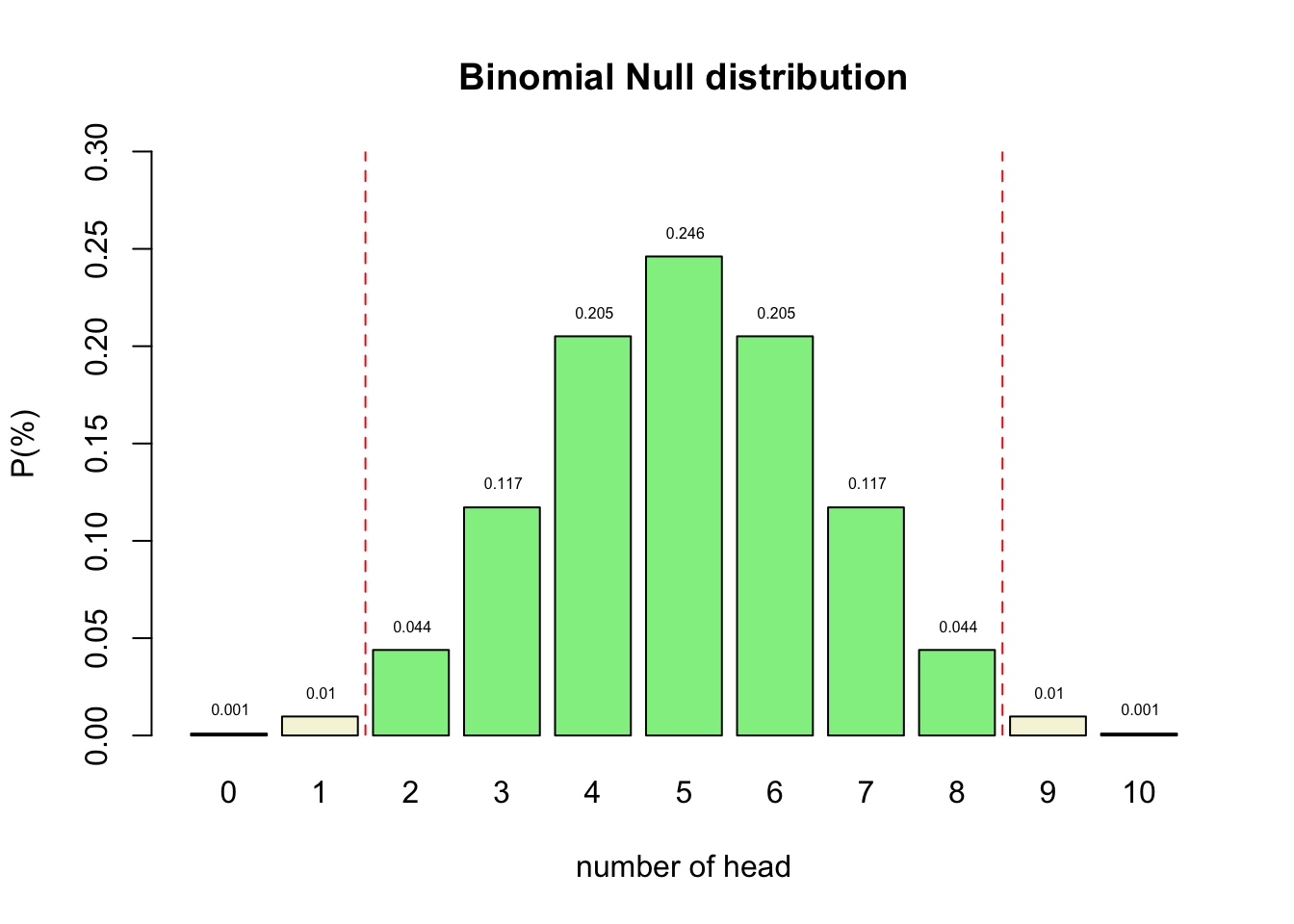
Binomial \(H_0\) distribution

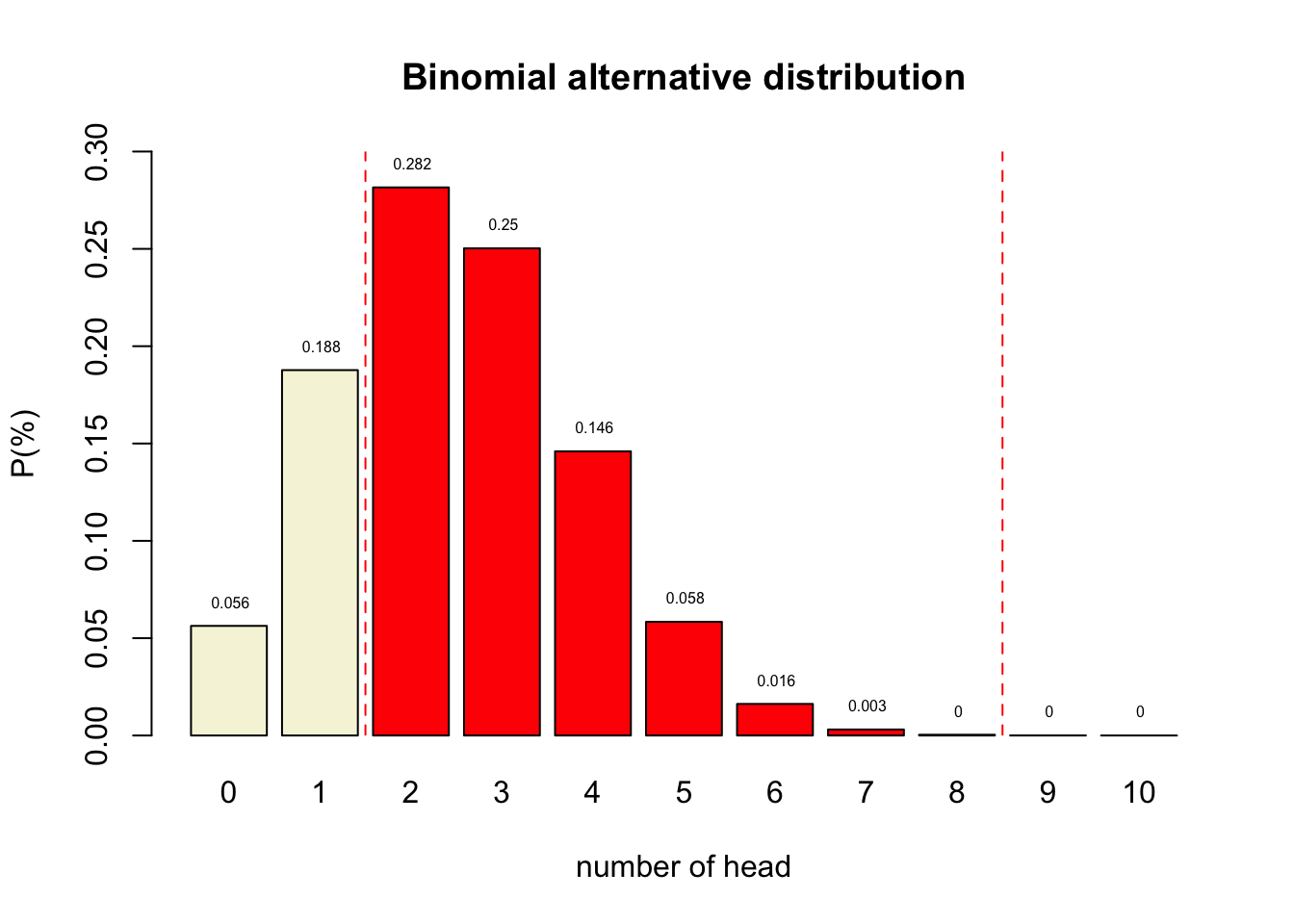
Binomial \(H_A\) distributions

Decision table

H0 = TRUE H0 = FALSE Decide to reject H0 Decide to not reject H0 Alpha α Beta β 1 - α Power 1 - β

Alpha \(\alpha\)

  • Incorrectly reject \(H_0\)
  • Type I error
  • False Positive
  • Criteria often 5%
  • Distribution depends on sample size
H0 = TRUE H0 = FALSE Decide to reject H0 Decide to not reject H0 Alpha α Beta β 1 - α Power 1 - β

Power

  • Correctly reject \(H_0\)
  • True positive
  • Power equal to: 1 - Beta
    • Beta is Type II error
  • Criteria often 80%
  • Depends on sample size
H0 = TRUE H0 = FALSE Decide to reject H0 Decide to not reject H0 Alpha α Beta β 1 - α Power 1 - β

Post-Hoc Power

  • Also known as: observed, retrospective, achieved, prospective and a priori power
  • Specificly meaning:

The power of a test assuming a population effect size equal to the observed effect size in the current sample.

O’Keefe (2007)

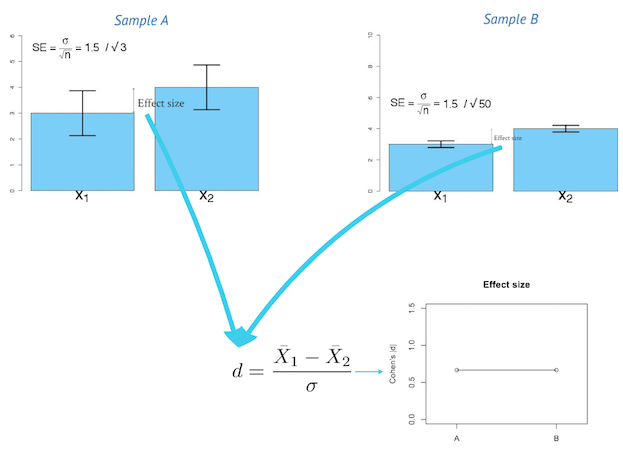
Effect size

In statistics, an effect size is a quantitative measure of the strength of a phenomenon. Examples of effect sizes are the correlation between two variables, the regression coefficient in a regression, the mean difference and standardised differences.

For each type of effect size, a larger absolute value always indicates a stronger effect. Effect sizes complement statistical hypothesis testing, and play an important role in power analyses, sample size planning, and in meta-analyses (Wikipedia, 2024).

Effect size

One minus alpha

  • Correctly accept \(H_0\)
  • True negative
H0 = TRUE H0 = FALSE Decide to reject H0 Decide to not reject H0 Alpha α Beta β 1 - α Power 1 - β

Beta

  • Incorrectly accept \(H_0\)
  • Type II error
  • False Negative
  • Criteria often 20%
  • Distribution depends on sample size
H0 = TRUE H0 = FALSE Decide to reject H0 Decide to not reject H0 Alpha α Beta β 1 - α Power 1 - β

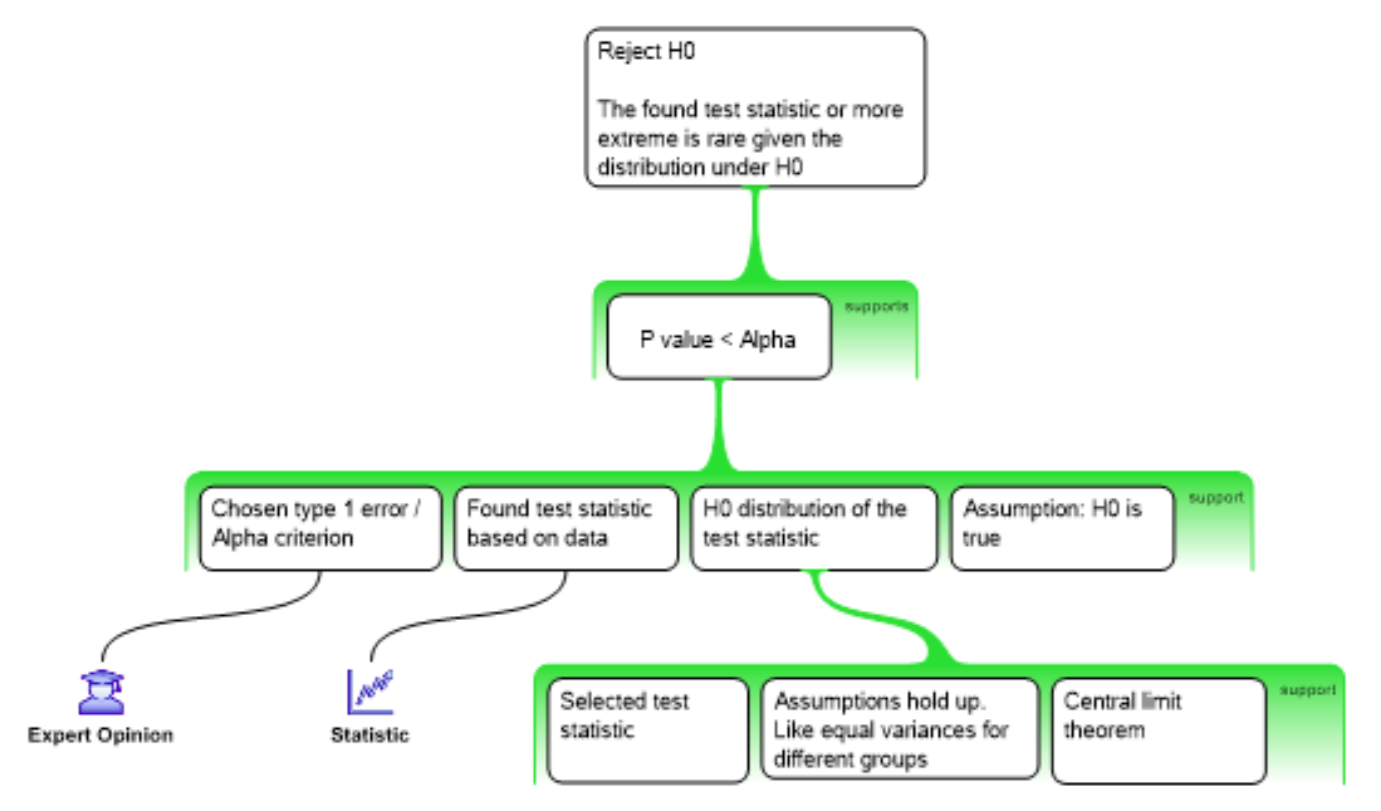
P-value

Conditional probability of the found test statistic or more extreme assuming the null hypothesis is true.

Reject \(H_0\) when:

  • \(p\)-value \(\leq\) \(alpha\)

P-value in \(H_{0}\) distribution

Test statistics

Some common test statistics

  • Number of heads
  • Sum of dice
  • Difference
  • \(t\)-statistic
  • \(F\)-statistic
  • \(\chi^2\)-statistic
  • etc…

Decision Table

Reasoning Scheme

R<-PSYCHOLOGIST

Interactive distributions app by Kristoffer Magnusson

End

Contact

CC BY-NC-SA 4.0

References

O’Keefe, D. J. (2007). Brief report: Post hoc power, observed power, a priori power, retrospective power, prospective power, achieved power: Sorting out appropriate uses of statistical power analyses. Communication Methods and Measures, 1(4), 291–299. https://doi.org/10.1080/19312450701641375
Wikipedia. (2024). Effect size — Wikipedia, the free encyclopedia. http://en.wikipedia.org/w/index.php?title=Effect%20size&oldid=1196464892.