Moderation with continuous predictors

Klinkenberg

University of Amsterdam

2024-03-11

Moderation

In statistics and regression analysis, moderation occurs when the relationship between two variables depends on a third variable. The third variable is referred to as the moderator variable or simply the moderator. The effect of a moderating variable is characterized statistically as an interaction (Wikipedia, 2024).

Model

\(\definecolor{red}{RGB}{255,0,0} \definecolor{black}{RGB}{0,0,0} \color{black}Out_i = b_0 + b_1 Pred_i + b_2 Mod_i + \color{red}b_3 Pred_i \times Mod_i \color{black}+ \epsilon_i\)

Example

Video games are among the favourite online activities for young people: two-thirds of 5–16-year-olds have their own video games console, and 88% of boys aged 8–15 own at least one games console. Although playing violent video games can enhance visuospatial acuity, visual memory, probabilistic inference, and mental rotation, compared to games such as Tetris, these games have also been linked to increased aggression in youths Another predictor of aggression and conduct problems is callous-unemotional traits such as lack of guilt, lack of empathy, and callous use of others for personal gain.

Imagine a scientist wanted to look at the relationship between playing violent video games such as Grand Theft Auto, MadWorld and Manhunt and aggression. She gathered data from 442 youths. She measured their aggressive behaviour, callous unemotional traits, and the number of hours per week they play video games (Field, 2017, sec. 11.3.1)

View data

mean centering

\(\text{pred}_\text{c} = \text{pred} - \bar{\text{pred}} = \text{pred} - 15.39\)

\(\text{mod}_\text{c} = \text{mod} - \bar{\text{mod}}= \text{mod} - 7.808\)

SPSS syntax

COMPUTE pred = pred - 15.39.
COMPUTE mod  = mod  - 7.808.
EXECUTE.

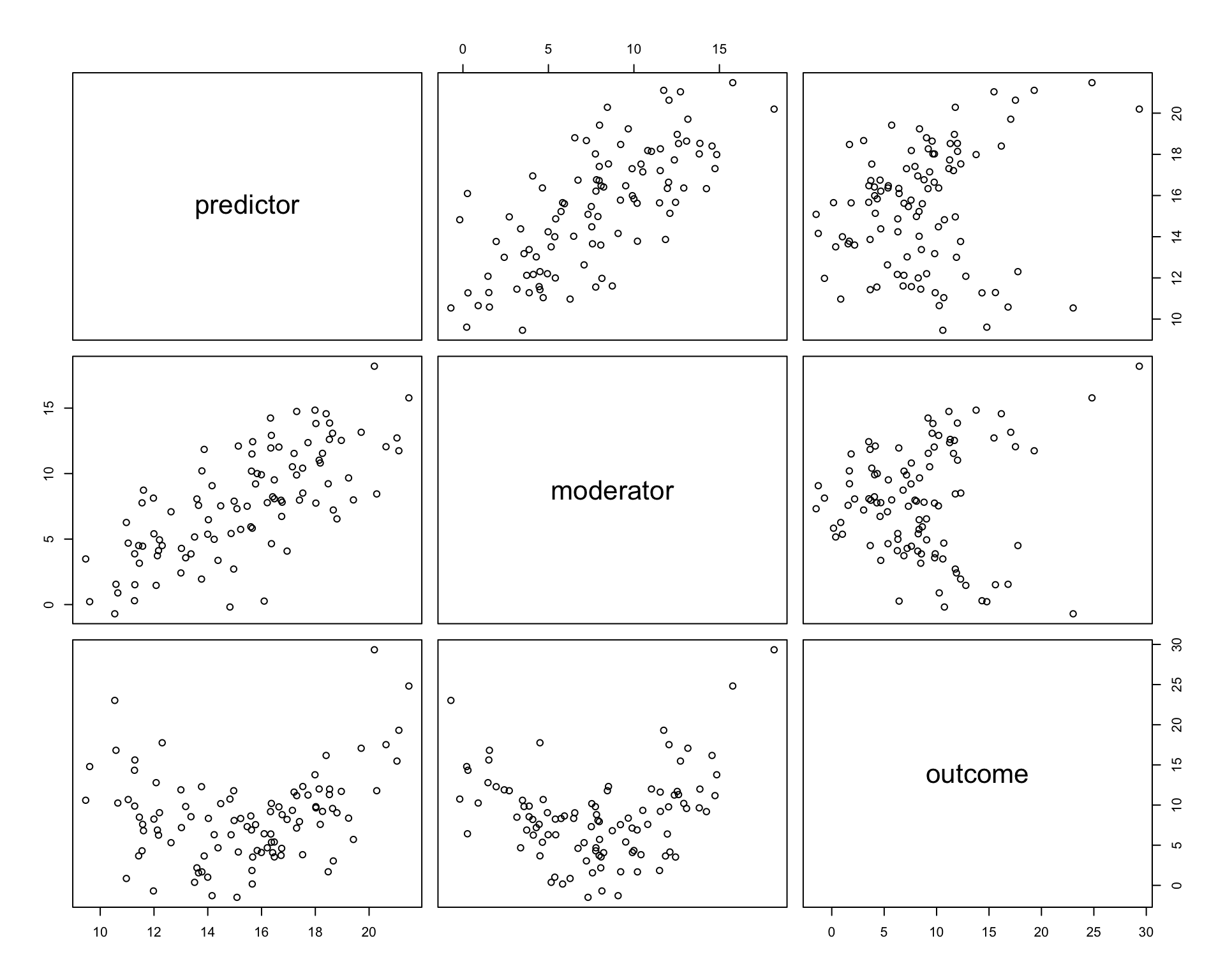
Correlations

          predictor moderator outcome
predictor     1.000     0.722   0.215
moderator     0.722     1.000   0.109
outcome       0.215     0.109   1.000

Scatterplots

3D plot

Take it for a spin (does not work on tablet)

1 SD planes

Fit model

  Dependent variable
Predictors Estimates CI p
(Intercept) 5.38 4.62 – 6.14 <0.001
predictor 0.70 0.40 – 1.01 <0.001
moderator -0.22 -0.43 – -0.00 0.050
predictor:moderator 0.37 0.32 – 0.42 <0.001
Observations 100
R2 / R2 adjusted 0.687 / 0.677

Regression equation

\(\definecolor{red}{RGB}{255,0,0} \definecolor{black}{RGB}{0,0,0} \color{black}\widehat{Out_i} = b_0 + b_1 Pred_i + b_2 Mod_i + \color{red}b_3 Pred_i \times Mod_i \color{black}\)

\(\definecolor{red}{RGB}{255,0,0} \definecolor{black}{RGB}{0,0,0} \color{black}\widehat{Out_i} = 5.38 + 0.7 \times Pred_i + -0.22 \times Mod_i + \color{red} 0.37 \times Pred_i \times Mod_i \color{black}\)

Determine slopes

To determine the slopes of the regression plane at different levels of the moderater you can add the required moderator value to the regression equation and simplify.


\(5.38 + 0.7 \times Pred + -0.22 \times Mod + 0.37 \times Pred \times Mod\)

Expected surface

Total variance

Explained variance

Variance decomposition 3D

End

Contact

CC BY-NC-SA 4.0

References

Field, A. (2017). Discovering statistics using IBM SPSS statistics, 5th edition. Retrieved from https://sussex.figshare.com/articles/book/Discovering_statistics_using_IBM_SPSS_statistics_5th_edition/23460641
Wikipedia. (2024). Moderation (statistics) — Wikipedia, the free encyclopedia. http://en.wikipedia.org/w/index.php?title=Moderation%20(statistics)&oldid=1165385148.

SMCR / SMCO