layout(matrix(c(2:6,1,1,7:8,1,1,9:13), 4, 4))
n = 56 # Sample size
df = n - 1 # Degrees of freedom
mu = 120
sigma = 15
IQ = seq(mu-45, mu+45, 1)
par(mar=c(4,2,2,0))
plot(IQ, dnorm(IQ, mean = mu, sd = sigma), type='l', col="red", main = "Population Distribution")
n.samples = 12
for(i in 1:n.samples) {
par(mar=c(2,2,2,0))
hist(rnorm(n, mu, sigma), main="Sample Distribution", cex.axis=.5, col="beige", cex.main = .75)
}T-Distribution NHST
University of Amsterdam
9/18/23
IQ next to you

http://goo.gl/T6Lo2s
Models
\[\text{outcome} = \text{model} + \text{error}\]
T-distribution
Gosset

In probability and statistics, Student’s t-distribution (or simply the t-distribution) is any member of a family of continuous probability distributions that arises when estimating the mean of a normally distributed population in situations where the sample size is small and population standard deviation is unknown.
In the English-language literature it takes its name from William Sealy Gosset’s 1908 paper in Biometrika under the pseudonym “Student”. Gosset worked at the Guinness Brewery in Dublin, Ireland, and was interested in the problems of small samples, for example the chemical properties of barley where sample sizes might be as low as 3.
Source: Wikipedia
Population distribution
Population distribution
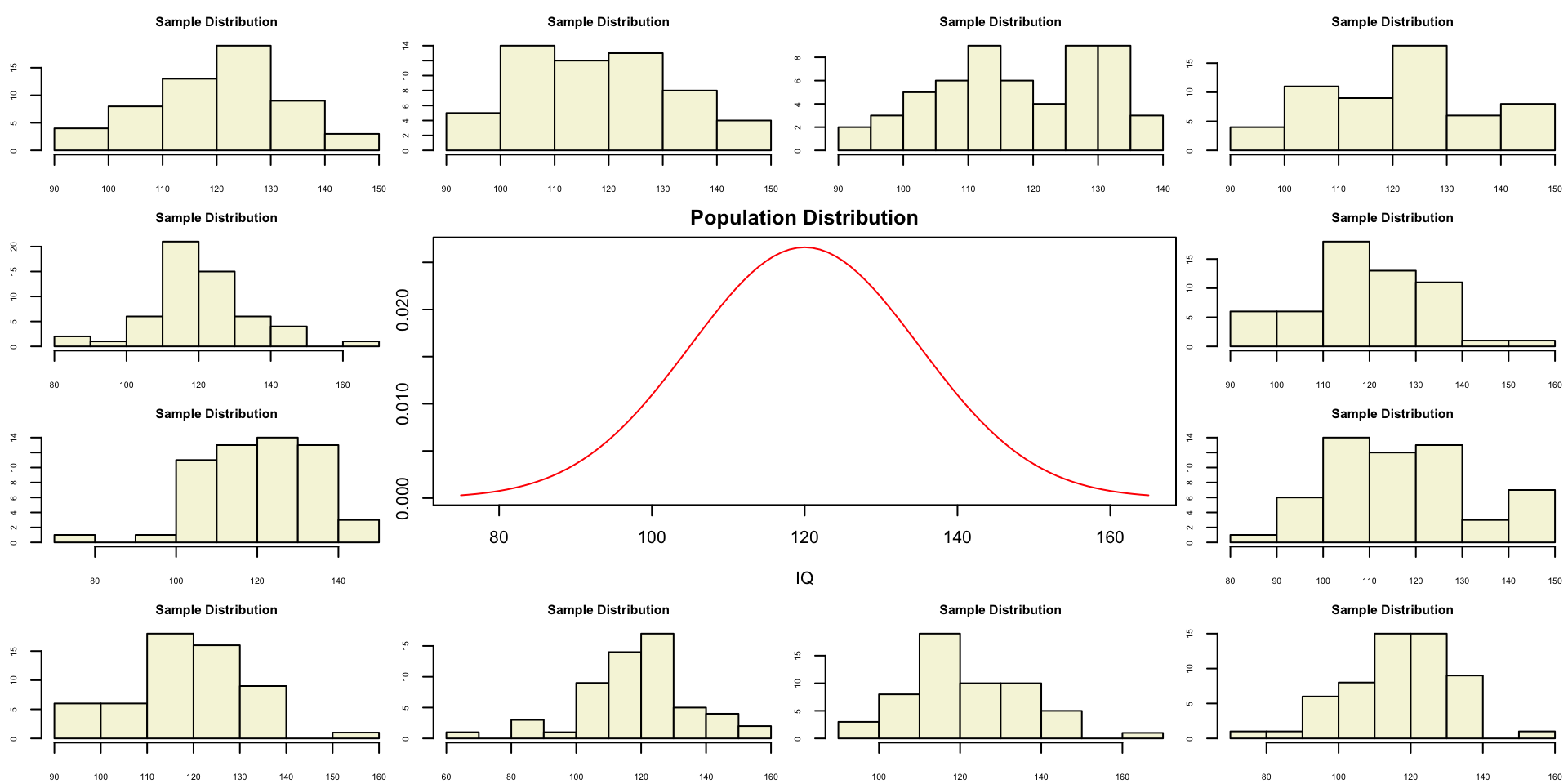
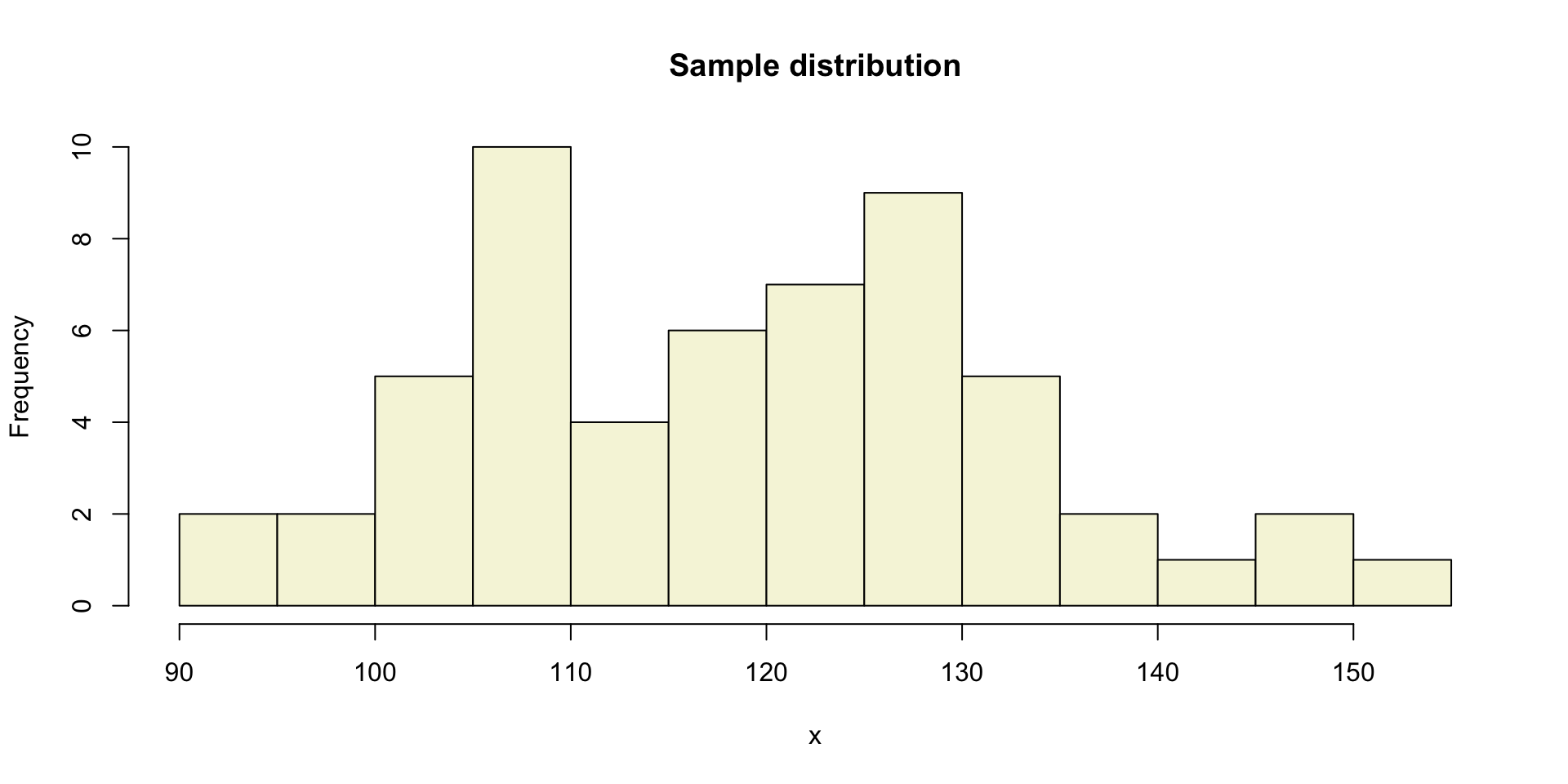
A sample
Let’s take a larger sample from our normal population.
[1] 116.28878 99.69939 108.19635 105.74030 130.17777 104.18664 118.42917
[8] 121.89237 124.29155 109.49228 113.61200 102.54243 109.95963 131.81114
[15] 103.94518 125.14939 119.12108 122.09588 126.56737 121.36213 104.44188
[22] 117.96477 137.31148 113.34714 126.40197 109.13627 109.18368 125.27857
[29] 146.92848 117.87501 129.41503 105.29906 140.71051 130.07505 110.15059
[36] 99.06620 151.84652 127.85374 135.44027 94.92003 119.92475 120.05324
[43] 109.25331 134.27541 90.69452 105.61957 133.70423 126.96402 124.77363
[50] 124.70703 111.40327 145.28843 103.62763 128.58978 125.70476 108.51775A sample
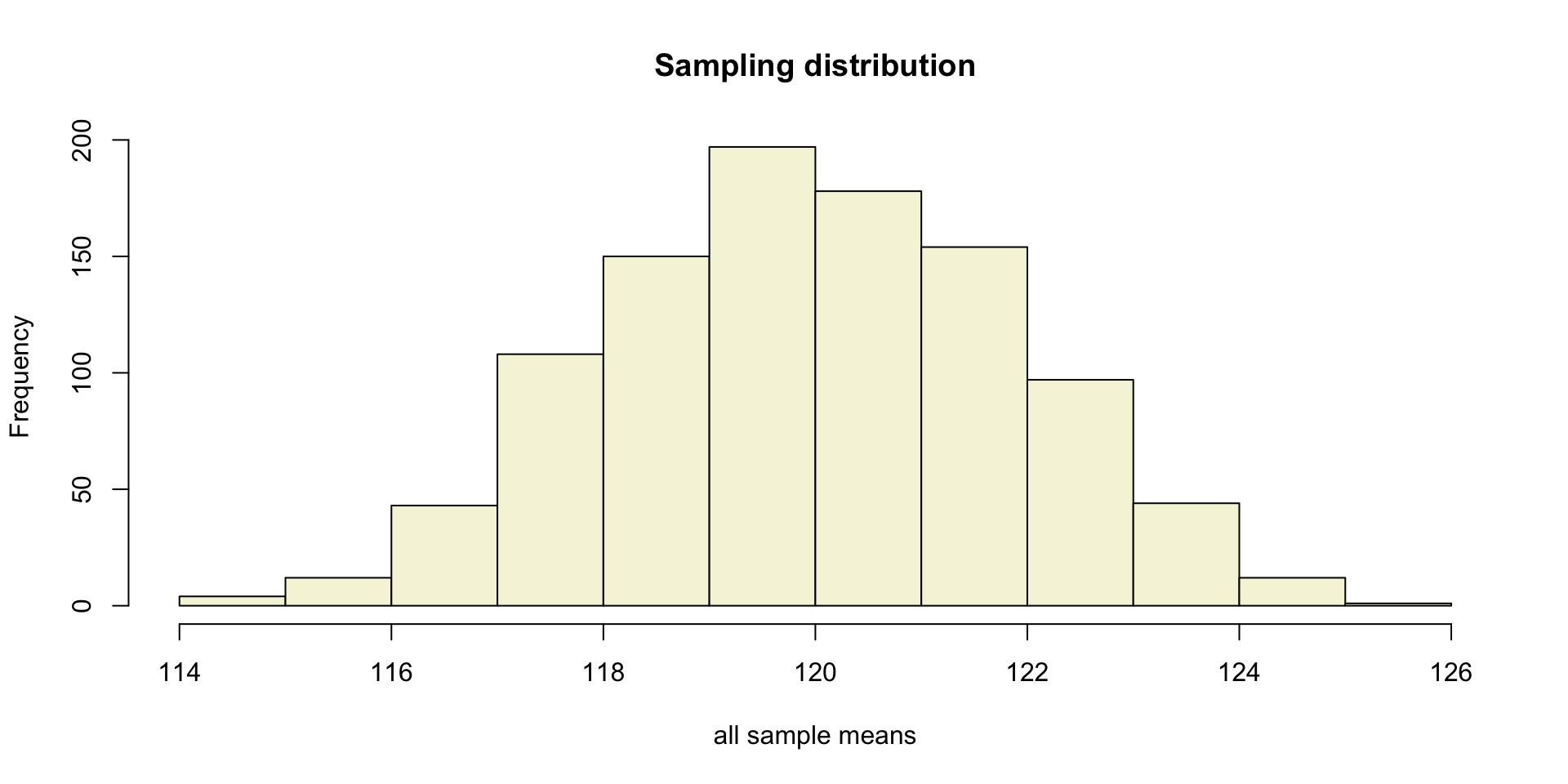
More samples
let’s take more samples.
Mean and SE for all samples
Sampling distribution
of the mean
T-statistic
\[T_{n-1} = \frac{\bar{x}-\mu}{SE_x} = \frac{\bar{x}-\mu}{s_x / \sqrt{n}}\]
So the t-statistic represents the deviation of the sample mean \(\bar{x}\) from the population mean \(\mu\), considering the sample size, expressed as the degrees of freedom \(df = n - 1\)
t-value
\[T_{n-1} = \frac{\bar{x}-\mu}{SE_x} = \frac{\bar{x}-\mu}{s_x / \sqrt{n}}\]
Calculate t-values
\[T_{n-1} = \frac{\bar{x}-\mu}{SE_x} = \frac{\bar{x}-\mu}{s_x / \sqrt{n}}\]
mean.x.values mu se.x.values t.values
[995,] 119.4718 120 2.058269 -0.2566000
[996,] 117.4671 120 1.911837 -1.3248763
[997,] 118.1724 120 1.642246 -1.1128669
[998,] 122.1121 120 2.178164 0.9696768
[999,] 118.4718 120 1.871107 -0.8167130
[1000,] 119.5706 120 2.225580 -0.1929402Sampling distribution t-values
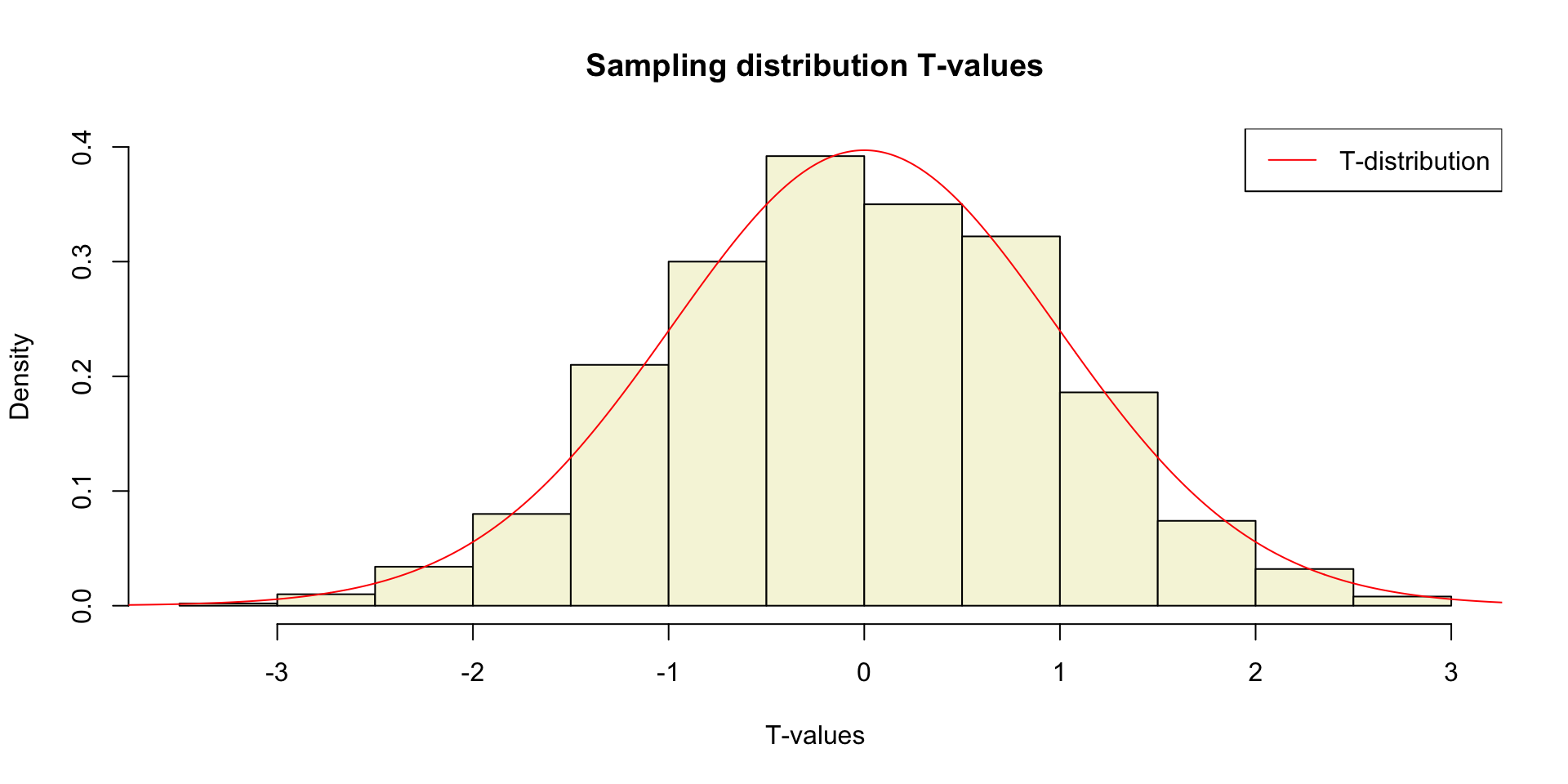
T-distribution
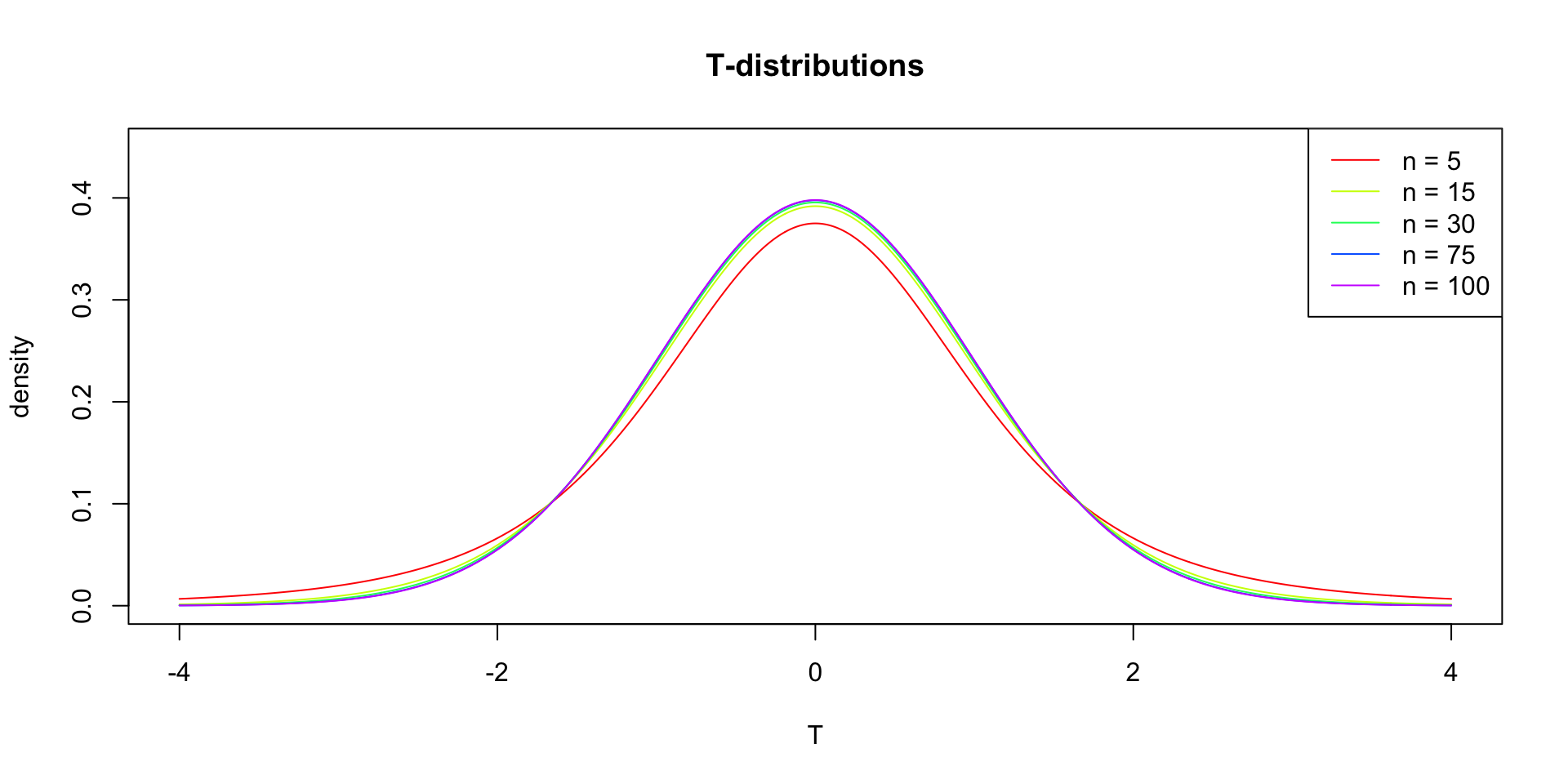
So if the population is normaly distributed (assumption of normality) the t-distribution represents the deviation of sample means from the population mean (\(\mu\)), given a certain sample size (\(df = n - 1\)).
The t-distibution therefore is different for different sample sizes and converges to a standard normal distribution if sample size is large enough.
The t-distribution is defined by:
\[\textstyle\frac{\Gamma \left(\frac{\nu+1}{2} \right)} {\sqrt{\nu\pi}\,\Gamma \left(\frac{\nu}{2} \right)} \left(1+\frac{x^2}{\nu} \right)^{-\frac{\nu+1}{2}}\!\]
where \(\nu\) is the number of degrees of freedom and \(\Gamma\) is the gamma function.
Source: wikipedia
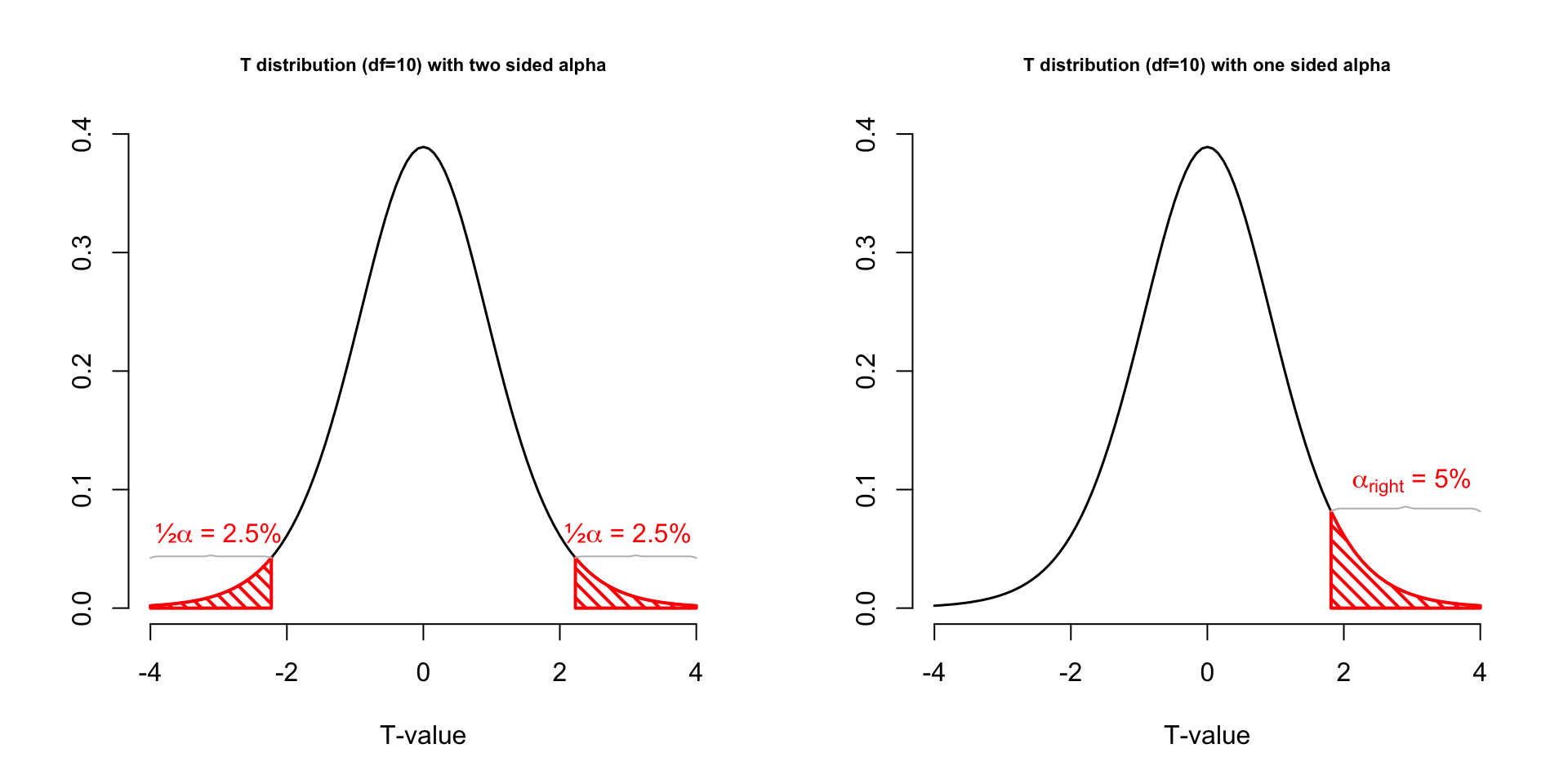
One or two sided
Two sided
- \(H_A: \bar{x} \neq \mu\)
One sided
- \(H_A: \bar{x} > \mu\)
- \(H_A: \bar{x} < \mu\)
Effect-size
The effect-size is the standardised difference between the mean and the expected \(\mu\). In the t-test effect-size is expressed as \(r\).
\[ d_\text{one-sample} = \frac{M - \mu_0}{SD}\]
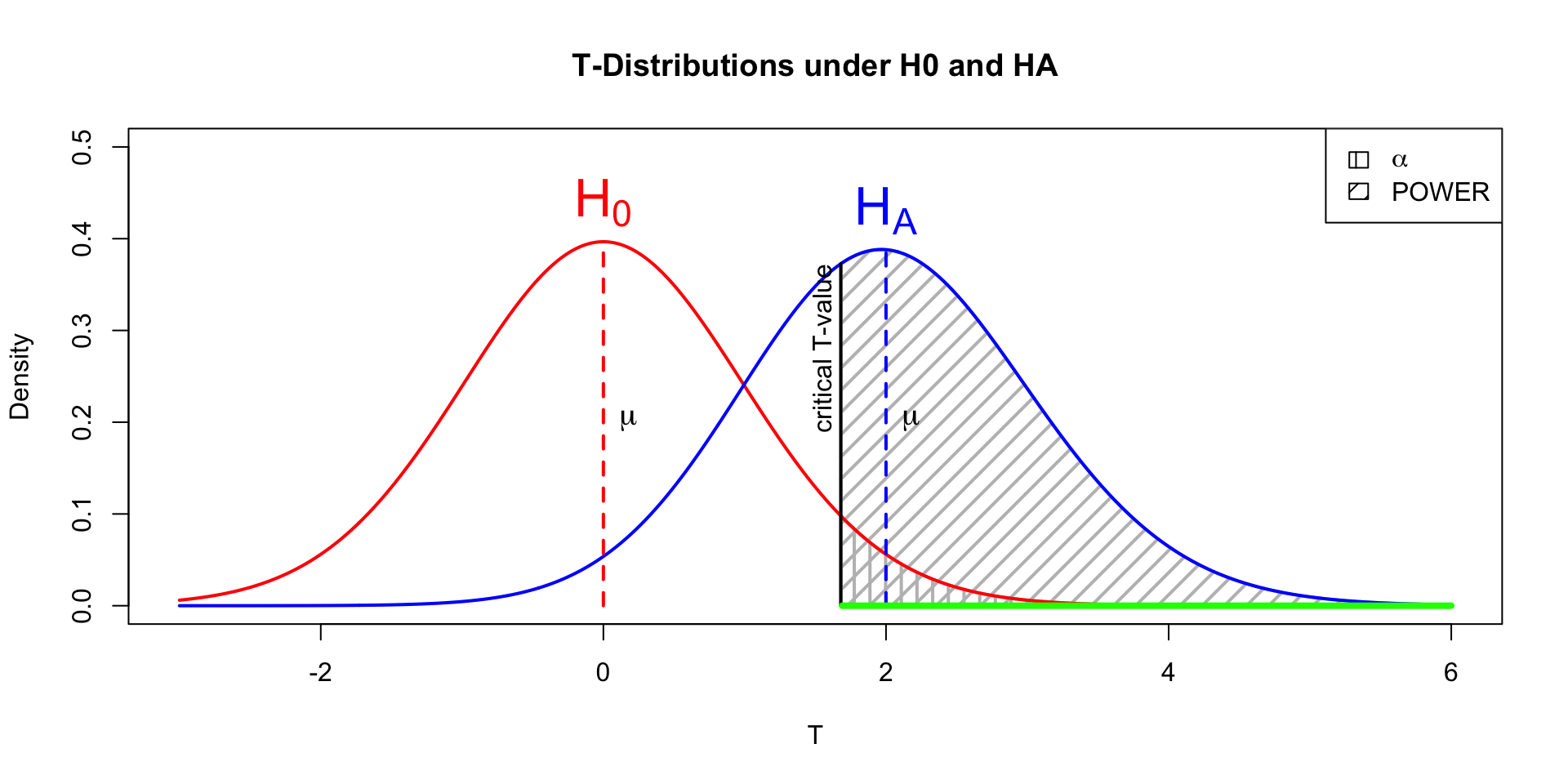
Power
- Strive for 80%
- Based on known effect size
- Calculate number of subjects needed
- Use G*Power to calculate
Alpha Power
One-sample t-test
Our data
Descriptives
\(\bar{x} = 119.75\)
\(s_x = 16.37\)
\(n = 111\)
Does this mean, differ significantly from the population mean \(\mu = 120\)?
Hypothesis
Null hypothesis
- \(H_0: \bar{x} = \mu\)
Alternative hypothesis
- \(H_A: \bar{x} \neq \mu\)
- \(H_A: \bar{x} > \mu\)
- \(H_A: \bar{x} < \mu\)
T-statistic
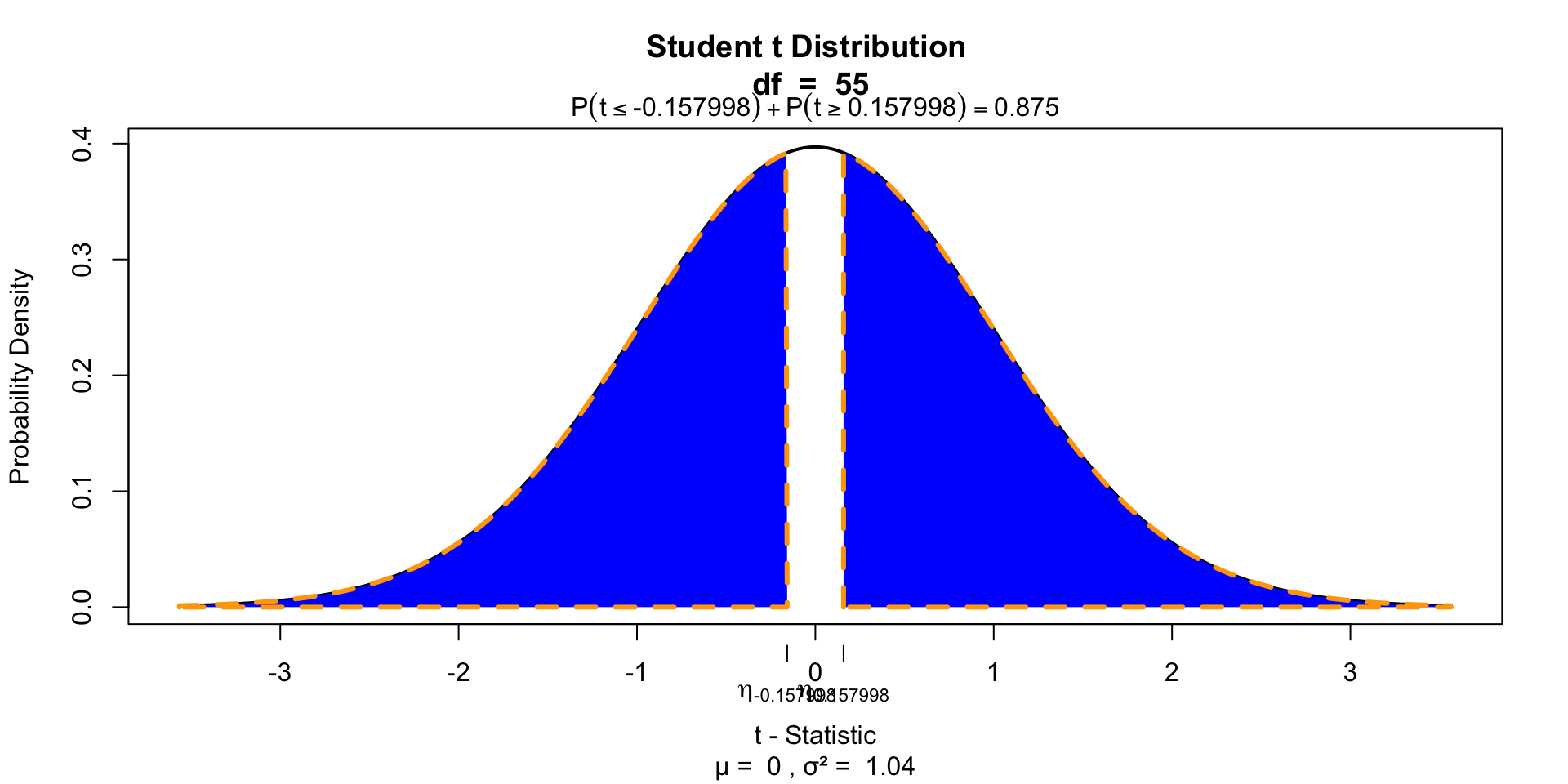
\[T_{n-1} = \frac{\bar{x}-\mu}{SE_x} = \frac{\bar{x}-\mu}{s_x / \sqrt{n}} = \frac{119.75 - 120 }{16.37 / \sqrt{111}}\]
The t-statistic represents the deviation of the sample mean \(\bar{x}\) from the population mean \(\mu\), considering the sample size.
\[t = -0.157998\]
Type I error
To determine if this t-value significantly differs from the population mean we have to specify a type I error that we are willing to make.
- Type I error / \(\alpha\) = .05
P-value one sided
Finally we have to calculate our p-value for which we need the degrees of freedom \(df = n - 1\) to determine the shape of the t-distribution.
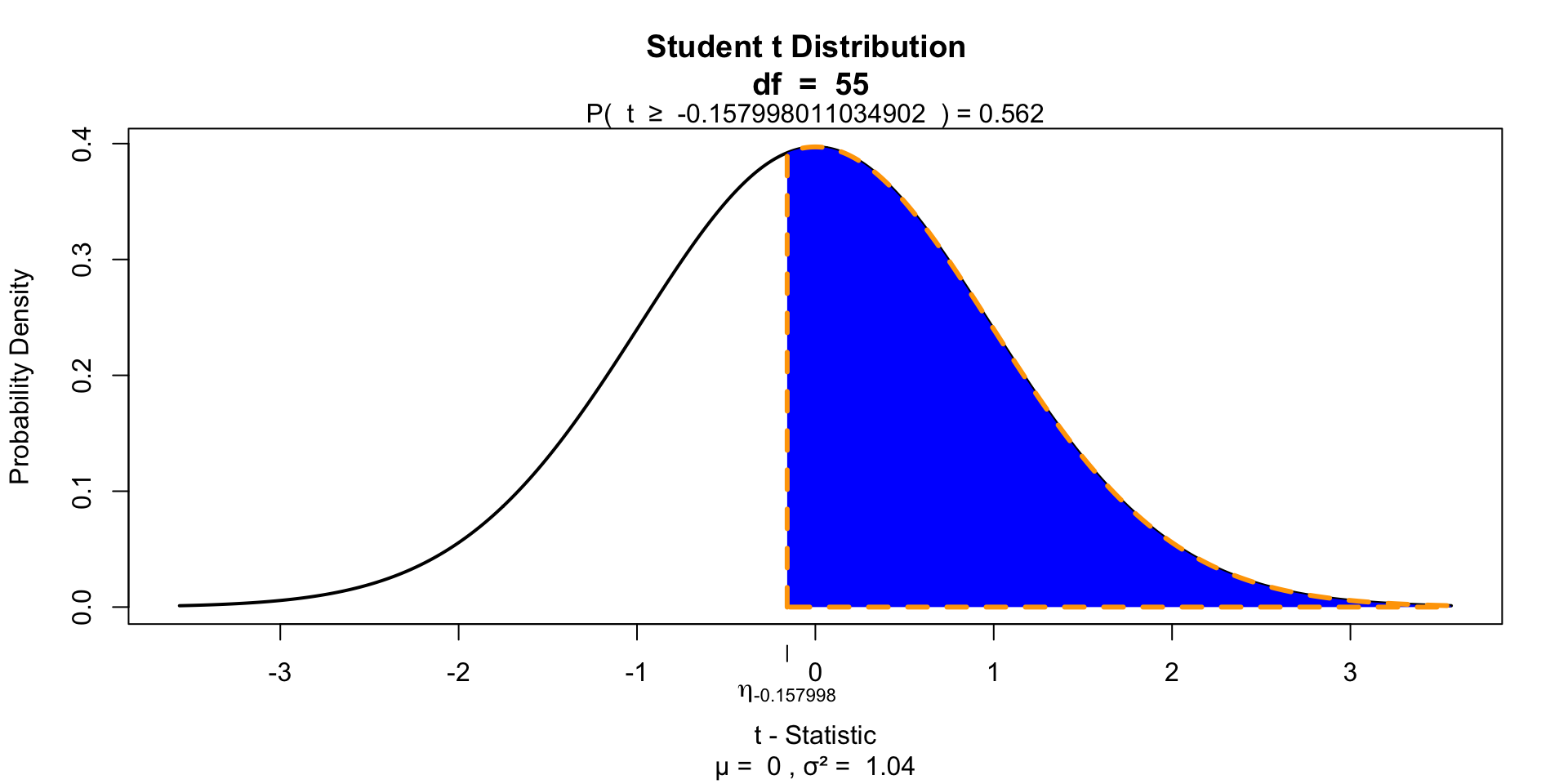
P-value two sided
End
Contact

SMCR / SMCO
