Statistical Reasoning

Null Hypothesis Testisn

Klinkenberg

University of Amsterdam

9/6/23

Course structure

Course parts

  • Lectures: On campus / Online / Video recording
  • Preparatory Assignment: Submit in Testvision and Reflection in canvas
  • Tutorials: For your support and inclass assessment
  • Exam: Knowledge and skills

Grading

\[\text{Final grade} = 0.9 \times \text{exam grade} + 0.1 \times \text{credit points}\]

  • Exam
  • Credits for
    • Tutorial participation
    • Preparatory assignment

Credits

You get 10 at the start of the course.

Number of times missed Deduction for TU Deduction for PA
1x 0 0
2x 0 2
3x 2 3
4x 4 4
5x or more 5 5

See canvas for all the details.

Learning

Reasoning in statistics

Source: ARTIST

Statistical Literacy

  • Knowledge (Basic understanding of concepts)
    • Identify
    • Describe
  • Skils (Ability to work with statistical tools)
    • Translate
    • Interpret
    • Read
    • Compute

Statistical Reasoning

  • Understanding
    • Explain why
    • Explain how

Statistical thinking

  • Apply
    • What methods to use in a specific situation
  • Critique
    • Comment and reflect on work of others
  • Evaluate
    • Assigning value to work
  • Generalize
    • What does variation mean in the large scheme of life

Empirical Cycle

By Adriaan de Groot

The components

  • Observation
    • Idea for hypothesis
  • Induction
    • General rule
    • Hypothesis
  • Deduction
    • Expectation / Prediction
    • Operationalization
  • Testing
    • Test hypothesis
    • Compare data to prediction
  • Evaluation
    • Interpret results in terms of hypothesis

Explained by Annemarie Zandscholten

Experiment

Video registration

Heads

bit.ly/2j54A2U

Emperical Cycle

  • Observation Patiënt is showing post traumatic symptoms
  • Induction Can we diagnose PTSD
  • Deduction \(H_0\): P: fair coin → C: patiënt is balanced
  • Deduction \(H_A\): P: Unfair coin → C: patiënt is unbalanced
  • Deduction \(H_A\): P: data \(\neq\) EV → C: is unbalanced
  • Testing Choose \(\alpha\) and Power
  • Evaluation Make a decision

Null distribution

Let’s analyse the null distribution of the results.

Google sheet

Distributions

What is the difference between

  • Population distribution
  • Sample distribution
  • Sampling distribution

Binomial distribution

\[ {n\choose k}p^k(1-p)^{n-k}\]

\[ {n\choose k} = \frac{n!}{k!(n-k)!} \]

With values:

n = 10   # Sample size
k = 0:10 # Discrete probability space
p = .5   # Probability of head

Probabilities

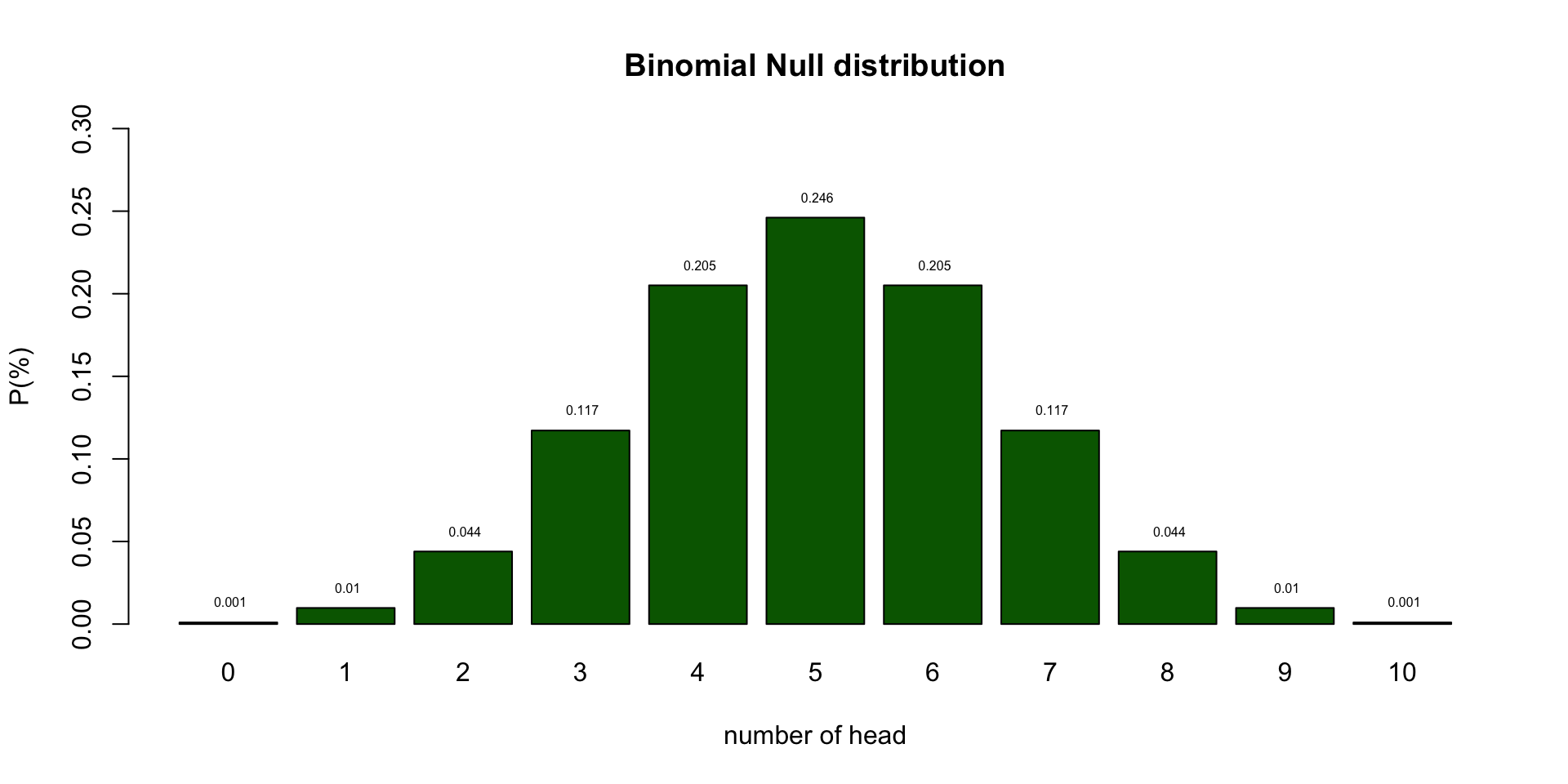
Testing

I landed 2 times head. Can we conclude PTSD?

  • As you can see from the distribution of healthy coins, we cannot conclude that by definition.
  • What we can do is indicate how rare 2 is in a healthy population.

Testing

  • Based on the null distribution we can see that the expected value (EV is 5.)
  • We can now define the \(H_0\) hypothesis: \(H_0 = 5\)
  • What is the alternative hypothesis?
  • The alternative hypothesis describes a situation where PTSD is pressent.
  • We could say that the alternative hypothesis is not 5.
    • \(H_A \ne 5\)
  • We could also formulate our \(H_0\) and \(H_A\) more abstract:
    • \(H_0:\) the patient is balenced
    • \(H_A:\) the patient is unbalenced
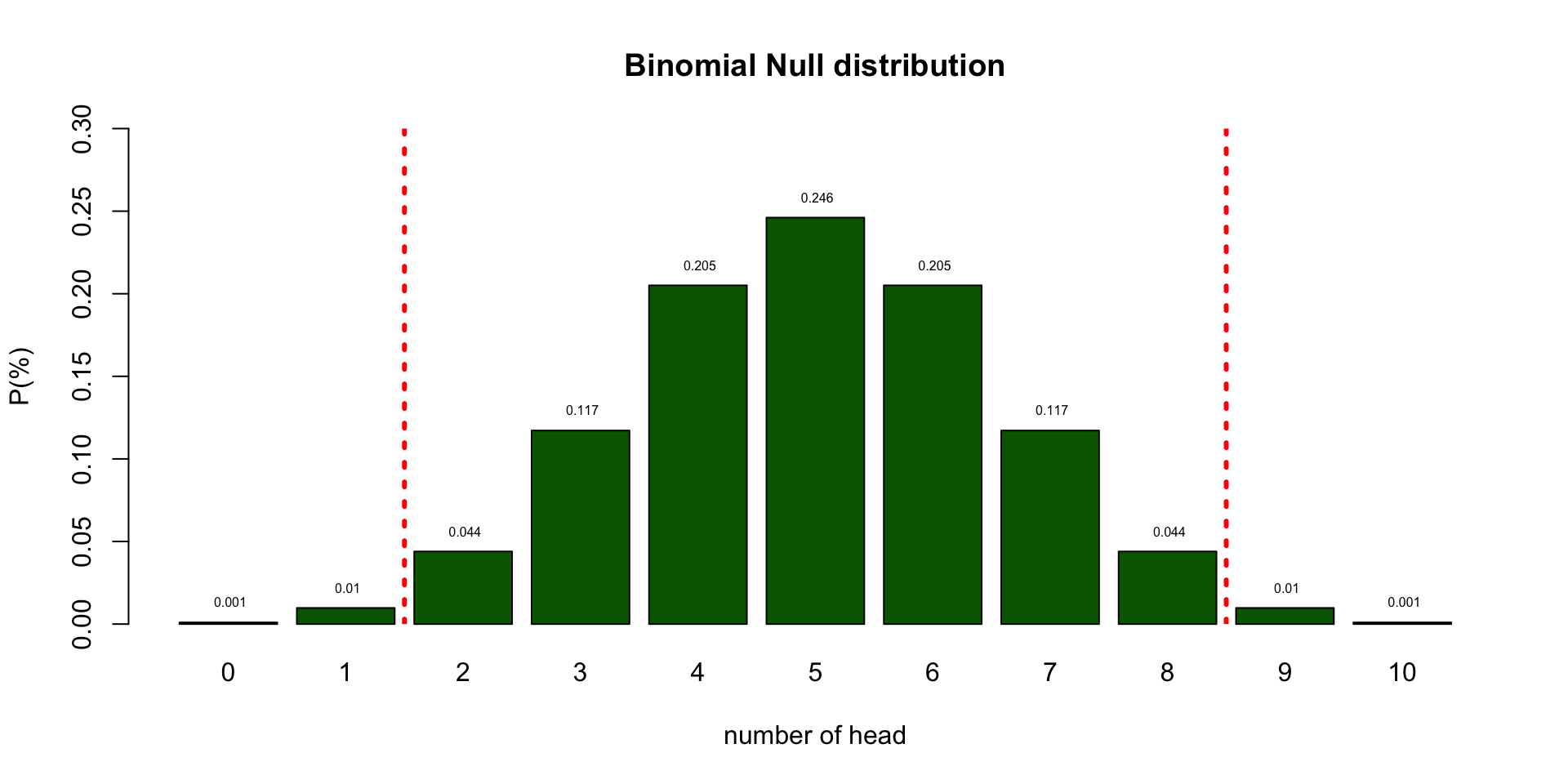
  • What criterium should we use to conclude that one would be unbalenced?
  • In the social sciences this \(\alpha\) criteria is often 5%.
  • I tossed 2 times head. That is more frequent than 5%.
  • Therefore, we conclude that our patient is probably healthy but we can never be sure.
  • My coin could still be part of the unbalenced population.

Null distribution

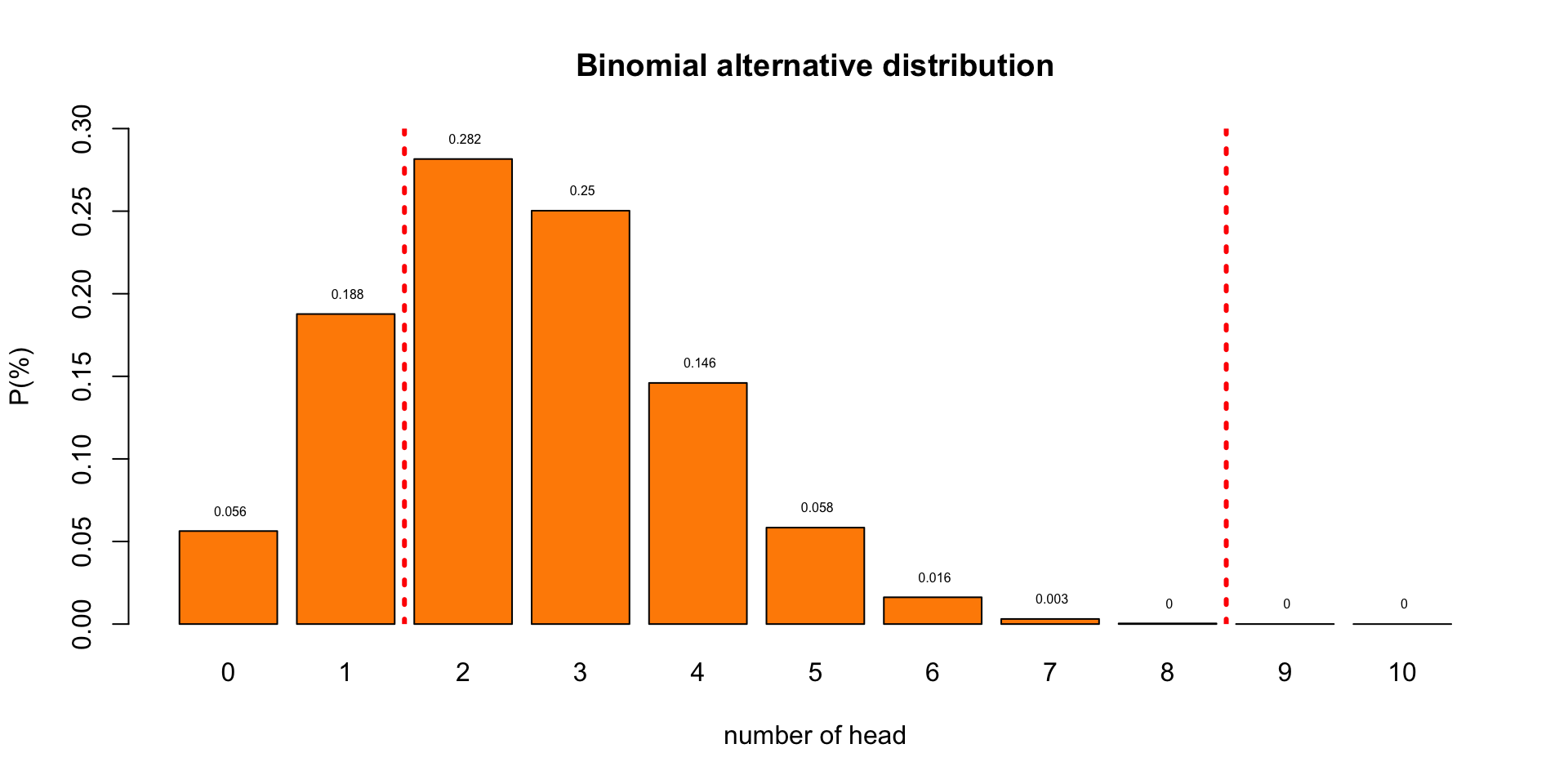
Alternative Distribution

But we have no clue of what this distribution could look like.

For now let’s assume the probability of landing heads for my coin is .25

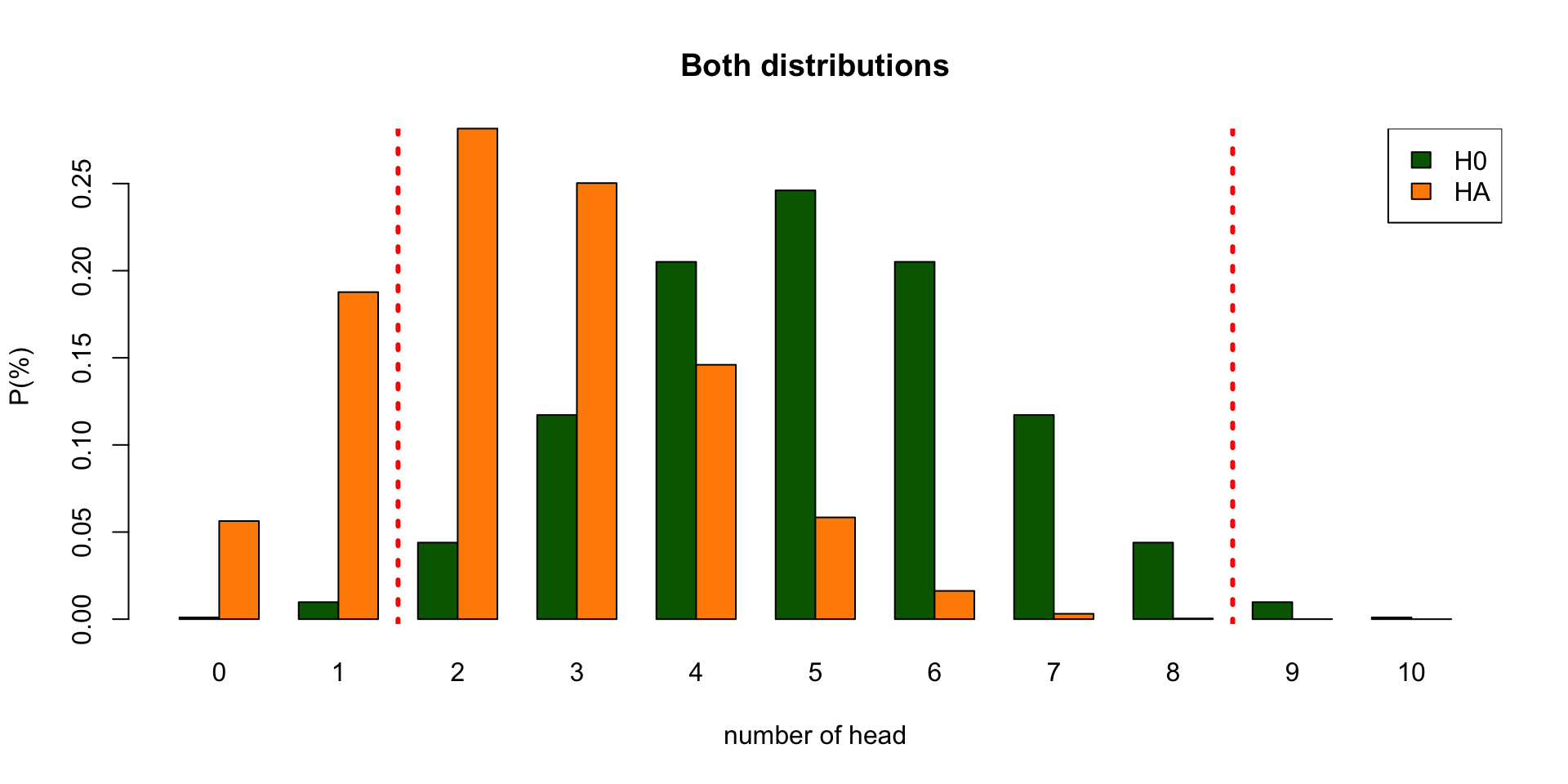
\(H_0\) and \(H_A\) distribution

End

Contact

CC BY-NC-SA 4.0

SMCR / SMCO