Mediation
Klinkenberg
16 nov 2021
Mediation
Mediation

In statistics, a mediation model is one that seeks to identify and explain the mechanism or process that underlies an observed relationship between an independent variable and a dependent variable via the inclusion of a third hypothetical variable, known as a mediator variable (also a mediating variable, intermediary variable, or intervening variable).
Source: WIKIPEDIA
Example
Does the speed of recovery after sickness improve with the use of alternative medicine or is this effect mediated by a healthy lifestyle?
Mediaton paths
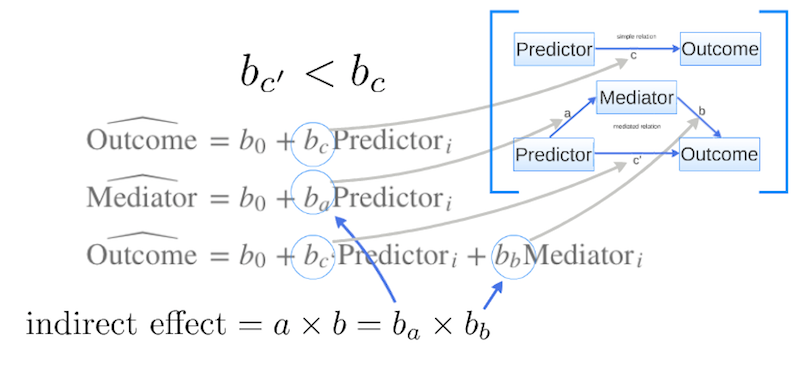
Mediation Path
Simulate data
Create predictor variable
set.seed(1976)
## Set parameters for simulation
n = 100
mu = 10
sigma = 2
## Predictor
use.homeopathic.remedies = rnorm(n, mu, sigma)Mediator
Create mediator
b0 = 2
b1 = 1.2
error = rnorm(n,0,.7)
healthy.lifestyle = b0 + b1*use.homeopathic.remedies + errorSpecify model
Create outcome variable
b0 = 6
b1 = 1.2
b2 = 3
error = rnorm(n,0,1.4)
speed.of.healing = b0 + b1*use.homeopathic.remedies + b2*healthy.lifestyle + error
data <- data.frame(use.homeopathic.remedies,
healthy.lifestyle,
speed.of.healing)
data <- round(data, 4)The data
Apply 3 models
m.1.out.pre <- lm(speed.of.healing ~ use.homeopathic.remedies)
m.2.med.pre <- lm(healthy.lifestyle ~ use.homeopathic.remedies)
m.3.out.pre.med <- lm(speed.of.healing ~ use.homeopathic.remedies + healthy.lifestyle)Extract beta coëfficients
b.a = m.2.med.pre$coefficients[2]
b.b = m.3.out.pre.med$coefficients[3]
b.c = m.1.out.pre$coefficients[2]
b.c.accent = m.3.out.pre.med$coefficients[2]View beta coëfficients
b.a## use.homeopathic.remedies
## 1.210308b.b## healthy.lifestyle
## 2.859761View beta coëfficients
b.c## use.homeopathic.remedies
## 4.762102b.c.accent## use.homeopathic.remedies
## 1.30091Visual
plot(data$use.homeopathic.remedies, data$speed.of.healing, col = 'red', xlab="alter", ylab="rocov")
fit.1 <- lm(speed.of.healing ~ use.homeopathic.remedies, data)
abline(fit.1, col = 'green')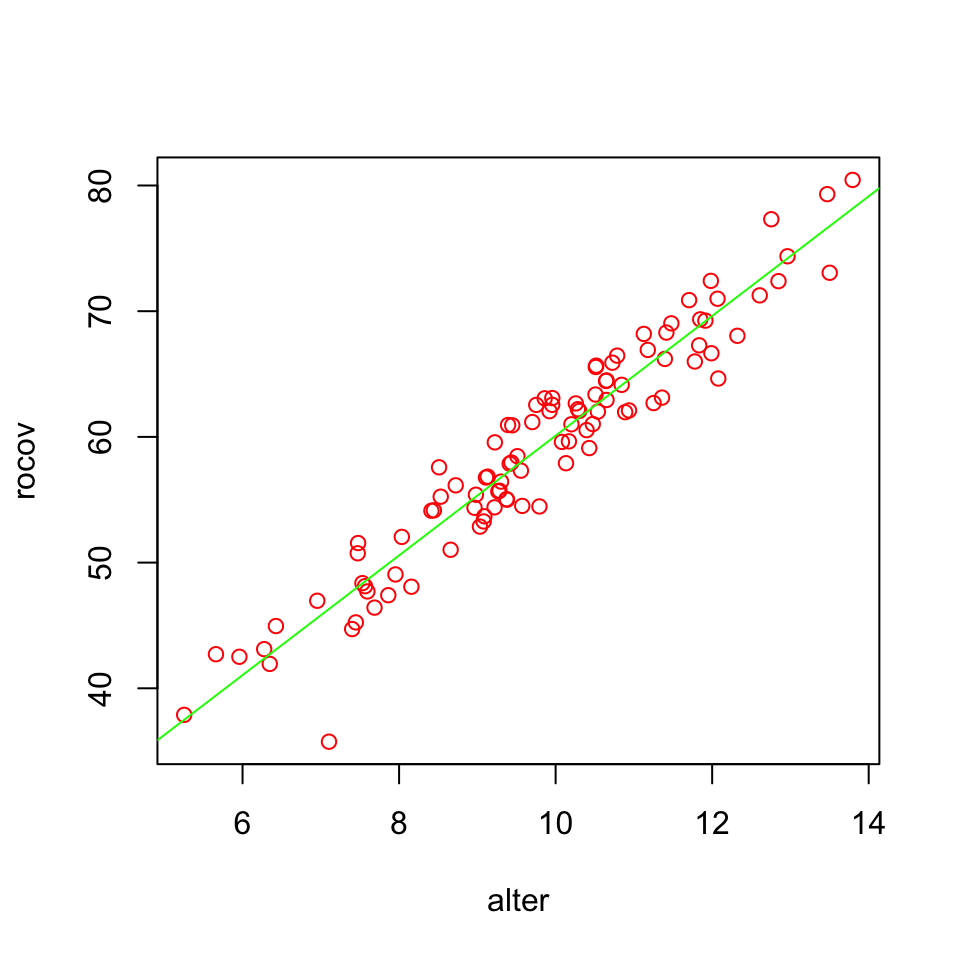
3D Visual
Interactive, give it a spin.
Calculate indirect effect
\[a \times b = b_a \times b_b\]
b.a*b.b## use.homeopathic.remedies
## 3.461192b.c - b.c.accent## use.homeopathic.remedies
## 3.461192Calculate indirect effect (partially standardized)
\[\frac{ab}{s_{Outcome}} = \frac{b_a b_b}{s_{Outcome}}\]
b.a*b.b/sd(speed.of.healing)## use.homeopathic.remedies
## 0.3833868Calculate indirect effect (standardized)
\[\frac{ab}{s_{Outcome}} \times s_{Predictor} = \frac{b_a b_b}{s_{Outcome}} \times s_{Predictor}\]
b.a*b.b/sd(speed.of.healing)*sd(use.homeopathic.remedies)## use.homeopathic.remedies
## 0.6979258Calculate \(P_M\)
\[\frac{ab}{c} = \frac{b_a b_b}{b_c}\]
b.a*b.b/b.c## use.homeopathic.remedies
## 0.7268202Calculate \(R_M\)
\[\frac{ab}{c`} = \frac{b_a b_b}{b_{c`}}\]
b.a*b.b/b.c.accent## use.homeopathic.remedies
## 2.660593Calculate \(R^2_M\)
\[R^2_{out,med} − (R^2_{out,pre \times med} − R^2_{out,pre})\]
m.4.out.med <- lm(speed.of.healing ~ healthy.lifestyle)
R2_out.med = cor(m.4.out.med$fitted.values, speed.of.healing)^2
R2_out.pre.med = cor(m.3.out.pre.med$fitted.values, speed.of.healing)^2
R2_out.pre = cor(m.1.out.pre$fitted.values, speed.of.healing)^2
R2_out.med - (R2_out.pre.med - R2_out.pre)## [1] 0.9161054Calculate \(\kappa^2\)
PROCESS version 2.16 no longer produces Preacher and Kelley’s kappa- squared as a measure of effect size for the indirect effect. This feature in earlier releases was disabled in version 2.16 in response to a recent article by Wen and Fan (2015, Psychological Methods) pointing out computational errors in its derivation.
\[\frac{ab}{max(ab)} = \frac{b_a b_b}{max(b_a b_b)}\]
What is \(max(ab)\)?

