Multiple regression
Klinkenberg
05 nov 2020
Topics
Multiple regression
Multiple regression
\[\LARGE{\text{outcome} = \text{model} + \text{error}}\]
In statistics, linear regression is a linear approach for modeling the relationship between a scalar dependent variable y and one or more explanatory variables denoted X.
\[\LARGE{Y_i = \beta_0 + \beta_1 X_{1i} + \beta_2 X_{2i} + \dotso + \beta_n X_{ni} + \epsilon_i}\]
In linear regression, the relationships are modeled using linear predictor functions whose unknown model parameters \(\beta\)’s are estimated from the data.
Source: wikipedia
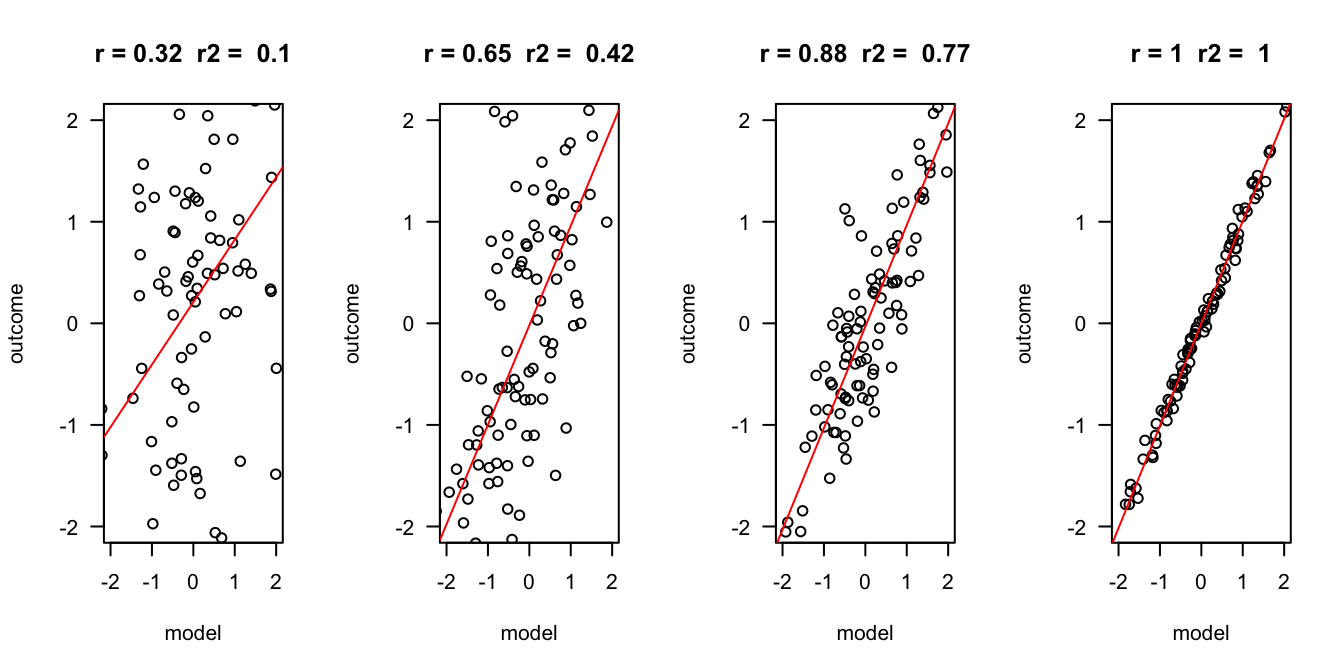
Outcome vs Model
error = c(2, 1, .5, .1)
n = 100
layout(matrix(1:4,1,4))
for(e in error) {
x = rnorm(n)
y = x + rnorm(n, 0 , e)
r = round(cor(x,y), 2)
r.2 = round(r^2, 2)
plot(x,y, las = 1, ylab = "outcome", xlab = "model", main = paste("r =", r," r2 = ", r.2), ylim=c(-2,2), xlim=c(-2,2))
fit <- lm(y ~ x)
abline(fit, col = "red")
}
Assumptions
A selection from Field (8.3.2.1. Assumptions of the linear model):
For simple regression
- Sensitivity
- Homoscedasticity
For multiple regressin
- Multicollinearity
- Linearity
Multicollinearity

To adhere to the multicollinearity assumptien, there must not be a too high linear relation between the predictor variables.
This can be assessed through:
- Correlations
- Matrix scatterplot
- VIF: max < 10, mean < 1
- Tolerance > 0.2
Linearity
For the linearity assumption to hold, the predictors must have a linear relation to the outcome variable.
This can be checked through:
- Correlations
- Matrix scatterplot with predictors and outcome variable
Example
Perdict study outcome based on IQ and motivation.
Read data
data <- read.csv('IQ.csv', header=T)
head(data)## Studieprestatie Motivatie IQ
## 1 2.710330 3.276778 129.9922
## 2 2.922617 2.598901 128.4936
## 3 1.997056 3.207279 130.2709
## 4 2.322539 2.104968 125.7457
## 5 2.162133 3.264948 128.6770
## 6 2.278899 2.217771 127.5349IQ = data$IQ
study.outcome = data$Studieprestatie
motivation = data$MotivatieRegression model in R
Perdict study outcome based on IQ and motivation.
fit <- lm(study.outcome ~ IQ + motivation)What is the model
fit$coefficients## (Intercept) IQ motivation
## -30.2822189 0.2690984 -0.6314253b.0 = round(fit$coefficients[1], 2) ## Intercept
b.1 = round(fit$coefficients[2], 2) ## Beta coefficient for IQ
b.2 = round(fit$coefficients[3], 2) ## Beta coefficient for motivationDe beta coëfficients are:
- \(b_0\) (intercept) = -30.28
- \(b_1\) = 0.27
- \(b_2\) = -0.63.
Visual
What are the expected values based on this model
\[\widehat{\text{studie prestatie}} = b_0 + b_1 \text{IQ} + b_2 \text{motivation}\]
exp.stu.prest = b.0 + b.1 * IQ + b.2 * motivation
model = exp.stu.prest\[\text{model} = \widehat{\text{studie prestatie}}\]
Apply regression model
\[\widehat{\text{studie prestatie}} = b_0 + b_1 \text{IQ} + b_2 \text{motivation}\] \[\widehat{\text{model}} = b_0 + b_1 \text{IQ} + b_2 \text{motivation}\]
cbind(model, b.0, b.1, IQ, b.2, motivation)[1:5,]## model b.0 b.1 IQ b.2 motivation
## [1,] 2.753512 -30.28 0.27 129.9922 -0.63 3.276778
## [2,] 2.775969 -30.28 0.27 128.4936 -0.63 2.598901
## [3,] 2.872561 -30.28 0.27 130.2709 -0.63 3.207279
## [4,] 2.345205 -30.28 0.27 125.7457 -0.63 2.104968
## [5,] 2.405860 -30.28 0.27 128.6770 -0.63 3.264948\[\widehat{\text{model}} = -30.28 + 0.27 \times \text{IQ} + -0.63 \times \text{motivation}\]
How far are we off?
error = study.outcome - model
cbind(model, study.outcome, error)[1:5,]## model study.outcome error
## [1,] 2.753512 2.710330 -0.04318159
## [2,] 2.775969 2.922617 0.14664823
## [3,] 2.872561 1.997056 -0.87550534
## [4,] 2.345205 2.322539 -0.02266610
## [5,] 2.405860 2.162133 -0.24372667Outcome = Model + Error
Is that true?
study.outcome == model + error## [1] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
## [19] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
## [37] TRUE TRUE TRUE
- Yes!
Visual
plot(study.outcome, xlab='personen', ylab='study.outcome')
n = length(study.outcome)
gemiddelde.study.outcome = mean(study.outcome)
## Voeg het gemiddelde toe
lines(c(1, n), rep(gemiddelde.study.outcome, 2))
## Wat is de totale variantie?
segments(1:n, study.outcome, 1:n, gemiddelde.study.outcome, col='blue')
## Wat zijn onze verwachte scores op basis van dit regressie model?
points(model, col='orange')
## Hoever zitten we ernaast, wat is de error?
segments(1:n, study.outcome, 1:n, model, col='purple', lwd=3)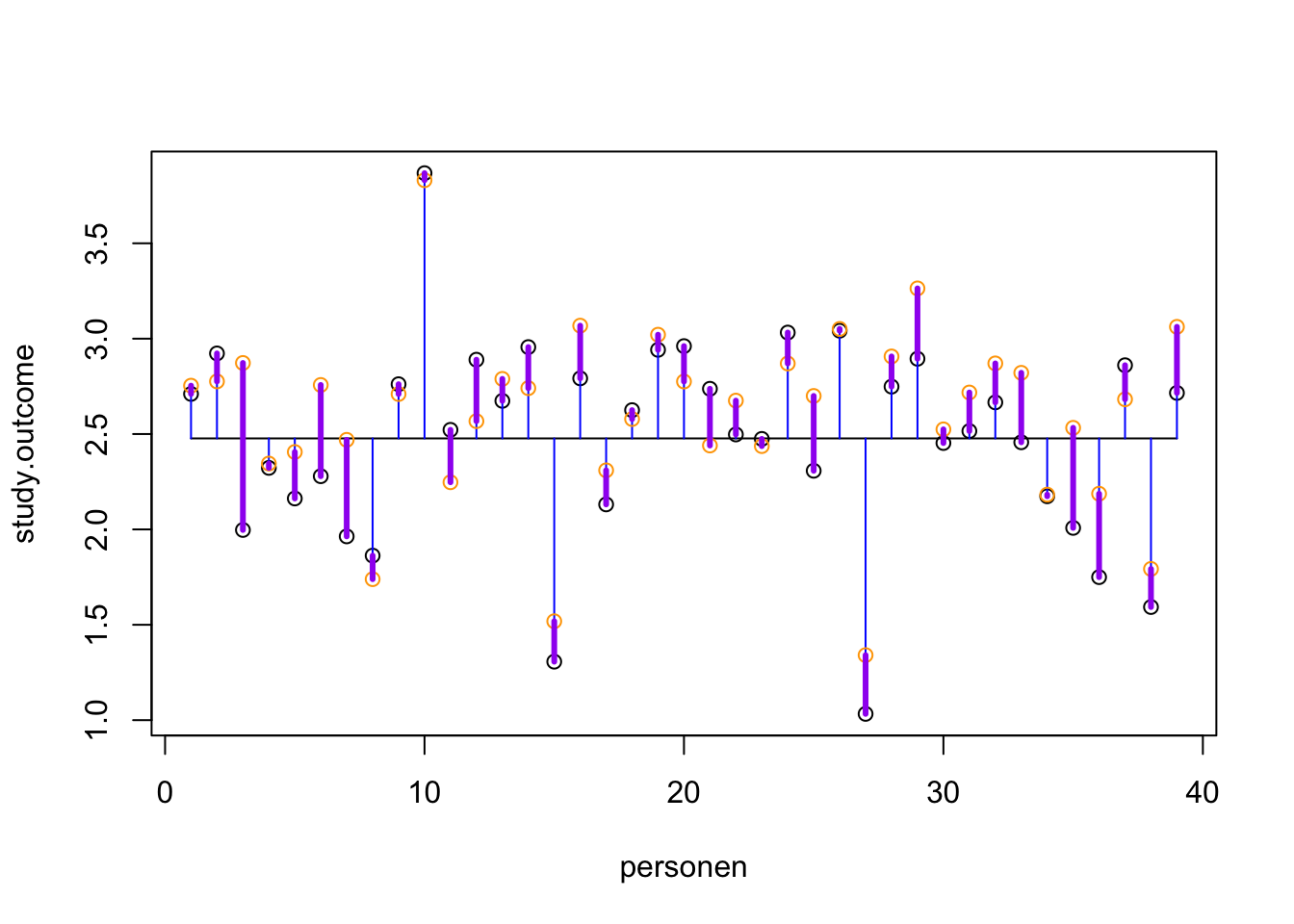
Explained variance
The explained variance is the deviation of the estimated model outcome compared to the total mean.
To get a percentage of explained variance, it must be compared to the total variance. In terms of squares:
\[\frac{{SS}_{model}}{{SS}_{total}}\]
We also call this: \(r^2\) of \(R^2\).
Why?
r = cor(study.outcome, model)
r^2## [1] 0.7527463